图的存储结构(上) 邻接矩阵和邻接表
这里写目录标题
- 邻接矩阵
-
-
- 无向图
- 有向图
- 网
- 实现代码
-
- 邻接表
-
-
- 无向图
- 有向图
- 网
- 实现代码
-
邻接矩阵
考虑到图是由顶点的边或弧两部分组成,合在一起比较困难,所以自然而然地考虑把这两个部分分开存储。
邻接矩阵存储方式使用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(或者称为邻接矩阵)存储图中的边或弧的信息。
无向图
设图G有n个顶点,则邻接矩阵是一个n×n的方阵,则有如下定义:
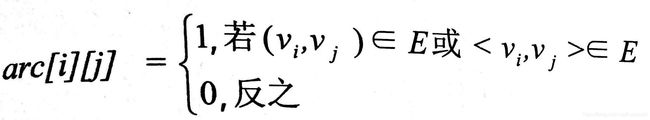
二维数组的值为0代表不存在这样的边
二维数组的值为1代表存在这样的边
下图实例中转化为邻接矩阵:
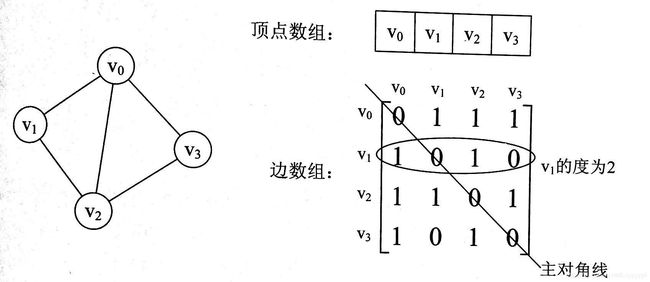
根据图中的信息可知:
1.主对角线上的值全为0,因为不存在顶点到自身的边。
2.无向图的邻接矩阵是一个对称矩阵,因为如果存在v0和v1的边,就一定会存在v0和v1的边。
3.非常容易判断两顶点间有边无边。
4.可以容易知道vi的邻接点有哪些,就是将矩阵中第i行(或第i列)元素扫描一遍,arc[i][j]=1的就是邻接点。
5.我们要知道某个顶点的度,其实就是这个顶点在邻接矩阵中第i行(或第i列)的元素之和。
有向图
有向图的定义和无向图的定义是一样的
下图实例中转化为邻接矩阵:

根据图中的信息可知:
1.有向图中的矩阵并不对称。
2.有向图中讲究出度和入度:
顶点Vi的出度为第Vi行各数之和
顶点Vi的入度为第Vi列各数之和。
3.有向图中顶点Vi的邻接点就是顶点Vi的出度点,即扫描第Vi行的各个数,arc[i][j]=1的顶点为邻接点。
网
每条边上带有权的图叫做网,所以权值就需要被存储下来,所以网的定义和图的定义有一点取别,定义如下:

注:Wij表示的某条边或弧上的权值,∞表示一个不可能的极限值,用一个不可能的值代表不存在(这也是网和图在定义上的差别)
下图实例中转化为邻接矩阵:

实现代码
邻接矩阵存储的结构:
(写代码是为了实现物理存储结构)
typedef char VertexType; //顶点类型由用户定义
typedef int EdgeType; //边上的权值类型由用户定义
#define MAX 100 //最大定点数由用户定义
#define INFINITY 65535 //用65535表示∞由用户定义
typedef struct
{
VertexType vexs[MAX]; //一维数组表示顶点表
EdgeType arc[MAX][MAX]; //二维数组表示邻接矩阵
int numVertaxes,numEdges; //表示突中当前的定点数和边数
//这个一定不能忘记
}MGraph;
有了这个结构定义,我们构造一个图其实就是个顶点表和边表输入数据的过程,我们来看看无向网图的代码:
void CreateMGraph(MGrgph *G);
{
int i,j,k,k;
printf("输入顶点数和边数:\n");
scanf("%d,%d",&G->numVertexes,&G->numEdges);
for(i=0;i<G->numVertexexes;i++)
scanf(&G->vexs[i]); //读入顶点信息,建立顶点表
for(i=0;i<numVertexexes;i++)
for(j=0;j<numVertexexes;j++)
G->arc[i][j]=INFINITY; //邻接矩阵的初始化
//所有值都调为INFINITY
for(k=0;k<G->numEdges;k++) //读入numEdges条边,建立邻接矩阵
{
printf("输入边(vi,vj)上的下标i,下标j和权值w:\n");
scanf("%d,%d,%d",&i,&j,&w);
G->arc[i][j]=w;
G->arc[j][i]=G->arc[i][j]; //因为是无向图,所以是对称矩阵
}
}
邻接表
前言:对于边数相对于顶点较少的图来说,用邻接矩阵这种存储结构对存储空间是极大的浪费。顺序存储结构存在预先分配内存而导致存储空间浪费的问题,于是我们可以考虑用链式存储结构,避免存储空间浪费的问题。
我们把数组与链表相结合的存储方法成为邻接表
无向图
邻接表的定义如下:
1.顶点表:所有顶点用一个一维数组存储,也可以用单链表存储。不过数组更容易地读取顶点信息,更加方便。在顶点数组中还需要存储指向第一个临界点的指针,便于查找该顶点的边信息。
2.边表:由于邻接点的个数不定,所以用单链表存储。无向图称为顶点Vi的边表,有向图则称为顶点Vi作为弧尾的出边表。
图中的每个顶点Vi的所有邻接点构成一个线性表,即顶点Vi的边表为一个线性表
下图表示无向图邻接表的转换:
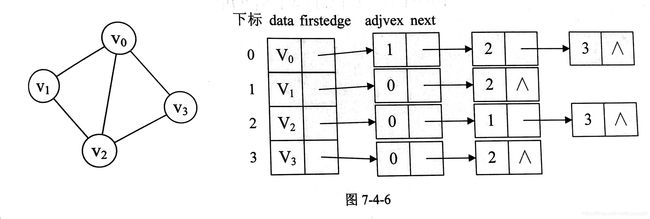
data是数据域存储顶点的信息
firstedge是指针域,指向该顶点的第一个邻接点
adjvex是邻接点域,存储该顶点的邻接点在顶点表中的下标
next是指针域,指针指向顶点的下一个邻接点
例如顶点V1与V0,V2互为邻接点,则在V1的边表中adjvex分别为0和2
根据图中信息可知:
1.很容易判断某顶点的度,即该顶点边表结点个数
2.很容易判断顶点Vi和Vj是否存在边
3.顶点的所有邻接点,需要对此顶点的边表进行遍历(因为边表是单链表需要全部遍历),得到的adjvex域对应的顶点就是邻接点
有向图
如果是有向图,邻接表的结构也是类似的,只不过是由于有向图有方向。
以顶点为弧尾来存储的边表称为邻接表,很容易得到顶点的出度
以顶点为弧头来存储的边表称为逆邻接表,很容易得到顶点的入度
下图为有向图转换为邻接表:

网
网的邻接表的定义和图的定义是类似的,只要在边表在边表结点的定义中增加一个weight的数据域来存储权值就可以了
下图为网转换为邻接表:
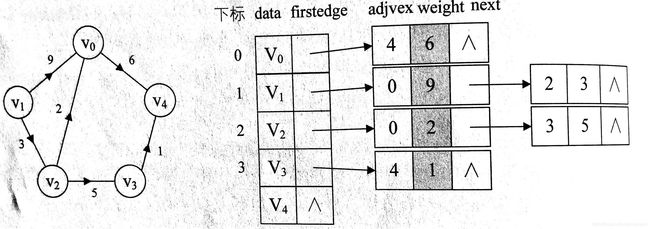
涂黑部分为增加的weight域
实现代码
结点定义的代码如下:
typedef char VertexType;
typedef int EdegeType;
#define MAX 100
typedef struct EdgeNode //边表结点
{
int adjvex;
EdegeType weight;
struct EdegeType *next; //指向下一个同这个结构的结点指针
}EdgeNode;
typedef struct VertexNode //顶点表结点
{
VertexType data;
EdegeNode *firstedge;
}VertexNode,AdjList[MAX];
typedef struct //图结构的创建
{
AdjList adjList;
int numVertexes,numEdeges; //图中当前的顶点数和边数
//一定不要忘记这个!!!
}GraphAdjList;
邻接表的创建,下面是无向图邻接表的创建:
void CreateALGraph(GraphAdjList *G)
{
int i,j,k;
EdgeNode *e;
printf("输入顶点数和边数:\n");
scanf("%d,%d",&G->numVertexes,&G->numEdeges);
for(i=0;i<G->numVertexes;i++)
{
scanf(&G->adjList.data); //输入顶点信息
G->adjList[i].firstedge=NULL; //把顶点的边表置为空表
}
for(k=0;k<G->numEdeges;k++) //建立边表
{
printf("输入边(vi,vj)上顶点的序号:\n");
scanf("%d,%d",&i,&j);
e=( EdgeNode *)malloc(sizeof(EdegeNode)); //向内存申请空间
//生成边表节点
e->adjvex=j;
e->next=G->adjList[i].firstedge; //将e指针指向
//当前顶点指向的结点
G->adjList[i].firstedge=e; //把当前顶点的指针指向e
e=( EdgeNode *)malloc(sizeof(EdegeNode));//无向图中
//一条边对应两个顶点
e->adjvex=i;
e->next=G->adjList[j].firstedge;
G->adjList[j].firstedge=e;
}
}
一个数据类型后面加*代表创建一个属于这个数据类型的指针
建立边表的过程实际上是应用了单链表创建中的头插法