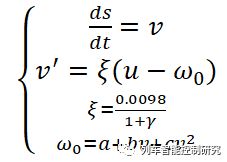基于自抗扰控制的高速列车自动驾驶速度控制
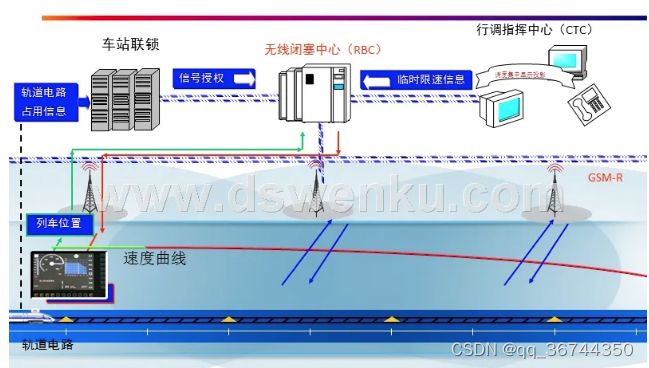
随着高速列车运行速度的快速提高,原有的司机操作加列车防护系统(Automatic train protection ,ATP)监督的运行机制无法保证列车安全快速运行的同时兼顾列车的运行效率,因此,向高速列车添加列车自动驾驶系统(Automatic train operation ,ATO)是当下研究热点。
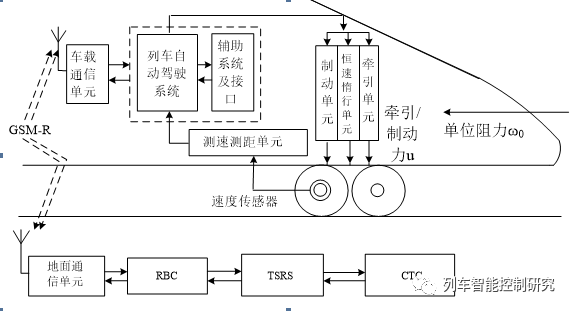
如图1所示,列车共受到单位阻力ω0和牵引/制动力u两个力,视列车整体为一刚性质点,对列车进行力学建模,得到高速列车单质点模型如(1)式。
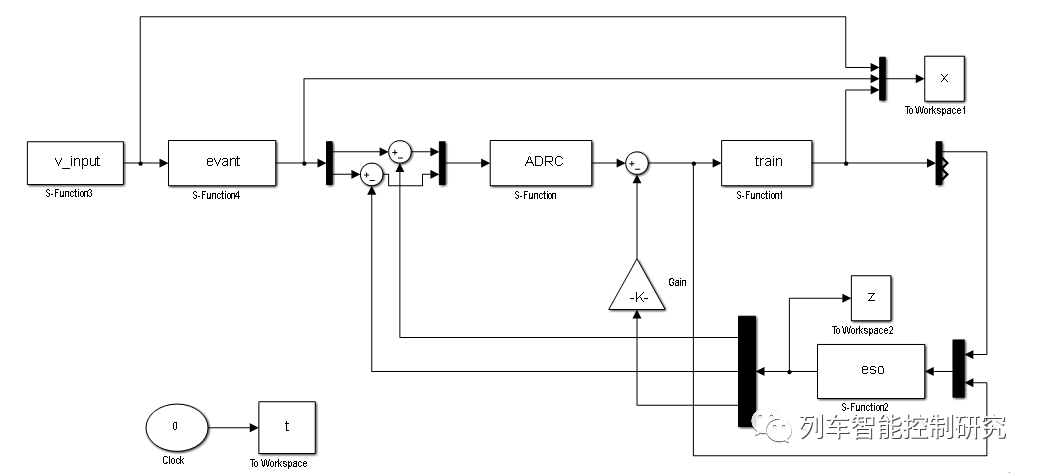
控制器结构图:
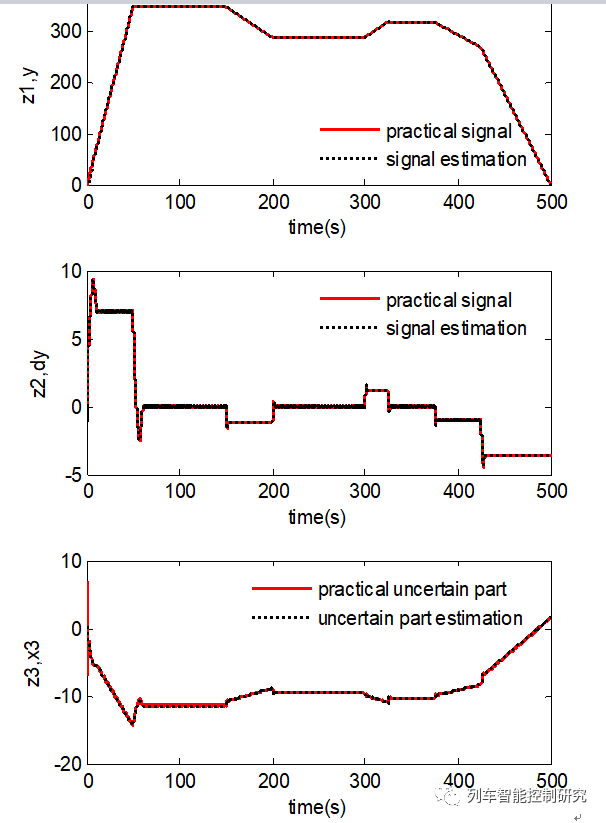
速度追踪结果:
针对高速列车在复杂环境易受未建模动态和外界干扰的问题,设计了基于自抗扰控制的列车速度追踪算法,即保留传统PID反应快、设计简单的优点,又对其强干扰作用下稳定性不高、鲁棒性差的缺点进行了改进,与传统PD控制和非线性PID控制在速度追踪和位移追踪方面做对比可以发现,基于ADRC的列车速度追踪算法具有追踪性能好、停车精度高的优点。
代码示例:
train模块
function [sys,x0,str,ts]=s_function(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case {2, 4, 9 }
sys = [];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 3;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 0;
sys=simsizes(sizes);
x0=[0.15;0];
str=[];
ts=[];
function sys=mdlDerivatives(t,x,u)
ut=u(1);
f=-0.00047*x(2)-0.00001*(x(1).^2)-0.0014; %Uunknown part
b=0.00883;
sys(1)=x(2);
sys(2)=f+b*ut;
function sys=mdlOutputs(t,x,u)
f=-0.00047*x(2)-0.00001*(x(1).^2)-0.0014; %Uunknown part
sys(1)=x(1);
sys(2)=x(2);
sys(3)=f;
evant模块
function [sys,x0,str,ts] = Differentiator(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case {2, 4, 9 }
sys = [];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 2;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [0 0];
str = [];
ts = [0 0];
function sys=mdlDerivatives(t,x,u)
vt=u(1);
e=x(1)-vt;
alfa=1;
nmn=5;
sys(1)=x(2)-nmn*(abs(e))^0.5*sign(e);
sys(2)=-alfa*sign(e);
function sys=mdlOutputs(t,x,u)
sys = x;
evant模块
function [sys,x0,str,ts] = Differentiator(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case {2, 4, 9 }
sys = [];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 2;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [0 0];
str = [];
ts = [0 0];
function sys=mdlDerivatives(t,x,u)
vt=u(1);
e=x(1)-vt;
alfa=1;
nmn=5;
sys(1)=x(2)-nmn*(abs(e))^0.5*sign(e);
sys(2)=-alfa*sign(e);
function sys=mdlOutputs(t,x,u)
sys = x;