基于通用学习环境和多智能体深度强化学习的列车运行图

‍

1. 文章信息

《Train timetabling with the general learning environment and multi-agent deep reinforcement learning》是2022年发表在Transportation Research Part B上的一篇文章。

2. 摘要

针对不同铁路系统的列车运行图问题，本文提出了一种多智能体深度强化学习方法。建立了一个通用的列车运行图学习环境，将该问题建模为一个马尔可夫决策过程，其中问题的目标和复杂约束可以自然而优雅地分散。通过微妙的变化，环境可以在广泛使用的双线铁路系统和更复杂的单线铁路系统之间灵活切换。为了解决多维度的问题，提出了一种多智能体演员评论家(actor-critic)算法框架，将大型组合决策空间分解为多个独立的决策空间，并通过深度神经网络参数化。使用一个真实的实例和几个测试实例对所提出的方法进行了测试。实验结果表明，该方法能在合理的计算时间内得到单线列车运行图问题的协同策略，且在解的最优性方面优于现有几种方法，且只需稍微改变环境即可推广到双线列车运行图问题。

3. 引言

铁路系统以其高运力和高速度成为重要的运输方式。在中国，每年修建大量的高速铁路。2020年，全国铁路总里程达14.6万公里，其中双线铁路占59.3%，其余为单线铁路。对于这两种铁路系统，列车运行图是确定列车发车和到站时间的核心方案。然而，目前的列车运行图工作是由运营人员手工完成的，这就导致了效率低，列车运行图的质量依赖于运营人员的能力等问题。为了减少运营人员的时间和精力，提高对乘客的服务质量，开发一种智能方法来解决列车运行图问题(TTP)具有重要意义。

在本研究中，我们关注的是非周期宏观TTP。非周期是指一天没有被分成多个周期；因此，全天的列车运行图没有明显的规律性。我们考虑铁路系统细节的宏观层面，这意味着基础设施的微观细节被忽略，如车站的轨道数量。更具体地说，我们根据给定的线路规划(即已知要安排的列车数量、运行方向和所有列车的路线)和预先指定的所有列车在始发站的发车时间，确定一条线路上每个车站的列车时刻表。这是在考虑了所有列车的旅行时间最小化的目标和现实世界的约束条件下实现的，包括发车间隔、最小和最大停站时间、加减速时间损失。

在单线铁路系统中，每对列车在反向或同向运行时都有潜在的冲突风险，因为它们争夺轨道运力。然而，预期的结果是为了达到一个共同的目标(快速完成旅程，且没有冲突)而妥协(而不是像围棋那样的零和游戏)，这就导致了列车之间一定程度的合作。我们的初步计算实验表明，传统的单智能体学习方法在这种复杂的竞争-合作场景中表现不佳。在双线铁路系统中，不同方向的列车在两条轨道上运行，显著提高了轨道运力，避免了相反方向列车的冲突风险。因此，双线铁路系统的博弈关系和大部分发车间隔约束都比单线铁路系统要宽松得多。

本文提出了一种新颖而通用的多智能体深度强化学习(MDRL)方法，该方法可应用于单线和双线铁路系统的TTP问题。根据MDRL的设置，一组智能体与环境解耦。每个智能体代表一列待调度的列车，学习如何与其他智能体妥协，以达到从与环境的交互中学习最优合作策略的共同目标。建立了一个通用的列车运行图学习环境，将其系统动力学建模为马尔可夫决策过程(MDP)。我们采用集中训练和分散执行的多智能体演员评论家(MAA2C)算法框架，将其分解为仿真和训练过程。仿真过程模拟智能体与列车运行图学习环境之间的交互，以收集经验。所有智能体都观察他们的局部状态，并根据策略执行动作；然后受到动作影响的列车运行图学习环境就会进入一个新的状态，并向每个智能体反馈一个强化信号(奖励)。所有智能体的经验都存储在共享内存中。集中训练过程利用这些经验训练所有智能体，以改进其策略。训练结束后，所有学习到最优合作策略的智能体将在执行阶段生成最优的列车时刻表。实验结果表明，该方法在单线和双线情况下都能得到最优解；此外，在解决方案的最优性方面，该结果优于几种现有的方法。

贡献

本文的主要贡献如下。

首先，提出了一个通用的学习环境，将TTP建模为一个MDP，可以应用于复杂的单线铁路系统和广泛使用的双线铁路系统。两种铁路系统考虑的目标和约束都优雅地分布在环境模块中。目标表现为奖励函数。在运输动力学中，所有发车间隔约束都可以很容易地检测到，其中加减速时间损失也可以自然地考虑，可选动作集中考虑了最小和最大停站时间约束。注意，在数学规划中，要使所有的约束都易于处理，尤其是加减速的时间损失。除约束检测模块外，其他模块和环境设置都是通用的。因此，环境可以灵活地在不同的系统之间切换。

然后，为了解决混合竞争-合作环境下的维数问题和非平稳性问题，我们提出了一个MAA2C算法，其中每个智能体代表一列列车来决定局部动作。根据A2C架构，每个智能体拥有两个DNN：actor网络进行决策，集中式critic网络从全局角度评估actor网络产生的动作的价值。因此，大的组合决策空间可以分解为多个独立的决策空间，并由DNN参数化。此外，我们采用集中训练和分散执行的算法框架，其中集中的critic网络可以访问其他智能体的决策策略，以促进智能体之间的合作和训练过程的稳定性。

最后，对该方法进行了单线和双线的试验。实验结果表明，该方法在实际单线和双线情况下得到的最优解在解的最优性方面优于几种现有方法。

4. TTLE环境

核心思想

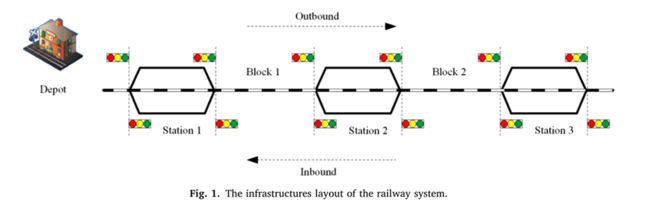
我们考虑由一系列车站I={1,2,...,I}组成的铁路线的一般设置。每个车站i∈I都有几个岔道供火车通过或会合。特别是起始站i=1有一个机务段，从这里发车的列车称为出站列车，返回的列车称为进站列车。车站由一系列区段B={1,2,...,B}连接。基础设施的布局如图1所示。

该模型旨在建立宏观TTP的系统动力学模型，可应用于单线和双线铁路系统。主要用于仿真过程中，通过与智能体交互来生成经验。精度、灵活性和高计算效率是必需的。为了简化系统动力学，我们假设列车以最大速度运行以充分利用轨道运力，列车在区段内的运行时间可以离散为纯运行时间、加速度损失时间和减速损失时间三部分。只要我们知道列车在一个车站是否停车和发车时间，以及列车在下一站停站的时间，我们就可以确定列车在下一站的到达和发车时间。这样就可以忽略列车的加减速过程，认为列车在车站之间是匀速行驶的，这样就可以更简单地确定行驶过程。这使得我们可以将列车在区段中的连续行驶过程离散化，并将TTP视为一个MDP，其中每个时间步指的是铁路沿线上的区段。

然后，我们可以基于上述的核心思想构建TTLE。系统动态如图2所示，它简要地描述了环境状态如何受智能体动作的影响，并从时间步t移动到t+1。在图2(a)和图2(c)中，我们使用简化的列车运行图来表示环境状态。时间从左到右递增。运行图由多个垂直堆叠的矩形组成，其中一个矩形代表一个区段。区段的索引从上到下递增。每个白色填充的矩形表示该列车的运行过程将被安排(由外部周围的虚线框突出显示)或已在此区块内调度，每个灰色填充的矩形表示该列车的运行过程尚未被安排。矩形内的实线表示在区段中出站列车的行进过程(为了简单起见，这里只考虑一列火车)。在时间步t时，我们关注的区段的索引用bt (bt∈B)表示，bt的后站和前站(以出站方向为参考)的索引分别用it和it+1表示。在一条铁路线中，由于每个区段bt连接一对站点(it, it + 1)，因此区段数量总是比站点数量少1 (B = I−1)，且bt的值与it的值相等。在图2(b)中，列车控制智能体在it+1站的停站时间用at表示。有两种情况：列车在下一站it+1停站at分钟(at≠0)，或者直接通过下一站it+1 (at= 0)。给定列车的出发时间以及是否在it站停车，当at已经确定时(这里，我们选择at = 0)，列车在it+1站的到达和出发时间就可以确定。由此也可确定列车在bt区段的运行过程。然后以列车的出发时间和是否停在it+1站作为先验信息(状态)，推导出bt+1区段列车在下一个时间步t+1的运行过程。这样，给定列车在始发站出发的时间，通过智能体在每个时间步的动作，TTLE就可以逐步模拟列车在每个区段的行驶过程。

除了处理系统动态之外，在仿真过程中，TTLE还必须向每个智能体提供一个奖励信号，以评估当前状态下的即时动作有多好，这将被存储在共享内存中，并用于在以后的训练过程中改进其策略。此外，当系统在过渡过程中发生列车冲突时，会中断仿真过程，因此环境必须有回退或复位机制。这涉及到两个重要模块：约束检测和分数分配。在智能体学习到合作策略之前，每对列车之间可能会发生冲突。因此，我们提出了一个约束检测模块，在确定了各列车在当前区段的后站和前站的出发和到达时间后，验证各列车在行驶过程中是否与其他列车发生冲突。如果存在冲突，我们会给智能体分配一个“坏”分数(奖励信号)来惩罚他们导致冲突的行为，然后在下一个时间步中将环境状态重置为初始区段。否则，我们给智能体分配正常的奖励，环境状态在下一个时间步t←t+1时移动到下一个区段bt←bt+1。下面几小节介绍了TTLE的系统动态、约束检测和分数分配模块的制定。TTLE中使用的符号见表1。

系统动态

给定出发站列车的基础设施、线路规划、出发时间，TTLE模拟列车N={1,2,...,N}在所有区段B={1,2,...B}的行驶过程。在时间步t环境由所有列车n∈N的局部状态snt组成的联合状态元组表征。局部状态snt=(xnt,ynt,znt)包含列车n在it站的出发时间xnt，一个二进制变量ynt代表列车n是否在车站it停车，和一个二进制值znt代表列车n的运行方向。如果列车n直接通过车站it，ynt等于0，否则为1。如果列车n是出站列车，znt等于0，如果是进站列车，znt等于1。一旦提供线路规划，所有列车n∈N的为固定值。为了简单起见，我们统一了进站列车和出站列车的符号。以出站方向为参考，进站列车的运行过程实际上与出站列车的运行过程相反。这导致出站列车和进站列车之间的过渡动力学公式不同，这是区分列车运行方向的原因。

根据观察到的状态St, 包含所有列车局部动作ant的一系列动作At={ant|n∈N}由所有控制智能体n∈N决策。动作ant是列车n在区段bt的前站it+1的停站时间。每个动作ant选自一个可选动作整数集U⊂Z，其中包含0(如果列车n直接通过车站it+1)和一个从最小停站时间umin到最大停站时间umax的时间序列。最小停站时间保证了乘客有足够的时间上下车、货物装卸、列车穿越、超车等。设置最大停站时间是为了避免列车在车站停留时间过长，减小动作空间的大小。

然后TTLE根据系统动力学St+1 ~ P(St, At)计算下一个状态St+1。列车n到达it +1站的时间dn t+1需要先确定。

式中wbt为区段bt的自由运行时间，v, u分别为加减速时间损失。Θ(ant)是一个阶跃函数，表示列车n是否在it+1站停车。如果ant=0，Θ(ant) = 0；否则，Θ(ant) =1。出站列车n(znt= 0)从站点it到站点it+1至少需要wbt分钟。如果它在it站停车(ynt=1)，它需要增加额外的启动时间v。如果它在it+1站停车(ant≠0)，额外的制动时间u也必须增加。对于进站列车来说，这个过程是完全相反的。

那么，对于出站列车n，it +1站的发车时间xn t+1为到达时间dn t+1与停站时间ant之和。对于进站列车n, xn t+1等于dn t+1减去ant。

目前，我们可以知道每列列车n∈N在it和it +1站的时间，在it站的出发时间xnt，以及所有列车n∈N在it +1站的到达时间dn t+1和出发时间xn t+1。在计算下一个状态之前，我们检测每列列车是否满足约束(详见2.3节)。如果不存在列车冲突，则TTLE的状态S t+1={sn t+1|n∈N}将过渡到下一个区段bt+1。对于每列列车的局部状态，由式(2)给出，yn t+1等于Θ(ant)，zn t+1等于znt。否则，在下一个时间步，我们将TTLE重置为初始状态，其中xn init为预先设定的起始站出发时间，对于所有列车n∈N，yn init为1，因为列车要在起始站停车，zn init由线路规划确定。

约束检测

为了计算智能体的奖励信号，同时禁止列车冲突，我们在每个时间步t上，根据每列列车n∈N在it和it+1站的已知时间点进行约束检测：xnt，dn t+1和xn t+1。

在单线铁路系统中，连续两列列车在相反方向运行时，必须考虑两个车头时距约束。在图3中，时间从左到右递增。两条平行的水平线代表两个连续的站点，it和it+ 1。站点上的圆对应时间节点(1分钟)。不同方向运行的两列列车n和n'分别用不同颜色(红色和蓝色)的两条线表示，它们在两个站点上的时间点在相应的时间节点内用较小的有颜色的实心圆突出显示。对于列车n和n'，车头时距ψ必须在车站it+1的到达时间之间被满足，而车头时距φ必须在车站it+1的到达时间和出发时间之间被满足，如下所示：

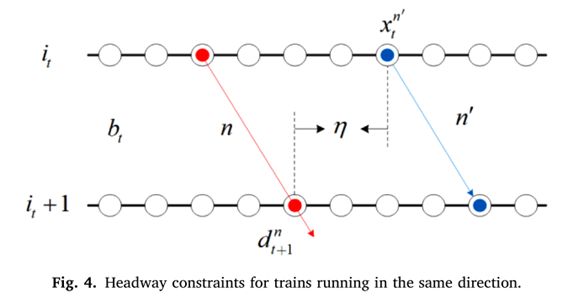
如图4所示，在同一方向连续运行的两列列车n和n'要求进入同一区段bt时，下一列列车n'在it站出发的时间与前一列列车n在it+1站到达的时间之间的车头间距η必须满足下式：

在仿真过程中不考虑列车之间的优先级，采用简单的过线检测方法，禁止交叉和超车冲突。图5(a)中，在区段bt处，运行方向相反的两列列车n与n'发生交叉冲突；图5(b)中，运行方向相同的两列列车n与n'在区段bt发生超车冲突。为了检测交叉和超车冲突，引入pit和pit+1两个参数分别表示it站和it +1站的虚拟空间坐标。两列列车在it和it+1站已知的时间点可以作为时间坐标。然后，我们可以通过简单的数学计算，快速检测出任意一对列车的两条线是否相交。每个区段bt∈B中每列列车n∈N的线由两个节点(xnt,pit)和(dn t+1,pit+1)确定，为了简单起见，其中pit和pit+1分别设为1和0。

在双线铁路系统中，如高速铁路系统和地铁系统，我们只需要考虑同一方向连续两列列车之间的轨道间距。在图6中，当列车n跟随列车n'在区段bt中运行时，两列列车到达it+1站的时间间隔Ψ必须满足下式：

此外，有一个规划范围H，没有列车可以超出它运行，因为在其他时间的维护可能会阻塞轨道线。我们将H定义为时间范围[H, H]，并将其离散为一天的时间单元(例如，分钟)，其中H和H分别为规划范围的下界和上界。那么，禁止列车超出H运行的约束可以表示为

为每列列车引入一个二元变量cn，以记录某列列车是否违反了任何约束。如果列车n违反了任何约束条件，则设置cn=1，否则设置cn=0。在每个时间步，我们为每列列车n∈N重置cn=0。在单线铁路系统中，我们检查每对列车的连接车头时距约束(3)-(5)和交叉/超车冲突约束。在双线铁路系统中，对同一方向的每对列车检查车头时距约束(6)和超车冲突约束。然后，在两个铁路系统中，我们检查所有列车的独立约束(7)，以禁止它们超出规划范围运行。

分数分配

在时间步t的系统转换过程中，TTLE需要给每个智能体分配一个分数(奖励信号)。分数的核心思想是鼓励对目标有贡献而不违反约束的动作，对违反约束而与目标相悖的动作进行惩罚。对于一些多智能体环境，由于仿真过程中获得的奖励过于稀疏，导致分数分配困难，如DOTA II。在本文中，TTLE在每个时间步上模拟了一个区段中每列火车的行驶过程。如前所述，目标是使所有列车的总运行时间最小化，即所有区段列车运行时间之和。因此，在时间步t中，对于每列列车，TTLE中的分数分配是直接的：对于未违反约束条件的列车，奖励为其在区段bt中的运行时间的负数；否则，奖励就是一个负的惩罚。所有智能体的奖励集合表示为Rt+1={rn t+1|n∈N}，其中局部奖励rn t+1可以表示为

为了提高训练过程的有效性，需要从运行时间中扣除一个不变的、不影响决策的wbt。M为正的惩罚因子，大于任意列车在任意区段的运行时间。

5. 多智能体深度强化学习算法

算法框架

我们采用了一个MAA2C算法框架，用于分散式执行的集中训练。每个待调度列车授权的智能体拥有两个DNN：分散式演员网络和集中式评论家网络。演员网络将从TTLE接收到的局部状态映射到局部动作，从而控制相应列车在车站的停站时间。在集中式评论家网络中增加其他智能体状态和行为的额外信息，从全局的角度评估动作价值，是保持智能体之间交互和稳定系统过渡的关键机制。它将所有智能体的状态和动作作为输入，并输出相应智能体的标量值。集中式评论的核心思想是，在环境的系统过渡中，如果每个智能体都知道其他智能体所采取的动作，那么即使策略发生变化，环境也是静止的：

其中S'为S的下一状态，πn和π' n表示智能体 n的不同策略，省略时间步的角标。

算法框架概述如图7所示。在图7(a)中，算法可以分解为仿真和训练两个过程。在仿真过程中(详见3.3节)，智能体与TTLE交互生成经验，并存储在回放缓冲区D中。在训练过程中(详见3.4节)，智能体从D中提取经验来训练他们的演员网络和评论家网络。各智能体之间的交互很简单，每个智能体通过从共享回放缓冲区D中提取的经验来考虑其他智能体的状态和动作的额外信息。图7(b)中，用不同颜色的箭头表示了TTLE、演员网络和评论家网络之间的信息流。如图绿色箭头所示，TTLE将局部状态sn发送给演员网络，然后演员网络做出一个动作并返回到TTLE进行仿真。如黄色和蓝色箭头所示，评论家网络以所有智能体的经验作为输入，输出价值估计，更新自身和演员网络的参数。表2列出了算法中使用的符号。

智能体架构

根据MAA2C架构，每个智能体n拥有两个DNN。演员网络πn将局部状态snt映射到表示U中所有可选动作偏好的logits向量δnt~πn(snt)。体系结构如图8(a)所示。输入层作为输入接收snt。第一和第二隐藏层是全连接的，包含256个神经元，其次是ReLU作为激活函数。输出层是一个全连接的线性层，输出嵌入logits向量δnt。

集中式价值网络qn从全局角度评估列车n的状态-动作对的价值。qn以所有列车n∈N的状态St和动作At连接的元组作为输入。qn的隐藏层与πn的隐藏层相同。输出层全连接到单个神经元以输出标量值估计。结构如图8(b)所示。

仿真过程

在仿真过程中，在每一回合开始时，将TTLE重置为初始状态Sinit。在时间步t时，TTLE向每个智能体n发送局部状态snt，每个智能体根据logits向量δnt~πn(snt)执行一个动作ant。首先，对δnt应用softmax分类器，得到归一化概率ωnt：

然后，利用ε-贪婪方法从概率ωnt中选取ant，其中ε为探索参数。在选择每个动作之前，会根据0和1之间的均匀分布产生一个随机数。如果随机数大于ε，则选择概率最大的动作。否则，从U中随机选择一个动作。为了在仿真的初始阶段进行充分的探索，ε被线性退火为

其中tg表示全局时间步。是终止ε退火的阈值。εmin和εmax分别为ε的下界和上界。

当得到所有智能体的动作后，TTLE按照St+1 ~ P(St, At)进行系统转换操作，并计算所有智能体的奖励Rt={rnt|n∈N}。之后将经验(St, At, Rt+1, St+1)存储在经验回放缓冲区D中。更新时间步t=t+1，继续上述过程。如果所有列车在时间步t+1到达目的站(bt+1=B)，则TTLE到达终止状态ST。保存当前回合的总时间步长T=t+1，重置时间步t=0，启动新的回合ℓ=ℓ+1。

训练过程

DNNs的训练过程可以看作是通过随机梯度下降法解决一个参数优化问题(如本研究中使用的Adam算法)，迭代更新DNNs的参数以最小化损失函数。为了加快和稳定训练过程，采用随机批量优化通过从D中随机抽样的一小批经验K来更新参数。

演员网络的目标是寻找最优合作策略。根据最优策略选择的行动可以从全局的角度最大化任何状态-动作对的未来收益期望，该预期由集中式评论家网络qn估计。给定一小批经验(Sk, Ak, Rk ', Sk ')，k = 1,2，…， K，其中下标k'表示k的下一步，演员网络πn的损失函数L(θn)可以表示为

其中整体状态集Sk被划分为snk和，并且是其他列车的局部状态子集，整体logit集合At也是如此。

集中式评论家网络的目标是最小化价值估计与目标值之间当时的误差。集中式评论家网络qn的损失函数L(μn)可以表示为

其中yk是与抽样经验相关联的目标值，k=1,2,…,K，可以表示为

其中γ是决定当前时间未来价值的折扣因子。为了稳定和加速训练过程，为每个智能体n∈N引入两个目标网络π'n和q'n，以削弱连续状态Sk和Sk'之间的相关性。目标网络π'n和q'n的结构分别与πn和qn相同，其参数θ'n和μ'n通过如下移动平均方法更新：

ξ是一个足够小的平滑因子。

训练过程重复E次，总结在算法1中。

6. 数值实验

本文基于三个案例及其拓展案例，分别在单线和双线情况下进行了数值实验，结果表明，本文提出的方法无论是在复杂的单线铁路系统还是在广泛应用的双线铁路系统中，都可以在不使用任何启发式算法的情况下找到最优解，并且在解的最优性、通用性和鲁棒性方面均优于现有的几种方法。

Attention

欢迎关注微信公众号《当交通遇上机器学习》！如果你和我一样是轨道交通、道路交通、城市规划相关领域的，也可以加微信：Dr_JinleiZhang，备注“进群”，加入交通大数据交流群！希望我们共同进步！