AVL树(平衡二叉树)与红黑树(RBTree)
1. AVL树
一棵AVL树或者是空树,或者是具有下列性质的二叉查找树——它的左子树和右子树都是AVL树,且左子树和右子树的高度之差的绝对值不超过1
2.红黑树
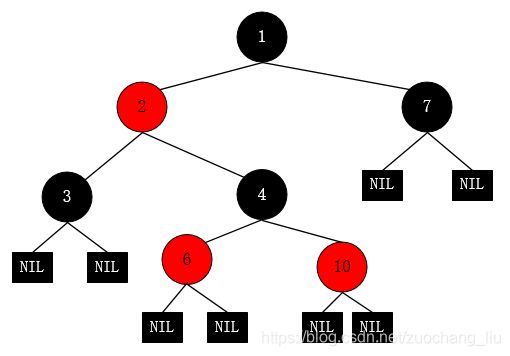
红黑树是一种二叉树,同时它还满足下列5个特性:
- 每个结点是黑色或者红色。
- 根结点是黑色。
- 每个叶子结点(NIL)是黑色。 [注意:这里叶子结点,是指为空(NIL或NULL)的叶子结点!]
- 如果一个结点是红色的,则它的子结点必须是黑色的。
- 每个结点到叶子结点NIL所经过的黑色结点的个数一样的。[确保没有一条路径会比其他路径长出俩倍,所以红黑树是相对接近平衡的二叉树的!]
3. 比较
和红黑树相比,AVL树是严格的平衡二叉树,平衡条件必须满足(所有节点的左右子树高度差不超过1)。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,红黑树确保没有一条路径会比其它路径长出两倍,因此,红黑树是一种弱平衡二叉树(由于是弱平衡,可以看到,在相同的节点情况下,AVL树的高度低于红黑树)。
4.AVL树的旋转
旋转操作用来重新平衡树的某个部分。通过重新安排结点 ,使结点之间的关系始终保持左子结点小于父结点,父结点小于右子结点。使得该树仍然是一颗二叉搜索树。旋转过后,旋转子树中的所有结点的平衡因子都为+1、-1或0。
AVL树的旋转类型有4种, 分别是LL(left-left)旋转、LR(left-right)旋转、RR(right-right)旋转和RL(right-left)旋转。
为方便理解在何时执行哪一种旋转,设x代表刚插入AVL树中的结点,设A为离x最近且平衡因子更改为2的绝对值的祖先。可以归纳为下面4种处理情况:
4.1 LL旋转
如下图所示,当x位于A的左子树的左子树上时,执行LL旋转。
设left为A的左子树,要执行LL旋转,将A的左指针指向left的右子结点,left的右指针指向A,将原来指向A的指针指向left。
旋转过后,将A和left的平衡因子都改为0。所有其他结点的平衡因子没有发生变化。
4.2 LR旋转
当x位于A的左子树的右子树上时,执行LR旋转。
设left是A的左子结点,并设A的子孙结点grandchild为left的右子结点。
要执行LR旋转,将left的右子结点指向grandchild的左子结点,grandchild的左子结点指向left,A的左子结点指向grandchild的右子结点,再将grandchild的右子结点指向A,最后将原来指向A的指针指向grandchild。
执行LR旋转之后,调整结点的平衡因子取决于旋转前grandchild结点的原平衡因子值。
如果grandchild结点的原始平衡因子为+1,就将A的平衡因子设为-1,将left的平衡因子设为0。
如果grandchild结点的原始平衡因子为0,就将A和left的平衡因子都设置为0。
如果grandchild结点的原始平衡因子为-1,就将A的平衡因子设置为0,将left的平衡因子设置为+1。
在所有的情况下,grandchild的新平衡因子都是0。所有其他结点的平衡因子都没有改变。
4.3 RR旋转
当x位于A的左子树的右子树上时,执行RR旋转。
RR旋转与LL旋转是对称的关系。
设A的右子结点为Right。要执行RR旋转,将A的右指针指向right的左子结点,right的左指针指向A,原来指向A的指针修改为指向right。
完成旋转以后,将A和left的平衡因子都修改为0。所有其他结点的平衡因子都没有改变。
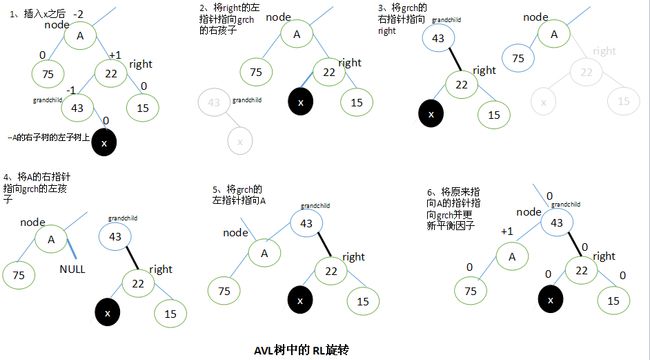
4.4 RL旋转
当x位于A的右子树的左子树上时,执行RL旋转。
RL旋转与LR旋转是对称的关系。
设A的右子结点为right,right的左子结点为grandchild。要执行RL旋转,将right结点的左子结点指向grandchild的右子结点,将grandchild的右子结点指向right,将A的右子结点指向grandchild的左子结点,将grandchild的左子结点指向A,最后将原来指向A的指针指向grandchild。
执行RL旋转以后,调整结点的平衡因子取决于旋转前grandchild结点的原平衡因子。这里也有三种情况需要考虑:
如果grandchild的原始平衡因子值为+1,将A的平衡因子更新为0,right的更新为-1;
如果grandchild的原始平衡因子值为 0,将A和right的平衡因子都更新为0;
如果grandchild的原始平衡因子值为-1,将A的平衡因子更新为+1,right的更新为0;
在所有情况中,都将grandchild的新平衡因子设置为0。所有其他结点的平衡因子不发生改变。