(三十七)论文阅读 | 目标检测之PAA
简介
论文聚焦的是在目标检测中的 A n c h o r {\rm Anchor} Anchor分配问题,我们知道, A n c h o r {\rm Anchor} Anchor的分配策略是一个非常重要的环节,这往往决定了后续的边界框回归等操作,进而影响模型最终的性能。论文基于高斯混合模型,提出将 A n c h o r {\rm Anchor} Anchor的得分视为一种概率。同时, A n c h o r {\rm Anchor} Anchor质量的评价指标由分类得分、定位得分和模型参数共同决定。实验结果为采用新的分配策略后,模型在 C O C O {\rm COCO} COCO数据集上达到 S O T A {\rm SOTA} SOTA。论文原文 源码
0. Abstract
在目标检测中,其中一个核心步骤是确定某 A n c h o r {\rm Anchor} Anchor是属于正样本还是负样本,这往往会决定最终模型的性能。论文提出一种新的 A n c h o r {\rm Anchor} Anchor分配策略,它根据模型的训练状态以概率的形式自适应地为 A n c h o r {\rm Anchor} Anchor分配标签。首先,基于模型本身计算 A n c h o r {\rm Anchor} Anchor的得分,并基于分数得到一个概率分布;其次,基于 A n c h o r {\rm Anchor} Anchor的概率将其划分为正样本和负样本。此外,作者调研了训练和测试之间的差异,引入一个预测交并比的分支作为预测框的衡量标准。提出的新匹配策略仅在 R e t i n a N e t {\rm RetinaNet} RetinaNet中添加单个卷积层,并且不需要在同个位置设置多个 A n c h o r {\rm Anchor} Anchor。
论文贡献:(一)基于高斯混合模型提出基于概率的 A n c h o r {\rm Anchor} Anchor分配策略;(二)基于投票机制的后处理方法;(三)基于新的 A n c h o r {\rm Anchor} Anchor分配策略的模型达到 S O T A {\rm SOTA} SOTA。
1. Introduction
对于 A n c h o r {\rm Anchor} Anchor的分配策略,最常用的是在 F a s t e r {\rm Faster} Faster- R C N N {\rm RCNN} RCNN等中基于交并比的方式。如果先验框同真实框的交并比大于给定的正阈值,则将其视为正样本;如果先验框同真实框的交并比小于给定的负阈值,则将其视为负样本。然后基于真实目标的类别和位置执行回归操作。上述方式虽简单便捷,但同时也存在天生的缺陷。该策略仅考虑了交并比单个因素,而没有关注先验框内的具体内容,如背景噪声会对该分配策略造成较大的影响等。
论文基于前人工作,提出一种新的 A n c h o r {\rm Anchor} Anchor分配策略。为了使得最终的分配过程高效,正负样本的数量不应仅基于交并比这一个标准,还要根据模型此时的推理结果。所以,模型应该参与 A n c h o r {\rm Anchor} Anchor分配这一过程,即正负样本的分配依赖于模型本身。如当没有 A n c h o r {\rm Anchor} Anchor与真实框有较高的交并比时,应适当挑选一些 A n c h o r {\rm Anchor} Anchor作为正样本。在该情况下,模型找到一组高质量的 A n c h o r {\rm Anchor} Anchor作为正样本。另一方面,所有高质量的 A n c h o r {\rm Anchor} Anchor都应该作为正样本参与训练。其中最重要的一点是,高质量 A n c h o r {\rm Anchor} Anchor的选取应该基于模型当前的状态。
论文提出一种基于概率的 A n c h o r {\rm Anchor} Anchor分配的策略, P A A {\rm PAA} PAA,它以自适应的方式生成一组正负样本。首先,基于分类和回归的结果为每个 A n c h o r {\rm Anchor} Anchor定义分数,该分数通过损失函数值得到;然后基于模型的状态定义每个 A n c h o r {\rm Anchor} Anchor的最终得分。基于这些得分,找到一个概率分布用于表征正负样本。然后,基于概率分布,将概率更高的 A n c h o r {\rm Anchor} Anchor视为正样本。这就将 A n c h o r {\rm Anchor} Anchor的分配问题转化成概率分布的极大似然估计问题。最后,由于正样本是通过 A n c h o r {\rm Anchor} Anchor的得分分布确定,所以不需要事先预定义正负样本的数量。
经调研,作者发现当前目标检测模型存在训练(最小化分类和回归损失)与测试(仅依赖于分类得分的非极大值抑制)不一致的情况。理想情况下,检测框的质量应该由分类和回归共同决定。由此,论文提出将交并比乘以分类得分作为衡量检测框质量的最终标准。
2. Related Work
Anchor Assignment in Object Detection M e t a A n c h o r {\rm MetaAnchor} MetaAnchor定义一个基于 A n c h o r {\rm Anchor} Anchor的函数,其输入是 A n c h o r {\rm Anchor} Anchor的宽和高,这使得在训练和测试过程中可以动态地改变 A n c h o r {\rm Anchor} Anchor的形状; G u i d e d A n c h o r i n g {\rm GuidedAnchoring} GuidedAnchoring将真实框中心周围的 A n c h o r {\rm Anchor} Anchor作为正样本; F r e e A n c h o r {\rm FreeAnchor} FreeAnchor将准确率和召回率共同作为决定 A n c h o r {\rm Anchor} Anchor正负性的依据; A T S S {\rm ATSS} ATSS基于 A n c h o r {\rm Anchor} Anchor的交并比的均值和方差,自适应地确定 A n c h o r {\rm Anchor} Anchor的正负性。
M A L {\rm MAL} MAL和 N o i s y A n c h o r {\rm NoisyAnchor} NoisyAnchor使用分类和回归结果共同决定 A n c h o r {\rm Anchor} Anchor的正负性。但这类方法也是选择固定数量的最佳 A n c h o r {\rm Anchor} Anchor作为正样本,而没有基于概率动态地选择正负样本。 M A L {\rm MAL} MAL在训练过程中线性地减少正样本的数量; N o i s y A n c h o r {\rm NoisyAnchor} NoisyAnchor在训练过程中固定 A n c h o r {\rm Anchor} Anchor的数量,但也没有直接地将 A n c h o r {\rm Anchor} Anchor的选择与非极大值抑制等后处理操作联系起来。
Predicting Localization Quality in Object Detection Y O L O {\rm YOLO} YOLO和 Y O L O v 2 {\rm YOLOv2} YOLOv2将交并比和分类得分的乘积作为边界框的最终得分; I o U N e t {\rm IoU\ Net} IoU Net提出使用基于交并比的 N M S {\rm NMS} NMS。
3. Proposed Methods
3.1 Probabilistic Anchor Assignment Algorithm
论文的想法是将三个关键的因素考虑进 A n c h o r {\rm Anchor} Anchor的采样中:首先,使用模型来衡量 A n c h o r {\rm Anchor} Anchor的质量;其次,自适应的方式将 A n c h o r {\rm Anchor} Anchor划分正负性;最后,分配策略基于概率最大化。
具体地,将 A n c h o r {\rm Anchor} Anchor的分数定义为能够反应预测框的质量,直观的做法是将分类分数和回归得分相乘,即: S ( f θ ( a , x ) , g ) = S c l s ( f θ ( a , x ) , g ) × S l o c ( f θ ( a , x ) , g ) λ (1) S(f_{\theta}(a,x),g)=S_{cls}(f_{\theta}(a,x),g)×S_{loc}(f_{\theta}(a,x),g)^{\lambda}\tag{1} S(fθ(a,x),g)=Scls(fθ(a,x),g)×Sloc(fθ(a,x),g)λ(1)
S c l s S_{cls} Scls和 S l o c S_{loc} Sloc分别表示分类和回归得分, λ \lambda λ用于控制两个乘积项的权重, x x x和 f θ f_{\theta} fθ分别表示输入图像和带参数 θ \theta θ的模型。则我们可以使用分类头的输出定义 S c l s S_{cls} Scls的值,使用交并比定义 S l o c S_{loc} Sloc的值: S l o c ( f θ ( a , x ) , g ) = I o U ( f θ ( a , x ) , g ) (2) S_{loc}(f_{\theta}(a,x),g)={\rm IoU}(f_{\theta}(a,x),g)\tag{2} Sloc(fθ(a,x),g)=IoU(fθ(a,x),g)(2)
对式(1)添加负对数,得到: − log S ( f θ ( a , x ) , g ) = − log S c l s ( f θ ( a , x ) , g ) − λ log S l o c ( f θ ( a , x ) , g ) = L c l s ( f θ ( a , x ) , g ) + λ L I o U ( f θ ( a , x ) , g ) (3) \begin{aligned} -\log S(f_{\theta}(a,x),g)&=-\log S_{cls}(f_{\theta}(a,x),g)-\lambda \log S_{loc}(f_{\theta}(a,x),g) \\ &=\mathcal L_{cls}(f_{\theta}(a,x),g)+\lambda \mathcal L_{IoU}(f_{\theta}(a,x),g) \end{aligned}\tag{3} −logS(fθ(a,x),g)=−logScls(fθ(a,x),g)−λlogSloc(fθ(a,x),g)=Lcls(fθ(a,x),g)+λLIoU(fθ(a,x),g)(3)
为了使得模型能够以概率的方式来判断某个 A n c h o r {\rm Anchor} Anchor是否属于正样本,做法是对于某个真实框对 A n c h o r {\rm Anchor} Anchor的分数建模,然后基于概率将 A n c h o r {\rm Anchor} Anchor划分为正负。由于目的是将一组 A n c h o r {\rm Anchor} Anchor划分为正样本和负样本,论文使用高斯混合模型: P ( a ∣ x , g , θ ) = w 1 N 1 ( a ; m 1 , p 1 ) + w 2 N 2 ( a ; m 2 , p 2 ) (4) P(a|x,g,\theta)=w_1\mathcal N_1(a;m_1,p_1)+w_2\mathcal N_2(a;m_2,p_2)\tag{4} P(a∣x,g,θ)=w1N1(a;m1,p1)+w2N2(a;m2,p2)(4)
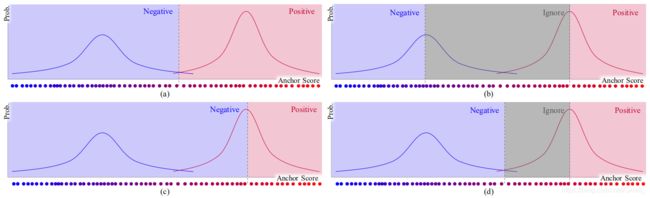
w w w、 m m m和 p p p分别表示权重、均值和准确率,给定一组 A n c h o r {\rm Anchor} Anchor的分数,使用 E M {\rm EM} EM算法可以优化该 G M M {\rm GMM} GMM。使用 E M {\rm EM} EM优化得到的 G M M {\rm GMM} GMM,我们可以根据 A n c h o r {\rm Anchor} Anchor概率将其划分成正样本或负样本。下图是几种典型的划分方式:
算法输入是真实框 G {\mathcal G} G、 A {\mathcal A} A、第 i i i层的 A i {\mathcal A_i} Ai、金字塔层数 L {\mathcal L} L和金字塔每层的 A n c h o r {\rm Anchor} Anchor数 K {\mathcal K} K,输出是正负样本集合 P {\mathcal P} P、负样本集合 N {\mathcal N} N和忽略样本集合 I {\mathcal I} I。第三行,初始状态使用与真实框有最高交并比的 A n c h o r {\rm Anchor} Anchor;第六行,确定金字塔每一层的 A n c h o r {\rm Anchor} Anchor为 A i g {\mathcal A_i^g} Aig;第七行,基于公式(3)计算 A n c h o r {\rm Anchor} Anchor的得分 S i {\mathcal S_i} Si;第八行,找到第 K {\mathcal K} K个最高得分的 A n c h o r {\rm Anchor} Anchor为 t i t_i ti;第九行,获得前 K {\mathcal K} K个最高得分的 A n c h o r {\rm Anchor} Anchor为 C g i {\mathcal C_g^i} Cgi;第十二行,使用 E M {\rm EM} EM优化 G M M {\rm GMM} GMM;第十三行,划分正负样本。
为了概率算法整体以及将其应用到检测器中,损失函数定义如下: arg max θ ∏ g ∏ a ∈ A g P p o s ( a , θ , g ) S p o s ( a , θ , g ) + P n e g ( a , θ , g ) S n e g ( a , θ ) (5) \argmax_{\theta}\prod_g\prod_{a\in \mathcal A_g}P_{pos}(a,\theta,g)S_{pos}(a,\theta,g)+P_{neg}(a,\theta,g)S_{neg}(a,\theta)\tag{5} θargmaxg∏a∈Ag∏Ppos(a,θ,g)Spos(a,θ,g)+Pneg(a,θ,g)Sneg(a,θ)(5)
S p o s ( a , θ , g ) = S ( f θ ( a ) , g ) = exp ( − L c l s ( f θ ( a ) , g ) − λ L I o U ( f θ ( a ) , g ) ) (6) \begin{aligned} S_{pos}(a,\theta,g)&=S(f_{\theta}(a),g) \\ &=\exp(-\mathcal L_{cls}(f_{\theta}(a),g)-\lambda \mathcal L_{IoU}(f_{\theta}(a),g)) \end{aligned}\tag{6} Spos(a,θ,g)=S(fθ(a),g)=exp(−Lcls(fθ(a),g)−λLIoU(fθ(a),g))(6)
S n e g = exp ( − L c l s ( f θ ( a ) , ∅ ) ) (7) S_{neg}=\exp(-\mathcal L_{cls}(f_{\theta}(a),\varnothing))\tag{7} Sneg=exp(−Lcls(fθ(a),∅))(7)
3.2 IoU Prediction as Localization Quality
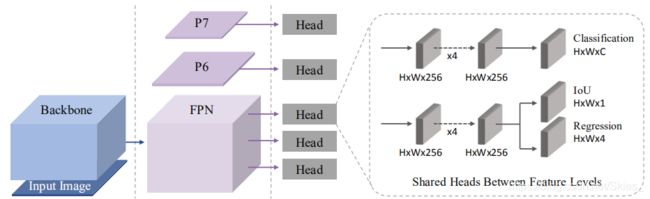
由于在训练和测试过程中均需要使用交并比来衡量预测框的质量,论文提出将模型扩展为直接预测边界框与之对应真实框的交并比,通过添加一个卷积层针对每个 A n c h o r {\rm Anchor} Anchor输出一个标量值。则最终的损失函数还需要加上这一分支的结果: L ( f θ ( a ) , g ) = L c l s ( f θ ( a ) , g ) + λ 1 L I o U ( f θ ( a ) , g ) + λ 2 L I o U P ( f θ ( a ) , g ) (8) \mathcal L(f_{\theta}(a),g)=\mathcal L_{cls}(f_{\theta}(a),g)+\lambda_1\mathcal L_{IoU}(f_{\theta}(a),g)+\lambda_2\mathcal L_{IoUP}(f_{\theta}(a),g)\tag{8} L(fθ(a),g)=Lcls(fθ(a),g)+λ1LIoU(fθ(a),g)+λ2LIoUP(fθ(a),g)(8)
在推理过程中,直接将预测的交并比作为最后非极大值抑制的阈值。
3.3 Score Voting
此外,论文还提出一种简单高效的后处理手段,对于每个预测框 b b b,该方法作用于非极大值抑制后: p i = e − ( 1 − I o U ( b , b i ) ) 2 / σ t (9) p_i=e^{-(1-{\rm IoU}(b,b_i))^2/\sigma_t}\tag{9} pi=e−(1−IoU(b,bi))2/σt(9)
b ^ = ∑ i p i s i b i ∑ i p i s i s u b j e c t t o I o U ( b , b i ) > 0 (10) \hat b=\frac{\sum_ip_is_ib_i}{\sum_ip_is_i}\ {\rm subject\ to\ IoU}(b,b_i)>0\tag{10} b^=∑ipisi∑ipisibi subject to IoU(b,bi)>0(10)
b ^ \hat b b^、 s i s_i si和 σ t \sigma_t σt分别表示更新后的框、式(1)计算的得分和超参数,该算法的主要思想是根据学习到的相邻框之间的方差来选出最佳候选框的位置。该投票方法来自这篇文章,不了解具体内容。
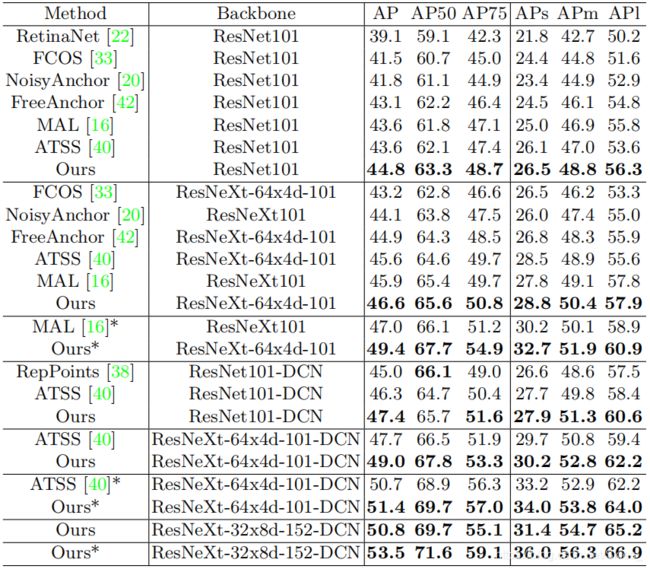
4. Experiments
5. Conclusion
论文提出一种基于概率的 A n c h o r {\rm Anchor} Anchor分配策略,将 A n c h o r {\rm Anchor} Anchor分配过程转化成概率分布的最大化。这样,某个 A n c h o r {\rm Anchor} Anchor的质量由分类得分、定位得分和模型参数共同决定。同时,文中还改进了一种基于投票机制的后处理方法,提高了模型的后处理能力。
参考
- Kim K, Lee H S. Probabilistic Anchor Assignment with IoU Prediction for Object Detection[J]. arXiv preprint arXiv:2007.08103, 2020.