Prophet算法框架趋势模型、季节模型原理详解与应用实践

本文是在ChatGPT协助下完成，提高了写作速度和效率。

1. 趋势模型

1.1. 趋势模型概述

当我们谈论Prophet中的趋势模型时，我们可以将其理解为描述时间序列数据中整体趋势的一种方式。趋势模型可以告诉我们数据随着时间的推移是如何变化的，是增长、减少还是保持稳定。

在Prophet中，有两种常见的趋势模型形式：

• 线性趋势模型：线性趋势模型假设数据的增长或减少是以恒定的速率发生的，即数据以直线的形式随着时间线性变化。这种模型适用于那些呈现出持续性增长或减少趋势的数据。例如，一个产品的销售量随着时间的增加而线性增长。

• 逻辑回归增长模型：逻辑回归增长模型假设数据的增长或减少是以一种饱和的方式发生的，即在某个时间点之后，数据的增长速度逐渐减慢并趋于稳定。这种模型适用于那些呈现出饱和增长趋势的数据，比如人口增长或市场渗透率。逻辑回归增长模型使用S形曲线来描述数据的增长过程，起初增长较快，但随着时间的推移增长速度逐渐减慢。

通过选择合适的趋势模型形式，Prophet能够更准确地捕捉数据中的趋势变化，并提供可靠的预测结果。根据数据的特点和背后的实际情况，我们可以选择线性趋势模型或逻辑回归增长模型来建模数据的整体趋势。这样，我们就可以更好地理解和预测数据随着时间的变化趋势。

在Prophet实际应用中，非线性趋势模型包括两种形式：饱和增长模型（Saturation Growth Model）和分段的逻辑回归增长模型（Piecewise Logistic Growth Model）。

• 饱和增长模型：饱和增长模型假设趋势具有饱和性，即随着时间的推移，趋势会逐渐减缓并趋于稳定。这种模型通常用于描述一些自然增长过程，例如人口增长、产品市场的渗透率等。饱和增长模型可以通过使用S形曲线（通常是Logistic函数）来建模趋势。

• 分段的逻辑回归增长模型：分段的逻辑回归增长模型假设趋势在不同的时间段内具有不同的增长率。它将趋势分为多个片段，并对每个片段应用逻辑回归模型来建模。这种模型适用于一些具有突变或阶段性变化的趋势，例如市场营销活动的影响、政策变化等。

1.2. 趋势模型原理

1.2.1. 非线性趋势模型原理

逻辑回归增长模型采用了Logistic函数来描述数据的增长过程。Logistic函数通常被称为Sigmoid函数，其数学表达式如下：

$g(t)=\frac{C}{1+exp(-k(t-m))}$

其中，$g(t)$表示在时间$t$处的增长趋势的预测值，$C$表示趋势的上限值，$k$表示增长的速率参数，$m$表示趋势的中点位置参数。

但是在现实环境中，函数$C,k,m$ 的三个参数不可能都是常数，而很有可能是随着时间的迁移而变化的，因此，在 Prophet 里面，作者考虑把这三个参数全部换成了随着时间而变化的函数，也就是$C(t),k(t),m(t)$ 。除此之外，在现实的时间序列中，曲线的走势肯定不会一直保持不变，在某些特定的时候或者有着某种潜在的周期曲线会发生变化，这种时候，就有学者会去研究变点检测，也就是所谓 change point detection。

可以假设有这样一个向量： $\delta \in {\mathbb{R}}^{\mathbf{s}}$， 其中： ${\gamma }_j$ 表示在时间戳 $s_j$ 上的增长率的变化量。如果一开始的增长率我们使用 $k$ 来代替的话，在时间$t$上的增长率就是 $k+{\sum }_{j:t>s_j}{\delta }_j$。

${\gamma }_j=(s_j-m-{\sum }_{l<j}{\gamma }_l)(1-\frac{k+{\sum }_{l<j}{\gamma }_l}{k+{\sum }_{l\le j}{\gamma }_l})$

分段的逻辑回归增长模型就是：

$g(t)=\frac{C(t)}{1+exp(-(k+a(t{)}^T\delta )(t-(m+a(t{)}^T\gamma )))}$

在使用 Prophet 的 growth = ‘logistic’ 的时候，需要提前设置好 $C(t)$。

1.2.2. 基于分段线性函数的模型形如：

在分段线性函数模型中，数据的趋势被分为多个时间段，每个时间段都有一个对应的线性函数来描述数据的变化。这种模型的好处是能够更灵活地捕捉数据的变化趋势，适应不同时间段的变化速度。

$g(t)=(k+a(t{)}^T\delta )t+(m+a(t{)}^T\gamma )$

其中 ，$k$ 表示增长率（growth rate）， $\delta$ 表示增长率的变化量， $m$ 表示趋势的中点位置参数 offset parameter。

${\gamma }_j=-s_j{\delta }_j$ 注意：这与之前逻辑回归函数中的设置是不一样的。

分割点，如何计算呢？

• 分析师根据经验去定义。
• 按月按年等，等分
• 随机选取分割间隔，分割间隔服从拉普拉斯分布${\delta }_j\sim Laplace(0,\tau )$。

1.3. 趋势模型应用方法

1.3.1. 基本方法

Prophet的趋势模型形式是由growth参数的设置决定的。当growth设置为linear时，趋势模型形式是线性的，即趋势以线性方式增长或减少。当growth设置为logistic时，趋势模型形式是逻辑回归增长模型，即采用S形曲线来建模趋势的变化。

在Prophet中，趋势模型的形式可以通过设置模型定义时的growth参数来指定。

• linear：表示采用线性趋势模型。这意味着趋势被建模为一个线性函数，即在时间上以恒定的速率增长或减少。

• logistic：表示采用逻辑回归增长模型。这意味着趋势被建模为一个S形曲线，具有饱和增长的特点。

在实际操作中，你可以根据你的数据特点和预测需求来选择适当的趋势模型形式。如果你的数据显示出明显的饱和增长特征或突变点，可以考虑使用逻辑回归增长模型（growth=‘logistic’）。如果你的数据呈现出线性增长或减少的趋势，可以使用线性趋势模型（growth=‘linear’）。

例如，下面是定义Prophet模型时设置趋势模型形式的示例：

from prophet import Prophet

# 定义线性趋势模型
model_linear = Prophet(growth='linear')

# 定义逻辑回归增长模型
model_logistic = Prophet(growth='logistic')

在上述示例中，model_linear使用线性趋势模型，而model_logistic使用逻辑回归增长模型来建模趋势。你可以根据实际情况选择合适的趋势模型形式，以获得更准确的预测结果。

1.3.2. 分段线性模型

在程序里面有两种方法，

• 一种是通过人工指定的方式指定变点的位置；
• 另外一种是通过算法来自动选择。

在默认的函数里面，Prophet 会选择 n_changepoints = 25 个变点，然后设置变点的范围是前 80%（changepoint_range），也就是在时间序列的前 80% 的区间内会设置变点。通过 forecaster.py 里面的 set_changepoints 函数可以知道，首先要看一些边界条件是否合理，例如时间序列的点数是否少于 n_changepoints 等内容；其次如果边界条件符合，那变点的位置就是均匀分布的，这一点可以通过 np.linspace 这个函数看出来。

参数	描述
growth	是指模型的趋势函数，目前取值有2种，linear和logistic
changepoints	是指一个特殊的日期，在这个日期，模型的趋势将发生改变。而changepoints是指潜在changepoint的所有日期，如果不指明则模型将自动识别。
n_changepoints	最大的Changepoint的数量。如果changepoints不为None，则本参数不生效。
changepoint_range	是指changepoint在历史数据中出现的时间范围，与n_changeponits配合使用，changepoint_range决定了changepoint能出现在离当前时间最近的时间点，changepont_range越大，changepoint可以出现的距离现在越近。当指定changepoints时，本参数不生效
changepoint_prior_scale	设定自动突变点选择的灵活性，值越大越容易出现changepoint

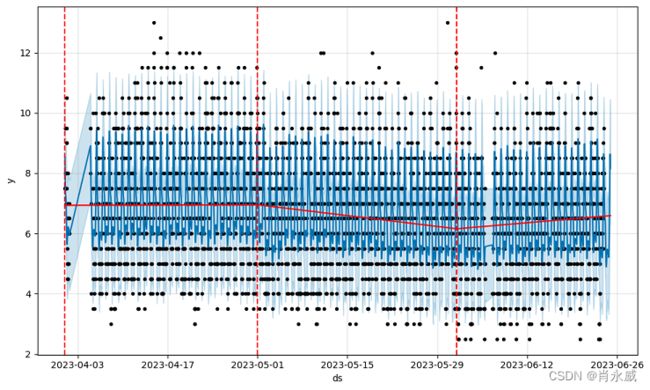
1.3.3. （人工）按月分割案例

changepoints=['2023-04-01', '2023-05-01', '2023-06-01']
model = Prophet(growth='linear',changepoint_prior_scale=5,yearly_seasonality=False, holidays=holidays, changepoints=changepoints)

model.fit(train)
future = model.make_future_dataframe( periods=48, freq='30min', include_history=True)  # 1天
forecast = model.predict(future)

fig = model.plot(forecast)
a = add_changepoints_to_plot(fig.gca(), model, forecast)

# 找到突变时间线
threshold = 0.01
signif_changepoints = model.changepoints[
    np.abs(np.nanmean(model.params['delta'], axis=0)) >= threshold
] if len(model.changepoints) > 0 else []
signif_changepoints

突变时间线。

绘制组件图。

fig = model.plot_components(forecast)

趋势图如上图trend所示，4月用电平稳，5月天气转暖用电降低，6月份天气变热，用电量增加。

2. 季节项模型

2.1. 季节项模型原理

在Prophet中，为了捕捉时间序列数据中的周期性变化，作者引入了季节性组件，该组件使用了傅立叶级数的思想。通过将周期性变化表示为多个正弦和余弦函数的线性组合，Prophet能够更好地建模和预测数据中的周期性模式。

具体而言，Prophet使用了一组傅立叶级数来表示时间序列数据的季节性。每个傅立叶项包含一个正弦和一个余弦函数，并且具有自己的振幅（amplitude）和相位（phase）参数。通过对这些傅立叶项进行线性组合，可以得到整体的周期性季节性组件。

这种傅立叶级数的建模方法使Prophet能够灵活地适应不同时间序列的周期性模式，并且可以自动检测和捕捉数据中的主要周期性特征。通过将周期性建模与趋势建模相结合，Prophet提供了一种综合的时间序列预测框架。

$s(t)={\sum }_{n=1}^N(a_{n}cos(\frac{2\pi nt}{P})+b_{n}sin(\frac{2\pi nt}{P})$

$P=365.25$表示以年为周期或$P=7$表示以周为周期。简而言之，通过截断傅立叶级数，可以控制季节性的频率范围，从而调整对快速变化的季节性模式的拟合能力。对于年度和每周季节性，作者建议将截断参数设置为$N=10$和$N=3$，这些值是通过实验发现在大多数问题中表现良好的。对于参数的选择，可以使用AIC等模型选择过程来自动化。

例如每年季节项的$N=10$，$X(t)=[cos(\frac{2\pi (1)t}{365.25}),...,sin(\frac{2\pi (10)t}{365.25})]$。

因此，时间序列的季节项就是： $s(t)=X(t)\beta$，而$\beta$ 的初始化是 $\beta \sim Normal(0,{\sigma }^2)$。这里的$\sigma$ 是通过 seasonality_prior_scale 来控制的，也就是说 $\sigma =seasonality\_prior\_scale$ 。这个值越大，表示季节的效应越明显；这个值越小，表示季节的效应越不明显。同时，在代码里面，seasonality_mode 也对应着两种模式，分别是加法和乘法，默认是加法的形式。在开源代码中， $X(t)$ 函数是通过 fourier_series 来构建的。

2.2. Prophet 的默认参数

def __init__(
    self,
    growth='linear',
    changepoints=None,
    n_changepoints=25, 
    changepoint_range=0.8,
    yearly_seasonality='auto',
    weekly_seasonality='auto',
    daily_seasonality='auto',
    holidays=None,
    seasonality_mode='additive',
    seasonality_prior_scale=10.0,
    holidays_prior_scale=10.0,
    changepoint_prior_scale=0.05,
    mcmc_samples=0,
    interval_width=0.80,
    uncertainty_samples=1000,
):

解释如下：

• growth: 该参数控制趋势的类型。可选值有linear和logistic，默认值为linear。如果数据的趋势是线性的，则使用linear；如果数据的趋势是S型的，则使用logistic。
• changepoints: 该参数指定趋势变化点的位置。可以传入一个日期列表，或者使用Prophet内置的一些变化点检测算法，如’auto’、‘linear’、'logistic’等。
• n_changepoints: 该参数指定趋势变化点的数量。默认值为25，可以根据数据的特征进行调整。
• changepoint_range: 该参数指定趋势变化点的位置范围。默认值为0.8，表示趋势变化点的位置范围为数据的后80%。可以设置为其他值，如0.5。
• changepoint_prior_scale: 该参数控制模型的灵活性，它决定了模型能够适应数据的程度。较小的值将使模型更加平滑，较大的值将使模型更加敏感。默认值为0.05。
• yearly_seasonality: 该参数控制是否包括年季节性成分。默认值为True。
• weekly_seasonality: 该参数控制是否包括周季节性成分。默认值为True。
• daily_seasonality: 该参数控制是否包括日季节性成分。默认值为False。
• holidays: 该参数指定假期日期。可以传入一个包含假期日期的DataFrame，或者使用Prophet内置的一些假期，如美国的节假日、感恩节、圣诞节等。
• seasonality_mode: 该参数控制季节性成分的计算方式。可选值有additive和multiplicative，默认值为additive。如果数据的季节性随时间变化的幅度不变，使用additive；如果季节性随时间变化的幅度不断增加或减小，则使用multiplicative。
• seasonality_prior_scale: 该参数控制季节性成分的灵活性，它决定了季节性成分对预测的影响。较小的值将使季节性成分影响减小，较大的值将使季节性成分影响增加。默认值为10.0。
• holidays_prior_scale: 该参数控制假期成分的灵活性，它决定了假期对预测的影响。较小的值将使假期成分影响减小，较大的值将使假期成分影响增加。默认值为10.0。
• interval_width: 该参数控制置信区间的宽度。默认值为0.8，表示置信区间为80%。可以设置为0.95或其他值。
• seasonality_prior_scale: 该参数控制季节性成分的灵活性，它决定了季节性成分对预测的影响。较小的值将使季节性成分影响减小，较大的值将使季节性成分影响增加。默认值为10.0。
• seasonality_prior_scale_seasonality: 该参数控制季节性成分的先验分布。可以传入一个字典，指定每个季节性成分的先验分布。例如，{‘weekly’: 5, ‘yearly’: 10}表示周季节性成分的先验分布为5，年季节性成分的先验分布为10。
• seasonality_prior_scale_holidays: 该参数控制假期成分的先验分布。可以传入一个字典，指定每个假期成分的先验分布。
• holidays_prior_scale: 该参数控制假期成分的灵活性，它决定了假期对预测的影响。较小的值将使假期成分影响减小，较大的值将使假期成分影响增加。默认值为10.0。
• growth_prior_scale: 该参数控制趋势成分的先验分布。较小的值将使趋势成分影响减小，较大的值将使趋势成分影响增加。默认值为0.05。

2.3. 自定义季节周期

当使用Prophet进行时间序列预测时，可以通过添加自定义周期来捕捉特定的周期性模式。下面是一个自定义周期为10天的案例：

# 初始化数据，略。
# 创建Prophet模型
model = Prophet()
model.add_seasonality(name='custom_seasonality', period=10, fourier_order=5)

# 拟合数据
model.fit(train)

# 创建未来日期
future_dates = model.make_future_dataframe(periods=48)

# 预测
forecast = model.predict(future_dates)

# 绘制预测结果
model.plot(forecast)

在上面的例子中，我们使用实际项目中的某个时间序列数据。然后，我们创建了一个Prophet模型并添加了一个自定义周期为10天的季节性组件，其中period参数指定了周期的长度，这里设置为10，fourier_order参数指定了傅立叶级数的阶数，这里设置为5。

接下来，我们使用拟合数据进行模型训练，并使用make_future_dataframe方法创建了未来30天的日期。最后，通过调用predict方法获取预测结果，并使用plot方法绘制预测结果的图形。

这样，我们就可以在预测中使用自定义的周期，并对数据中的10天周期性进行建模和预测。

季节项如下图所示：

新增10天的周期性季节项图如下所示：

请注意，根据您的实际数据和需求，您可以根据需要自定义不同的周期长度和傅立叶级数的阶数。

3. 附注

3.1. 拉普拉斯分布

具有密度函数：$f(x)=\frac{1}{2\gamma }{e}^{-\frac{|x-\mu |}{\gamma }}$的分布叫做拉普拉斯分布。

其中，$\mu$ 称为位置参数，$\gamma$称为尺度参数。拉普拉斯分布的期望为$\mu$，方差为$2{\gamma }^2$。

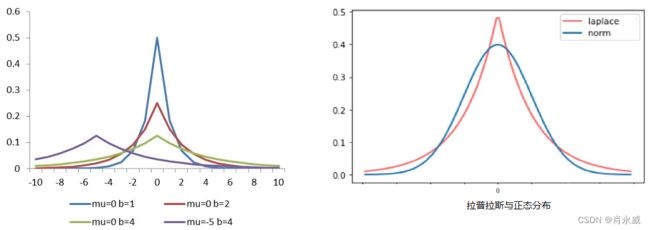
拉普拉斯分布的概率密度与正态分布看起来很像，画出标准拉普拉斯分布（ $\gamma =1$ ）和标准正态分布的概率密度图：

3.2. AIC

赤池信息量准则，即Akaike information criterion、简称AIC，是衡量统计模型拟合优良性的一种标准，是由日本统计学家赤池弘次创立和发展的。赤池信息量准则建立在熵的概念基础上，可以权衡所估计模型的复杂度和此模型拟合数据的优良性。

在一般的情况下，AIC可以表示为：

$AIC=\frac{2k-2L}{n}$

它的假设条件是模型的误差服从独立正态分布。其中：$k$是所拟合模型中参数的数量，$L$是对数似然值，$n$是观测值数目。

参考：

数学人生. Facebook 时间序列预测算法 Prophet 的研究. 知乎. 2018.12

模型视角. 时间序列预测Prophet模型及Python实现. 知乎. 2023.03

肖永威. Prophet 时间序列预测框架入门实践笔记. CSDN博客. 2023.06