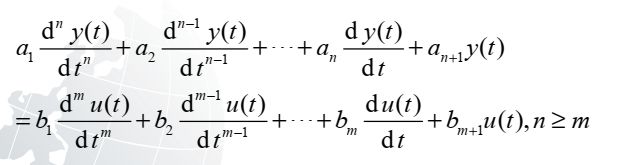MATLAB—信号与系统中的应用

用MATLAB处理信号与系统中的问题，更加直观、方便、准确。

一. 理论知识

1.线性系统的响应

许多实际系统都可以用线性系统来模拟，如果线性系统的参数是常数，则该线性系统可以用线性常系数微分方程来描述，所以，求解线性系统的响应就转换成求线性常系数微分方程的解了！

线性系统响应对应微分方程解
对于一个线性系统，存在激励u(t)和响应y(t)，激励和响应之间的关系可以用微分方程的形式来描述：

其中，a、b为常系数；方程为n阶线性时不变（LTI）常系数微分方程。

2.微分方程的解

既然将线性系统的响应转换为微分方程的解，那么求解微分方程就是最重要的任务了！

Ⅰ.经典解

首先看一下微分方程的经典解：完全解=齐次解+特解

齐次解仅仅取决于系统本身，特解仅仅取决于激励。

Ⅱ.完全响应

系统的响应，就是完全响应，可以分为零状态响应和零输入响应，如图：

实际上，我们分析一个系统的响应，主要是从零输入响应和零状态响应入手的。

3.零输入响应

在零输入条件下，系统的响应就是零输入响应。
零输入条件下，微分方程等式右边都为0，化为齐次方程，求出特征根，就可以求出零输入响应！
当特征根都为单根时，零输入响应如下：

4.零状态响应

在零状态条件下，系统的响应就是零状态响应。
零状态条件下，初始状态都为0，即y(0-)=0…等等，此时的微分方程为非齐次方程，求出特征根，就可以求出零状态响应！
当特征根都为单根时，零状态响应如下：

利用卷积求零状态响应

5.冲激响应

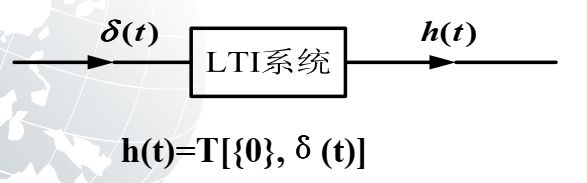
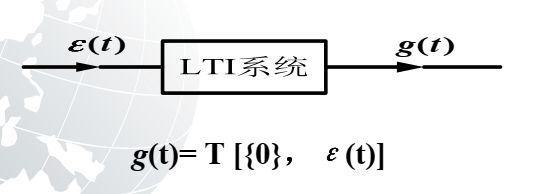
冲激响应是一种特殊的零状态响应，LTI系统处于零状态下，由单位冲激信号引起的响应就是冲激响应，一般用h(t)表示，冲激响应在后面求LTI系统响应的时候十分重要！！！
看一下冲激响应的框图表示：

6.阶跃响应

阶跃响应也是一种特殊的零状态响应，是输入为阶跃函数时系统的响应：

7.卷积求零状态响应

卷积的定义：

卷积的表示：

卷积的物理含义：

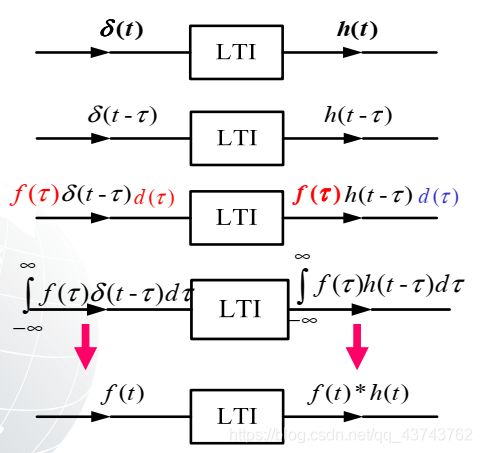
卷积求零状态响应：

任意信号都可以表示为冲激序列之和，所以，任意信号作用域系统的零状态响应都可以用冲激响应表示出来，这就是卷积求零状态响应：

二.连续信号的MATLAB描述

刚才已经对求解线性系统做了一个概括，那么各种函数是怎么样在MATLAB中描述的呢？接下来就一一介绍最常用的几种函数的MATLAB描述。
要知道，利用MATLAB分析连续信号时，要对信号作离散化处理，就是取出抽样点，根据抽样点的数据画出信号的图像，所以采样的区间和采样密度就影响着信号的表示效果。

1.单位冲激信号

MATLAB的实现代码如下：
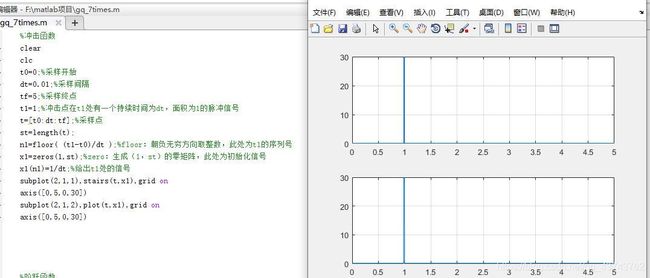
在MATLAB中，我们以持续时间为dt，面积为1的脉冲信号表示冲激函数，具体注释都已经在函数中作了描述：

冲击函数
clear
clc
t0=0;%采样开始
dt=0.01;%采样间隔
tf=5;%采样终点
t1=1;%冲击点在t1处有一个持续时间为dt，面积为1的脉冲信号
t=[t0:dt:tf];%采样点
st=length(t);
n1=floor( (t1-t0)/dt );%floor：朝负无穷方向取整数，此处为t1的序列号
x1=zeros(1,st);%zero：生成（1，st）的零矩阵，此处为初始化信号
x1(n1)=1/dt;%给出t1处的信号
subplot(2,1,1),stairs(t,x1),grid on
axis([0,5,0,30])
subplot(2,1,2),plot(t,x1),grid on
axis([0,5,0,30])

使用stairs和plot只是为了对比一下画图效果。
运行结果如示：

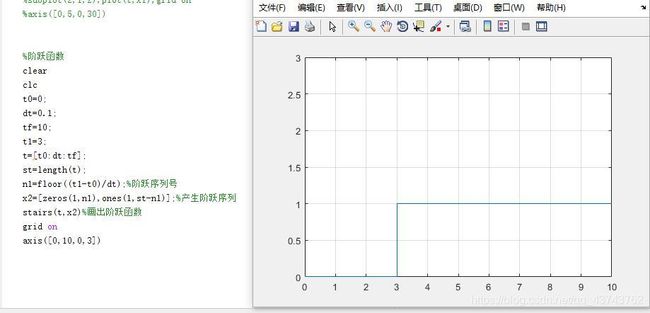
2.单位阶跃信号

代码如下：

clear
clc
t0=0;
dt=0.1;
tf=10;
t1=3;
t=[t0:dt:tf];
st=length(t);
n1=floor((t1-t0)/dt);%阶跃序列号
x2=[zeros(1,n1),ones(1,st-n1)];%产生阶跃序列
stairs(t,x2)%画出阶跃函数
grid on
axis([0,10,0,3])

运行结果如下：

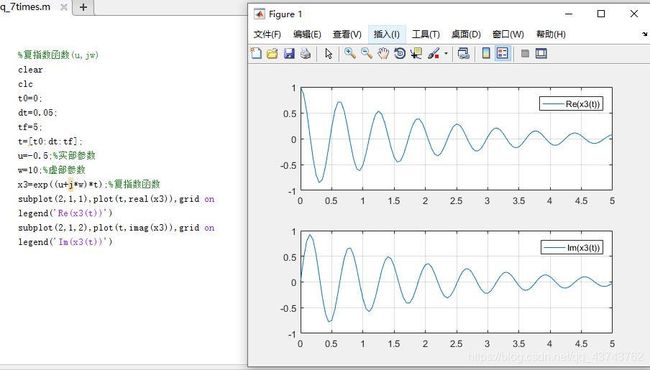
3.复指数信号

代码如下：

//复指数函数(u,jw)
clear
clc
t0=0;
dt=0.05;
tf=5;
t=[t0:dt:tf];
u=-0.5;%实部参数
w=10;%虚部参数
x3=exp((u+j*w)*t);%复指数函数
subplot(2,1,1),plot(t,real(x3)),grid on
legend('Re(x3(t))')
subplot(2,1,2),plot(t,imag(x3)),grid on
legend('Im(x3(t))')

运行结果如下：

三.LTI系统的零输入响应

零输入响应是微分方程的齐次解，具体讲解看下面吧（博主水平太低，讲不出来那种效果哈哈哈）

//LTI零输入响应
clear
clc
a=input('输入分母系数向量a=[a1,a2,...]=');%微分方程系数，从左到右
n=length(a)-1;
dt=input('采样步长dt=');
tf=input('仿真时长tf=');
Y0=input('初始条件向量Y0=[y0,Dy0,D2y0...]=');%已知初始条件
%以下为通解
p=roots(a);%p是特征方程的根,也就是系统的极点，roots(a)用来求多项式a(x)的根
V=rot90(vander(p));%V=vander(p),V是范德蒙矩阵
c=V\Y0';%用范德蒙矩阵求对应于各极点的系数
t=[0:dt:tf];
y=zeros(1,length(t));
for k=1:n
   y=y+c(k)*exp(p(k)*t);
end
plot(t,y),grid on

roots(a)用来求多项式a(x)的根。

四.求LTI系统零状态响应

前面说了，求零状态响应，要利用激励卷积冲激响应得到零状态响应，所以要求零状态响应就先得掌握冲激响应和卷积。

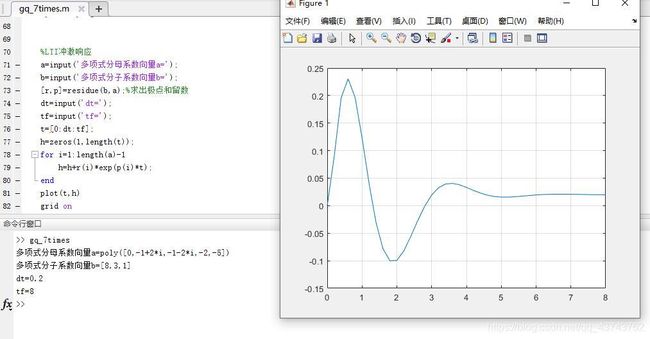
1.冲激响应

讲解直接上ppt吧：




直接上代码：

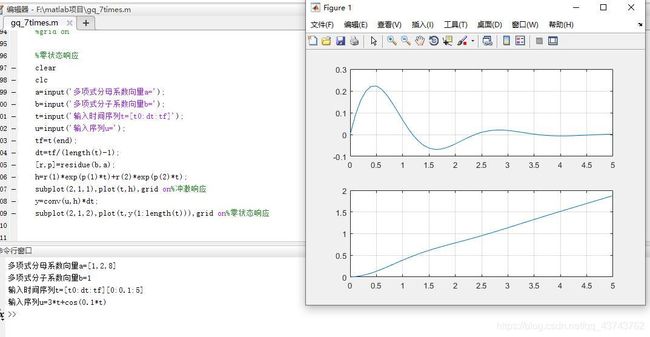
//LTI冲激响应
a=input('多项式分母系数向量a=');
b=input('多项式分子系数向量b=');
[r,p]=residue(b,a);%求出极点和留数
dt=input('dt=');
tf=input('tf=');
t=[0:dt:tf];
h=zeros(1,length(t));
for i=1:length(a)-1
    h=h+r(i)*exp(p(i)*t);
end
plot(t,h)%h冲激响应
grid on

运行结果如下：

2.卷积

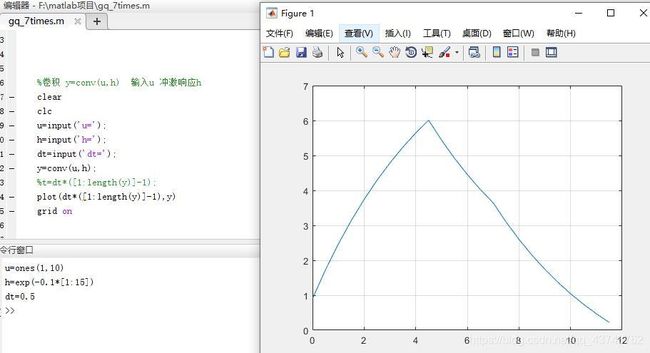
卷积很简单，MATLAB中利用函数conv(u,h)即可，意为求u、h的卷积：

//卷积 y=conv(u,h)  输入u 冲激响应h
lear
clc
u=input('u=');
h=input('h=');
dt=input('dt=');
y=conv(u,h);%进行卷积
%t=dt*([1:length(y)]-1);
plot(dt*([1:length(y)]-1),y)
grid on

3.卷积求零状态响应

这里就是重头戏啦！

• 先求冲激响应
• 再求卷积
• 得出零状态响应

如题：


实际上，如果单纯说使用matlab这个工具来求的时候，对原理不需要很深入的掌握，只要理解程序，会将程序套进去即可。
代码如下：（可以直接套的）

//零状态响应
clear
clc
a=input('多项式分母系数向量a=');%等式左边系数
b=input('多项式分子系数向量b=');%等式右边系数
t=input('输入时间序列t=[t0:dt:tf]');
u=input('输入序列u=');%输入函数
tf=t(end);
dt=tf/(length(t)-1);
[r,p]=residue(b,a);%用极点留数法求冲激响应
h=r(1)*exp(p(1)*t)+r(2)*exp(p(2)*t);%冲激响应
subplot(2,1,1),plot(t,h),grid on
y=conv(u,h)*dt;%用卷积求零状态响应
subplot(2,1,2),plot(t,y(1:length(t))),grid on%零状态响应

运行结果：

下面就试着用这个套路来做一道题：

可以看出：

• 多项式分母系数，也就是方程左边的系数为a=[1,4,3]
• 多项式分子系数，也就是方程右边的系数为b=1
• 然后就是构造单位阶跃函数
• 进行卷积

代码如下：

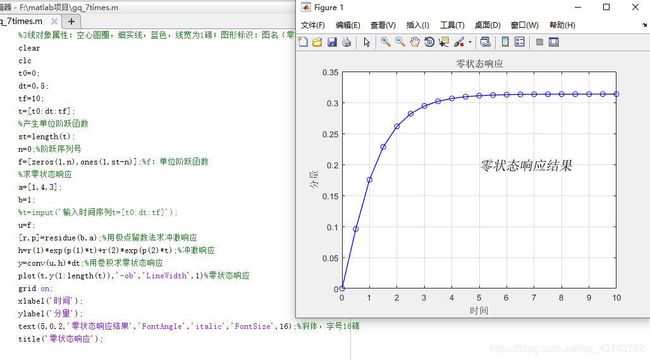
clear
clc
t0=0;
dt=0.5;
tf=10;
t=[t0:dt:tf];
%产生单位阶跃函数
st=length(t);
n=0;%阶跃序列号
f=[zeros(1,n),ones(1,st-n)];%f：单位阶跃函数
%求零状态响应
a=[1,4,3];
b=1;
%t=input('输入时间序列t=[t0:dt:tf]');
u=f;
[r,p]=residue(b,a);%用极点留数法求冲激响应
h=r(1)*exp(p(1)*t)+r(2)*exp(p(2)*t);%冲激响应
y=conv(u,h)*dt;%用卷积求零状态响应
plot(t,y(1:length(t)),'-ob','LineWidth',1)%零状态响应
grid on;
xlabel('时间');
ylabel('分量');
text(5,0.2,'零状态响应结果','FontAngle','italic','FontSize',16);%斜体，字号16磅
title('零状态响应');

运行结果如下：