精读《算法 - 动态规划》
很多人觉得动态规划很难,甚至认为面试出动态规划题目是在为难候选人,这可能产生一个错误潜意识:认为动态规划不需要掌握。
其实动态规划非常有必要掌握:
非常锻炼思维。动态规划是非常锻炼脑力的题目,虽然有套路,但每道题解法思路差异很大,作为思维练习非常合适。
非常实用。动态规划听起来很高级,但实际上思路和解决的问题都很常见。
动态规划用来解决一定条件下的最优解,比如:
自动寻路哪种走法最优?
背包装哪些物品空间利用率最大?
怎么用最少的硬币凑零钱?
其实这些问题乍一看都挺难的,毕竟都不是一眼能看出答案的问题。但得到最优解又非常重要,谁能忍受游戏中寻路算法绕路呢?谁不希望背包放的东西更多呢?所以我们一定要学好动态规划。
精读
动态规划不是魔法,它也是通过暴力方法尝试答案,只是方式更加 “聪明”,使得实际上时间复杂度并不高。
动态规划与暴力、回溯算法的区别
上面这句话也说明了,所有动态规划问题都能通过暴力方法解决!是的,所有最优解问题都可以通过暴力方法尝试(以及回溯算法),最终找出最优的那个。
暴力算法几乎可以解决一切问题。回溯算法的特点是,通过暴力尝试不同分支,最终选择结果最优的线路。
而动态规划也有分支概念,但不用把每条分支尝试到终点,而是在走到分叉路口时,可以直接根据前面各分支的表现,直接推导出下一步的最优解!然而无论是直接推导,还是前面各分支判断,都是有条件的。动态规划可解问题需同时满足以下三个特点:
存在最优子结构。
存在重复子问题。
无后效性。
存在最优子结构
即子问题的最优解可以推导出全局最优解。
什么是子问题?比如寻路算法中,走完前几步就是相对于走完全程的子问题,必须保证走完全程的最短路径可以通过走完前几步推导出来,才可以用动态规划。
不要小看这第一条,动态规划就难在这里,你到底如何将最优子结构与全局最优解建立上关系?
对于爬楼梯问题,由于每层台阶都是由前面台阶爬上来的,因此必然存在一个线性关系推导。
如果变成二维平面寻路呢?那么就升级为二维问题,存在两个变量
i,j与上一步之间关系了。如果是背包问题,同时存在物品数量
i、物品重量j和物品质量k三个变量呢?那就升级为三位问题,需要寻找三个之间的关系。
依此类推,复杂度可以上升到 N 维,维度越高思考的复杂度就越高,空间复杂度就越需要优化。
存在重复子问题
即同一个子问题在不同场景下存在重复计算。
比如寻路算法中,同样两条路线的计算中,有一段路线是公共的,是计算的必经之路,那么只算一次就好了,当计算下一条路时,遇到这个子路,直接拿第一次计算的缓存即可。典型例子是斐波那契数列,对于 f(3) 与 f(4),都要计算 f(1) 与 f(2),因为 f(3) = f(2) + f(1),而 f(4) = f(3) + f(2) = f(2) + f(1) + f(2)。
这个是动态规划与暴力解法的关键区别,动态规划之所以性能高,是因为 不会对重复子问题进行重复计算,算法上一般通过缓存计算结果或者自底向上迭代的方式解决,但核心是这个场景要存在重复子问题。
当你觉得暴力解法可能很傻,存在大量重复计算时,就要想想是哪里存在重复子问题,是否可以用动态规划解决了。
无后效性
即前面的选择不会影响后面的游戏规则。
寻路算法中,不会因为前面走了 B 路线而对后面路线产生影响。斐波那契数列因为第 N 项与前面的项是确定关联,没有选择一说,所以也不存在后效性问题。
什么场景存在后效性呢?比如你的人生是否能通过动态规划求最优解?其实是不行的,因为你今天的选择可能影响未来人生轨迹,比如你选择了计算机这个职业,会直接影响到工作的领域,接触到的人,后面的人生路线因此就完全变了,所以根本无法与选择了土木工程的你进行比较,因为人生赛道都变了。
有同学可能觉得这样局限是不是很大?其实不然,无后效性的问题仍然很多,比如背包放哪件物品、当前走哪条路线、用了哪些零钱,都不会影响整个背包大小、整张地图的地形、以及你最重要付款的金额。
解法套路 - 状态转移方程
解决动态规划问题的核心就是写出状态转移方程,所谓状态转移,即通过某些之前步骤推导出未来步骤。
状态转移方程一般写为 dp(i) = 一系列 dp(j) 的计算,其中 j < i。
其中 i 与 dp(i) 的含义很重要,一般 dp(i) 直接代表题目的答案,i 就有技巧了。比如斐波那契数列,dp(i) 表示的答案就是最终结果,i 表示下标,由于斐波那契数列直接把状态转移方程告诉你了 f(x) = f(x-1) + f(x-2),那么根本连推导都不必了。
对于复杂问题,难在如何定义 i 的含义,以及下一步状态如何通过之前状态推导。 这个做多了题目就有体会,如果没有,那即便再如何解释也难以说明,所以后面还是直接看例子吧。
先举一个最简单的动态规划例子 - 爬楼梯来说明问题。
爬楼梯问题
爬楼梯是一道简单题,题目如下:
假设你正在爬楼梯。需要
n阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?(给定n是一个正整数)
首先 dp(i) 就是问题的答案(解法套路,dp(i) 大部分情况就是答案,这样解题思路会最简化),即爬到第 i 阶台阶的方法数量,那么 i 自然就是要爬到第几阶台阶。
我们首先看是否存在 最优子结构?因为只能往上爬,所以第 i 阶台阶有几种爬方完全取决于前面有几种爬方,而一次只能爬 1 或 2 个台阶,所以第 i 阶台阶只可能从第 i-1 或 i-2 个台阶爬上来的,所以第 i 个台阶的爬法就是 i-1 与 i-2 总爬法之和。所以显然有最优子结构,连状态转移方程都呼之欲出了。
再看是否存在 存在重复子问题,其实爬楼梯和斐波那契数列类似,最终的状态转移方程是一样的,所以显然存在重复子问题。当然直观来看也容易分析出,10 阶台阶的爬法包含了 8、9 阶的爬法,而 9 阶台阶爬法包含了 8 阶的,所以存在重复子问题。
最后看是否 无后效性?由于前面选择一次爬 1 个或 2 个台阶并不会影响总台阶数,也不会影响你下一次能爬的台阶数,所以无后效性。如果你爬了 2 个台阶,因为太累,下次只能爬 1 个台阶,就属于有后效性了。或者只要你一共爬了 3 次 2 阶,就会因为太累而放弃爬楼梯,直接下楼休息,那么问题提前结束,也属于有后效性。
所以爬楼梯的状态转移方程为:
dp(i) = dp(i-1) + dp(i-2)dp(1) = 1dp(2) = 2
注意,因为 1、2 阶台阶无法应用通用状态转移方程,所以要特殊枚举。这种枚举思路在代码里其实就是 递归终结条件,也就是作为函数 dp(i) 不能无限递归,当 i 取值为 1 或 2 时直接返回枚举结果(对这道题而言)。所以在写递归时,一定要优先写上递归终结条件。
然后我们考虑,对于第一阶台阶,只有一种爬法,这个没有争议吧。对于第二阶台阶,可以直接两步跨上来,也可以走两个一步,所以有两种爬法,也很容易理解,到这里此题得解。
关于代码部分,仅这道题写一下,后面的题目如无特殊原因就不写代码了:
function dp(i: number) {
switch (i) {
case 1:
return 1;
case 2:
return 2;
default:
return dp(i - 1) + dp(i - 2);
}
}
return dp(n);
当然这样写重复计算了子结构,所以我们不要每次傻傻的执行 dp(i - 1)(因为这样计算了超多重复子问题),我们需要用缓存兜底:
const cache: number[] = [];
function dp(i: number) {
switch (i) {
case 1:
cache[i] = 1;
break;
case 2:
cache[i] = 2;
break;
default:
cache[i] = cache[i - 1] + cache[i - 2];
}
return cache[i];
}
// 既然用了缓存,最好子底向上递归,这样前面的缓存才能优先算出来
for (let i = 1; i <= n; i++) {
dp(i);
}
return cache[n];
当然这只是简单的一维线性缓存,更高级的缓存模式还有 滚动缓存。我们观察发现,这道题缓存空间开销是 O(n),但每次缓存只用了上两次的值,所以计算到 dp(4) 时,cache[1] 就可以扔掉了,或者说,我们可以滚动利用缓存,让 cache[3] 占用 cache[1] 的空间,那么整体空间复杂度可以降低到 O(1),具体做法是:
const cache: [number, number] = [];
function dp(i: number) {
switch (i) {
case 1:
cache[i % 2] = 1;
break;
case 2:
cache[i % 2] = 2;
break;
default:
cache[i % 2] = cache[(i - 1) % 2] + cache[(i - 2) % 2];
}
return cache[i % 2];
}
for (let i = 1; i <= n; i++) {
dp(i);
}
return cache[n % 2];
通过取余,巧妙的让缓存永远交替占用 cache[0] 与 cache[1],达到空间利用最大化。当然,这道题因为状态转移方程是连续用了前两个,所以可以这么优化,如果遇到用到之前所有缓存的状态转移方程,就无法使用滚动缓存方案了。然而还有更高级的多维缓存,这个后面提到的时候再说。
接下来看一个进阶题目,最大子序和。
最大子序和
最大子序和是一道简单题,题目如下:
给定一个整数数组
nums,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
首先按照爬楼梯的套路,dp(i) 就表示最大和,由于整数数组可能存在负数,所以越多数相加,和不一定越大。
接着看 i,对于数组问题,大部分 i 都可以代表以第 i 位结尾的字符串,那么 dp(i) 就表示以第 i 位结尾的字符串的最大和。
可能你觉得以 i 结尾,就只能是 [0-i] 范围的值,那么 [j-i] 范围的字符串不就被忽略了?其实不然,[j-i] 如果是最大和,也会被包含在 dp(i) 里,因为我们状态转移方程可以选择不连上 dp(i-1)。
现在开始解题:首先题目是最大和的连续子数组,一般连续的都比较简单,因为对于 dp(i),要么和前面连上,要么和前面断掉,所以状态转移方程为:
dp(i) = dp(i-1) + nums[i]如果dp(i-1) > 0。dp(i) = nums[i]如果dp(i-1) <= 0。
怎么理解呢?就是第 i 个状态可以直接由第 i-1 个状态推导出来,既然 dp(i) 是指以第 i 个字符串结尾的最大和,那么 dp(i-1) 就是以第 i-1 个字符串结尾的最大和,而且此时 dp(i-1) 已经算出来了,那么 dp(i) 怎么推导就清楚了:
因为字符串是连续的,所以 dp(i) 要么是 dp(i-1) + nums[i],要么就直接是 nums[i],所以选择哪种,取决于前面的 dp(i-1) 是否是正数,因为以 i 结尾一定包含 nums[i],所以 nums[i] 不管是正还是负,都一定要带上。 所以容易得知,dp(i-1) 如果是正数就连起来,否则就不连。
好了,经过这么详细的解释,相信你已经完全了解动态规划的解题套路,后面的题目解释方式我就不会这么啰嗦了!
这道题如果再复杂一点,不连续怎么办呢?让我们看看最长递增子序列问题吧。
最长递增子序列
最长递增子序列是一道中等题,题目如下:
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。
其实之前的 精读《DOM diff 最长上升子序列》 有详细解析过这道题,包括还有更优的贪心解法,不过我们这次还是聚焦在动态规划方法上。
这道题与上一道的区别就是,首先递增,其次不连续。
按照套路,dp(i) 就表示以第 i 个字符串结尾的最长上升子序列长度,那么重点是,dp(i) 怎么通过之前的推导出来呢?
由于是不连续的,因此不能只看 dp(i-1) 了,因为 nums[i] 项与 dp(j)(其中 0 <= j < i)组合后都可能达到最大长度,因此需要遍历所有 j,尝试其中最大长度的组合。
所以状态转移方程为:
dp[i] = max(dp[j]) + 1,其中 0<=jnum[j]
这道题的出现,预示着较为复杂的状态转移方程的出现,即第 i 项不是简单由 i-1 推导,而是由之前所有 dp(j) 推导,其中 0<=j
除此之外,还有推导变种,即根据 dp(dp(i)) 推导,即函数里套函数,这类问题由于加深了一层思考脑回路,所以相对更难。我们看一道这样的题目:最长有效括号。
最长有效括号
最长有效括号是道困难题,题目如下:
给你一个只包含
'('和')'的字符串,找出最长有效(格式正确且连续)括号子串的长度。
这道题之所以是困难题,就因为状态转移方程存在嵌套思维。
我们首先按套路定义 dp(i) 为答案,即以第 i 下标结尾的字符串中最长有效括号长度。看出来了吗?一般字符串题目中,i 都是以字符串下标结尾来定义,很少有定义为开头或者别的定义行为。当然非字符串问题就不是这样了,这个在后面再说。
我们继续题目,如果 s[i] 是 (,那么不可能组成有效括号,因为最右边一定不闭合,所以考虑 s[i] 为 ) 的场景。
如果 s[i-1] 为 (,那么构成了 ...() 之势,最后两个自成合法闭合,所以只要看前面的即可,即 dp(i-2),所以这种场景的状态转移方程为:
dp(i) = dp(i-2) + 2
如果 s[i-1] 是 ) 呢?构成了 ...)) 的状态,那么只有 i-1 是合法闭合的,且这个合法闭合段之前必须是 ( 与第 i 项形成闭合,才构成此时最长有效括号长度,所以这种场景的状态转移方程为:
dp(i) = dp(i-1) + dp(i - dp(i-1) - 2) + 2,你可以结合下面的图来理解:
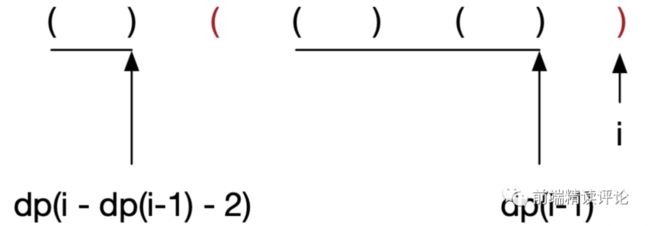
可以看到,dp(i-1) 就是第二条横线的长度,然后如果红色括号匹配的话,长度又 +2,最后别忘了最左边如果有满足匹配的也要带上,这就是 dp(i - dp(i-1) - 2),所以加到一起就是这种场景的括号最大长度。
到这里,一维动态规划问题深度基本上探索完了,在进入多维动态规划问题前,还有一类一维动态规划问题,属于表达式不难,也没有这题这么复杂的嵌套 DP,但是思维复杂度极高,你一定不要盯着全流程看,那样复杂度太高,你需要充分认可 dp(i-x) 已经算出来部分的含义,进行高度抽象的思考。
栅栏涂色
栅栏涂色是一道困难题,题目如下:
有
k种颜色的涂料和一个包含n个栅栏柱的栅栏,每个栅栏柱可以用其中一种颜色进行上色。你需要给所有栅栏柱上色,并且保证其中相邻的栅栏柱 最多连续两个 颜色相同。然后,返回所有有效涂色的方案数。
这道题 k 和 n 都非常巨大,常规暴力解法甚至普通 DP 都会超时。选择 i 的含义也很重要,这里 i 到底代表用几种颜色还是几个栅栏呢?选择栅栏会好做一些,因为栅栏是上色的主体。这样 dp(i) 就表示上色前 i 个栅栏的所有涂色方案。
首先看下递归终止条件。由于最多连续两个颜色相同,因此 dp(0) 与 dp(1) 分别是 k 与 k*k,因为每个栅栏随便刷颜色,自由组合。那么 dp(2) 有三个栅栏,非法情况是三个栅栏全同色,所以用所有可能减掉非法即可,非法场景只有 k 中,所以结果是 k*k*k - k。
那么考虑一般情况,对于 dp(i) 有几种涂色方案呢?直接思考情况太多,我们把情况一分为二,考虑 i 与 i-1 颜色相同与不同两种情况考虑。
如果 i 与 i-1 颜色相同,那么为了合法,i-1 肯定不能与 i-2 颜色相同了,否则就三个同色,这样的话,不管 i-2 是什么颜色,i-1 与 i 都只能少取一种颜色,少取的颜色就是 i-2 的颜色,因此 [i-1,i] 这个区间有 k-1 中取色方案,前面有 dp(i-2) 种取色方案,相乘就是最终方案数:dp(i-2) * (k-1)。
这背后其实存在动态思维,即每种场景的 k-1 都是不同的颜色组合,只是无论前面 dp(i-2) 是何种组合,后面两个栅栏一定有 k-1 种取法,虽然颜色组合的色值不同,但颜色组合数量是不变的,所以可以统一计算。理解这一点非常关键。
如果 i 与 i-1 颜色不同,那么第 i 项只有 k-1 种取法,一样也是动态的,因为永远不能和 i-1 颜色相同。最后乘上 dp(i-1) 的取色方案,就是总方案数:dp(i-1) * (k-1)。
所以最后总方案数就是两者之和,即 dp(i) = dp(i-2) * (k-1) + dp(i-1) * (k-1)。
这道题的不同之处在于,变化太多,任何一个栅栏取的颜色都会影响后面栅栏要取的颜色,乍一看觉得是个有后效性的题目,无法用动态规划解决。但实际上,虽然有后效性,但如果进行合理的拆解,后面栅栏的总可能性 k-1 是不变的,所以考虑总可能性数量,是无后效性的,因此站在方案总数上进行抽象思考,才可能破解此题。
接下来介绍多维动态规划,从二维开始。二维动态规划就是用两个变量表示 DP,即 dp(i,j),一般在二维数组场景出现较多,当然也有一些两个数组之间的关系,也属于二维动态规划,为了继续探讨字符串问题,我选择了字符串问题的二维动态规划范例,编辑距离这道题来说明。
编辑距离
编辑距离是一道困难题,题目如下:
给你两个单词
word1和word2,请你计算出将word1转换成word2所使用的最少操作数。你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
只要是字符串问题,基本上 i 都表示以第 i 项结尾的字符串,但这道题有两个单词字符串,为了考虑任意匹配场景,必须用两个变量表示,即 i j 分别表示 word1 与 word2 结尾下标时,最少操作次数。
那么对于 dp(i,j) 考虑 word1[i] 与 word2[j] 是否相同,最后通过双重递归,先递归 i,在递归内再递归 j,答案就出来了。
假设最后一个字符相同,即 word1[i] === word2[j] 时,由于最后一个字符不用改就相同了,所以操作次数就等价于考虑到前一个字符,即 dp(i,j) = dp(i-1,j-1)
假设最后一个字符不同,那么 最后一步 有三种模式可以得到:
假设是替换,即
dp(i,j) = dp(i-1,j-1) + 1,因为替换最后一个字符只要一步,并且和前面字符没什么关系,所以前面的最小操作次数直接加过来。假设是插入,即
word1插入一个字符变成word2,那么只要变换到这一步再 +1 插入操作就行了,变换到这一步由于插入一个就行了,因此word1比word2少一个单词,其它都一样,要变换到这一步,就要进行dp(i,j-1)的变换,因此dp(i,j) = dp(i,j-1) + 1。。假设是删除,即
word1删除一个字符变成word2,同理,要进行dp(i-1,j)的变化后多一步删除,因此dp(i,j) = dp(i-1,j) + 1。
由于题目取操作最少次数,所以这三种情况取最小即可,即 dp(i,j) = min(dp(i-1,j-1), dp(i,j-1), dp(i-1,j)) + 1。
所以同时考虑了最后一个字符是否相同后,合并了的状态转移方程就是最终答案。
我们再考虑终止条件,即 i 或 j 为 -1 时的情况,因为状态转移方程 i 和 j 不断减小,肯定会减少到 0 或 -1,因为 0 是字符串还有一个字符,相对比如考虑 -1 字符串为空时方便,因此我们考虑 -1 时作为边界条件。
当 i 为 -1 时,即 word1 为空,此时要变换为 word2 很显然,只有插入 j 次是最小操作次数,因此此时 dp(i,j) = j;同理,当 j 为 -1 时,即 word2 为空,此时要删除 i 次,因此操作次数为 i,所以 dp(i,j) = i。
非字符串问题
说到这,相信你在字符串动规问题上已经如鱼得水了,我们再看看非字符串场景的动规问题。非字符串场景的动规比较经典的有三个,第一是矩形路径最小距离,或者最大收益;第二是背包问题以及变种;第三是打家劫舍问题。
这些问题解决方式都一样,只是对于 dp(i) 的定义略有区别,比如对于矩形问题来说,dp(i,j) 表示走到 i,j 格子时的最小路径;对于背包问题,dp(i,j) 表示装了第 i 个物品时,背包还剩 j 空间时最大价格;对于打家劫舍问题,dp(i) 表示打劫到第 i 个房间时最大收益。
因为篇幅问题这里就不一详细介绍了,只简单说明一下矩形问题于打家劫舍问题。
对于矩形问题,状态转移方程重点看上个状态是如何转移过来的,一般矩形只能向右或者向下移动,路途可能有一些障碍物不能走,我们要做分支判断,然后选择一条符合题目最值要求的路线作为当前 dp(i) 的转移方程即可。
对于打家劫舍问题,由于不能同时打劫相邻的房屋,所以对于 dp(i),要么为了打劫 i-1 而不打劫第 i 间,或者打劫 i-2 于第 i 间,取这两种终态的收益最大值即可,即 dp(i) = max(dp(i-1), dp(i-2) + coins[i])。
总结
动态规划的核心分为三步,首先定义清楚状态,即 dp(i) 是什么;然后定义状态转移方程,这一步需要一些思考技巧;最后思考验证一下正确性,即尝试证明你写的状态转移方程是正确的,在这个过程要做到状态转移的不重不漏,所有情况都被涵盖了进来。
动态规划最经典的还是背包问题,由于篇幅原因,可能下次单独出一篇文章介绍。
讨论地址是:精读《算法 - 动态规划》· Issue #327 · dt-fe/weekly
如果你想参与讨论,请 点击这里,每周都有新的主题,周末或周一发布。前端精读 - 帮你筛选靠谱的内容。
关注 前端精读微信公众号

版权声明:自由转载-非商用-非衍生-保持署名(创意共享 3.0 许可证)