00- 深度学习之TensorFlow (综述2)

知识要点

• tf.keras.layers.Dense(32, activation="relu")    # 全连接层，输出最后一维维度为32，激活函数为relu，输出形状为(None, 32, 32).

---

三 TensorFlow的使用

神经网络的类型:     # 3种重要类型的神经网络，它们构成了深度学习中大多数预训练模型的基础

• 多层感知器: Multi-Layer Perceptron (MLP) / 人工神经网络Artificial Neural Networks (ANN)
• 卷积神经网络: Convolution Neural Networks (CNN)
• 循环神经网络: Recurrent Neural Networks (RNN)

3.1 神经网络详解

3.1.1 简介

• 机器学习需要进行特征提取, 深度学习不需要人工提取特征, 适合难提取特征的图像, 语音等.
• 深度学习算法试图从数据中学习高级功能，这是深度学习的一个非常独特的部分。因此，减少了为每个问题开发新特征提取器的任务。适合用在难提取特征的图像、语音、自然语言领域(NLP) 。
• 深度学习应用场景:  图像识别 (计算机视觉), 自然语言处理技术, 语音技术.
• 经典的神经网络结构: MLP由三层组成——输入层、隐藏层和输出层。
• RNN出现的目的是来处理序列数据的,  RNN在隐藏状态上有一个循环连接，此循环约束能够确保在输入数据中捕捉到顺序信息。循环神经网络能够帮助我们解决以下相关问题。
• CNN是 在空间上共享参数，RNN是在时间上共享参数。

3.1.2 神经网络基础

• Logistic回归: 逻辑回归是一个主要用于二分类的算法。
• 梯度下降算法:
  • 目的：使损失函数的值找到最小值.
  • 函数的梯度（gradient）指出了函数的最陡增长方向。
• 向量化的好处, 不用对每个特征都使用for循环, 速度更快. 
• 激活函数的选择: tanh 函数, ReLU 函数, Leaky ReLU.

3.2 梯度下降优化

优化遇到的问题, 梯度消失或者梯度爆炸, 局部最优.

1. 梯度下降算法的三种方式:

• 批量梯度下降法(batch)，即同时处理整个训练集.  # 当样本数在2000 以下时使用
• 小批量梯度下降法（Mini-Batch ）每次同时处理固定大小的数据集.  # 当训练样本较大时使用
• 随机梯度下降法（stochastic gradient descent）, 每次随机选一个进行处理.

2.数据预处理的方式:

• 指数加权平均（Exponentially Weight Average）: S_{2} = 0.9 S_{1} + 0.1 Y_{2}
• 动量梯度下降法（Gradient Descent with Momentum）: 计算梯度的指数加权平均数，并利用该值来更新参数值。
• RMSProp算法: 是在对梯度进行指数加权平均的基础上，引入平方和平方根。
• Adam算法: 将 Momentum 和 RMSProp 算法结合在一起。

3. 对网络输入的特征进行标准化，能够缓解梯度消失或者梯度爆炸.

4. 学习率衰减: 如果随着时间慢慢减少学习率 α 的大小, 有助于算法的收敛, 更容易接近最优解.

3.3 正则化

3.3.1 偏差和方差

“偏差-方差分解”（bias-variance decomposition）是解释学习算法泛化性能的一种重要工具。泛化误差可分解为偏差、方差与噪声，泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。

• 偏差：度量了学习算法的期望预测与真实结果的偏离程度, 即刻画了学习算法本身的拟合能力.
• 方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响.
• 噪声：表达了在当前任务上任何学习算法所能够达到的期望泛化误差的下界，即刻画了学习问题本身的难度.

对于高方差(过拟合)，有以下几种方式：

• 获取更多的数据，使得训练能够包含所有可能出现的情况

• 正则化（Regularization）

• 寻找更合适的网络结构

对于高偏差(欠拟合)，有以下几种方式：

• 扩大网络规模，如添加隐藏层或者神经元数量

• 寻找合适的网络架构，使用更大的网络结构，如AlexNet

• 训练时间更长一些

3.3.2 正则化

正则化，即在损失函数中加入一个正则化项(惩罚项)，惩罚模型的复杂度，防止网络过拟合.

逻辑回归的L1与L2正则化:

• L1是直线距离, L2是平方再开方
• 正则化项的理解: 在损失函数中增加一项，那么其实梯度下降是要减少损失函数的大小，对于L2或者L1来讲都是要去减少这个正则项的大小，那么也就是会减少W权重的大小。这是我们一个直观上的感受。

神经网络中的正则化: 神经网络中的正则化与逻辑回归相似，只不过参数W变多了，每一层都有若干个权重，可以理解成一个矩阵。

• 正则化为什么能够防止过拟合: 正则化因子设置的足够大的情况下，为了使成本函数最小化，权重矩阵 W 就会被设置为接近于 0 的值，直观上相当于消除了很多神经元的影响，那么大的神经网络就会变成一个较小的网络。
• Dropout正则化: 随机丢弃神经网络中的部分神经元操作。
  • Inverted droupout: 训练的时候只有占比为pp的隐藏层单元参与训练。增加最后一行代码的原因，在预测的时候，所有的隐藏层单元都需要参与进来，就需要测试的时候将输出结果除以以pp使下一层的输入规模保持不变。

3.3.3 其它正则化方法

• 早停止法（Early Stopping）: 通常不断训练之后，损失越来越小。但是到了一定之后，模型学到的过于复杂（过于拟合训练集上的数据的特征）造成测试集开始损失较小，后来又变大。模型的w参数会越来越大，那么可以在测试集损失减小一定程度之后停止训练。
• 数据增强: 指通过剪切、旋转/反射/翻转变换、缩放变换、平移变换、尺度变换、对比度变换、噪声扰动、颜色变换等一种或多种组合数据增强变换的方式来增加数据集的大小。
  • 离线增强。预先进行所有必要的变换，从根本上增加数据集的规模。
  • 在线增强，或称为动态增强。可通过对即将输入模型的小批量数据的执行相应的变化，这样同一张图片每次训练被随机执行一些变化操作，相当于不同的数据集了。

3.4 tensorflow 基础操作

TensorFlow是深度学习领域使用最为广泛的一个Google的开源软件库. 定义的数据叫做Tensor(张量), Tensor又分为常量和变量.

3.4.1 常量操作

常量一旦定义值不能改变: t = tf.constant([[1., 2., 3.], [4., 5., 6.]])   # 部分常量的操作

• print(t+10)       # 每个元素都加10
• print(tf.square(t))       # 每个元素都做平方
• print(t @ tf.transpose(t))       # @表示矩阵的点乘
• 常量tensor和numpy中的ndarray的转化: tf.constant(numpy)     # 将numpy数组转换为tensor
• 可以直接切片: t[:, 1:].numpy()  
• 使用字符串数组:       # d = tf.constant("cafe")     # strings
  • 字符串的一些方法: tf.strings.length(d)
  • utf8的编码长度: tf.strings.length(d, unit = 'UTF8_CHAR')
  • 字符编码方式的转化: tf.strings.unicode_decode(d, 'UTF8')

3.4.2 不整齐的tensor

创建ragged tensor:     # ragged tensor 不整齐的tensor, 上面的tensor每个字符串长度不一致.

•  创建ragged: r = tf.ragged.constant([[11, 12], [21, 22, 23], [], [41]])
• 拼接张量的函数: print(tf.concat([r, r2], axis = 0))
• 按列拼接: print(tf.concat([r, r3], axis = 1))
• ragged tensor转化为普通tensor: print(r.to_tensor())  # 缺元素的地方补0, 0在正常元素的后面.
• s = tf.SparseTensor(indices = [[0, 1], [1, 0]], values = [1., 2.], dense_shape = [3, 4])   # 创建sparse tensor   # sparse tensor 稀疏 tensor, tensor中大部分元素是0, 少部分元素是非0.
• 把sparse tensor转化为稠密矩阵: print(tf.sparse.to_dense(s))    # 注意在定义sparse tensor的时候 indices 必须是排好序的. 如果不是, 定义的时候不会报错, 但是在to_dense的时候会报错.

3.4.3 变量的使用

变量定义之后可以改变值: v = tf.Variable([[1, 2, 4], [3, 5, 6]])

• 对变量之间赋值, 所有位置乘于2: v.assign(2*v)
• 对变量的某个位置进行赋值: v[0, 1].assign(42)
• 对变量的某一行赋值: v[1].assign([7, 8, 9])

3.4.4 TensorFlow的数学运算

定义运算, 也可以直接使用python运算符+,-, * / ...

• add = tf.add(a, b)
• sub = tf.subtract(a, b)
• mul = tf.multiply(a, b)
• div = tf.divide(a, b)

聚合运算: 用于计算张量tensor沿着指定的数轴上的的平均值: tf.reduce_mean(x)

• 默认会聚合所有的维度:  x_mean = tf.reduce_mean(x)    # x = np.random.randint(0,10, size=(3,6))
• 按列求和: print(x.sum(axis = 0))
• 可以指定聚合的轴: x_reduce_mean = tf.reduce_mean(x, axis=0)

矩阵运算:

• dot = tf.matmul(x, y)      # 矩阵乘法的简写: x @ y

3.5 TensorFlow实现线性回归和逻辑回归

实现一个算法主要从以下三步入手:     # 逻辑角度

• 找到这个算法的预测函数, 比如线性回归的预测函数形式为:y = wx + b,
• 找到这个算法的损失函数 , 比如线性回归算法的损失函数为最小二乘法
• 找到让损失函数求得最小值的时候的系数, 这时一般使用梯度下降法.

使用TensorFlow实现算法的基本套路:

• 使用TensorFlow中的变量将算法的预测函数, 损失函数定义出来.    # w, b
• 使用梯度下降法优化器求损失函数最小时的系数
• 分批将样本数据投喂给优化器,找到最佳系数

3.5.1 线性回归

线性回归要点:

• 生成线性数据: x = np.linspace(0, 10, 20) + np.random.rand(20)
• 画点图: plt.scatter(x, y)
• TensorFlow定义变量: w = tf.Variable(np.random.randn() * 0.02)
• tensor 转换为 numpy数组: b.numpy()
• 定义优化器: optimizer = tf.optimizers.SGD()
• 定义损失:  tf.reduce_mean(tf.square(y_pred - y_true))   # 求均值
• 自动微分: tf.GradientTape()
• 计算梯度: gradients = g.gradient(loss, [w, b])
• 更新w, b: optimizer.apply_gradients(zip(gradients, [w, b]))

3.5.2 逻辑回归

• 查看安装文件: pip list
• 聚类数据生成器: make_blobs
• 生成聚类数据: data, target = make_blobs(centers = 3)
• 转换为tensor 数据: x = tf.constant(data, dtype = tf.float32)
• 定义tensor变量: B = tf.Variable(0., dtype = tf.float32)
• 矩阵运算: tf.matmul(x, W)
• 返回值长度为batch_size的一维Tensor: tf.sigmoid(linear)
• 调整形状: y_pred = tf.reshape(y_pred, shape = [100])
• tf.clip_by_value(A, min, max)：     # 输入一个张量A，把A中的每一个元素的值都压缩在min和max之间。
• 求均值: tf.reduce_mean()
• 定义优化器: optimizer = tf.optimizers.SGD()
• 计算梯度: gradients = g.gradient(loss, [W, B])    # with tf.GradientTape() as g
• 迭代更新W, B: optimizer.apply_gradients(zip(gradients, [W, B]))
• 准确率计算: (y_ == y_true).mean()

3.6 使用Keras创建模型

3.6.1 模型创建

1. 对于输入层,需要指定输入数据的尺寸,通过Dense对象中的input_shape属性.注意无需写batch的大小. input_shape=(784,)  等价于我们在神经网络中定义的shape为(None, 784)的Tensor.

2. 模型创建成功之后,需要进行编译.使用.compile()方法对创建的模型进行编译.compile()方法主要需要指定一下几个参数:

• 优化器 optimizer: 可以是Keras定义好的优化器的字符串名字,比如'rmsprop'也可以是Optimizer类的实例对象.常见的优化器有: SGD, RMSprop, Adagrad, Adadelta等.
• 损失函数 loss: 模型视图最小化的目标函数, 它可以是现有损失函数的字符串形式, 比如: categorical_crossentropy, 也可以是一个目标函数.  
• 评估标准 metrics. 评估算法性能的衡量指标.对于分类问题, 建议设置为metrics = ['accuracy'].评估标准可以是现有的标准的字符串标识符，也可以是自定义的评估标准函数。

3. 训练模型: 使用.fit()方法,将训练数据,训练次数(epoch), 批次尺寸(batch_size)传递给fit()方法.

4. 模型评估: 使用 tf.keras.Model.evaluate and tf.keras.Model.predict进行评估和预测. 评估会打印算法的损失和得分.

5. 函数式创建模型: 函数式API, 主要是需要自己把各个组件的对象定义出来, 并且手动传递.

6. 模型保存和恢复:

• 使用model.save把整个模型保存为HDF5文件.
• 恢复使用tf.keras.models.load_model即可.

3.6.2 模型创建命令

• 模型创建: model = Sequential()
• 添加卷积层: model.add(Dense(32, activation='relu', input_dim=100))  # 第一层需要 input_dim
• 添加dropout: model.add(Dropout(0.2))
• 添加全连接层: model.add(Dense(512, activation='relu'))   # 除了first, 其他层不要输入shape
• 添加输出层: model.add(Dense(num_classes, activation='softmax'))  # last 通常使用softmax
• TensorFlow 中，使用 model.compile() 方法来选择优化器和损失函数:
  • optimizer: 优化器: 主要有: tf.train.AdamOptimizer , tf.train.RMSPropOptimizer , or tf.train.GradientDescentOptimizer .
  • loss: 损失函数: 主要有:mean square error (mse, 回归), categorical_crossentropy (多分类) , and binary_crossentropy (二分类).
  • metrics: 算法的评估标准, 一般分类用accuracy.
• 模型显示: model.summary()
• model.fit(x_train, y_train, batch_size = 64, epochs = 20, validation_data = (x_test, y_test))    # 模型训练
• 模型评估: score = model.evaluate(x_test, y_test, verbose=0)   # 两个返回值: [损失率, 准确率]
• 保存模型: model.save('my_model.h5')
• 加载模型: model = tf.keras.models.load_model('my_model.h5')

面对大数据集处理:

• 把大数据集数据变成dataset: dataset = tf.data.Dataset.from_tensor_slices((data, labels))
  • 指定每批数据大小: dataset = dataset.batch(32).repeat()
  • dataset 数据训练: model.fit(dataset, epochs=10, steps_per_epoch=30)

3.6.3 模型优化进阶

• 导入数据: (x_train, y_train), (x_test, y_test) = mnist.load_data()
• x_train, x_valid, y_train, y_valid = train_test_split(x_train_all, y_train_all, random_state = 11)  # 数据拆分, 从x_train_all中切割出训练数据和校验数据
• 标准化处理:  x_train_scaled = scaler.fit_transform(x_train)          # scaler = StandardScaler()
• one-hot编码: y_train = tf.keras.utils.to_categorical(y_train, 10)
• 定义神经网络: model = tf.keras.Sequential()
• 第一层输入元组或数字: model.add(Dense(64, input_shape=(784)))
• 添加selu 层: model.add(Dense(64, activation='selu'))
• 添加激活层: model.add(Activation('relu'))
• 添加BN层: model.add(BatchNormalization())         # 优化算法: 1.最重要的作用是加快网络的训练和收敛的速度； 2.控制梯度爆炸防止梯度消失； 3.防止过拟合  # 先BN再激活比先激活再BN效果好一点 .
• 添加输出层: model.add(Dense(10, activation='softmax'))  输出层的激活, 二分类是sigmoid, 多分类的话是softmax .
  • softmax是个非常常用而且比较重要的函数，尤其在多分类的场景中使用广泛。他把一些输入映射为0-1之间的实数，并且归一化保证和为1，因此多分类的概率之和也刚好为1。
• model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])   # 配置网络
• Flatten层: model.add(Flatten(input_shape=(28, 28)))     # 即reshape, 展平
• 训练网络: model.fit(x_train_scaled, y_train, batch_size=64, epochs=5)
• 查看网络参数量: model.summary()
• 评估模型: model.evaluate(x_test_scaled, y_test)     # loss: 0.1095 - accuracy: 0.9761
• 保存模型: model.save('./model.h5')        # 只保存模型, 不保存参数
• 读取模型: model2 = tf.keras.models.load_model('./model.h5')
• 模型预测: model.predict(x_test)
• 随机丢弃神经网络: model.add(Dropout(0.2))
• model.add(AlphaDropout(0.2))  
  • AlphaDropout是一种保持 self-normalizing 属性的Dropout。对于一个0均值和单位标准差的输入，AphaDropout的输出保持输入的均值和标准差不变,  防止过拟合。
  •  AlphaDropout和SELU激活函数一起使用，保证了输出是0均值和单位标准差。
  • SELU激活函数是一种自归一化的神经网络的激活函数，它也是一种基于激活函数的正则化方案。  # 优点：在全连接层效果好，可以避免梯度消失和爆炸。
• l1_l2正则化: model.add(Dense(64, activation='relu', kernel_regularizer='l1_l2'))
  • 对于网络层 =+ ,他们的作用机制是相似的，区别是作用的对象不同， kernel_regularizer作用于权重，bias_regularizer作用于，而activity_regularizer则作用于该层的输出 .
• dataset: 通常用于训练数据和目标值的集合, 保存到一起. 可以直接传入model中.

tf.where(condition, x=None, y=None,name=None)

• condition: 一个 tensor, 数据类型为tf.bool/bool类型，condition是bool型值
• 返回值：如果x、y不为空的话，返回值和x、y有相同的形状，如果condition对应位置值为True那么返回Tensor对应位置为x的值，否则为y的值.

3.7 wide and deep模型

3.7.1 Wide and deep 模型

2014年提出的GoogLeNet模型使用该方式.

Wide and deep 模型是 TensorFlow 在 2016 年 6 月左右发布的一类用于分类和回归的模型，并应用到了 Google Play 的应用推荐中。wide and deep 模型的核心思想是结合线性模型的记忆能力（memorization）和 DNN 模型的泛化能力（generalization），在训练过程中同时优化 2 个模型的参数，从而达到整体模型的预测能力最优。

• 记忆（memorization）即从历史数据中发现item或者特征之间的相关性。
• 泛化（generalization）即相关性的传递，发现在历史数据中很少或者没有出现的新的特征组合。

多输入wide&deep模型:

• concat = keras.layers.concatenate([input_wide, hidden2])  # 定义两个输入创建模型,  然后其中一个进行深度卷积, 另一个直接用来结合卷积后的结果. 同时注意需要对输入特征数据进行调整.
• model = keras.models.Model(inputs=[input_wide,input_deep],outputs =[output,output2])  # 多输入输出

input = keras.layers.Input(shape = x_train.shape[1:])    # (11610, 8)
hidden1 = keras.layers.Dense(32, activation = 'relu')(input)
hidden2 = keras.layers.Dense(32, activation = 'relu')(hidden1)
 
concat = keras.layers.concatenate([input, hidden2])
output = keras.layers.Dense(1)(concat)
model = keras.models.Model(inputs = [input], outputs = output)

3.7.2 定义callback

• 回调函数中添加保存最佳参数的模型.
• 定义提前停止的条件    # 连续多少次变化幅度小于某值时停止训练

定义保存的文件夹:

• log_dir = './callback'   
• output_model_file = os.path.join(log_dir, 'model.h5')  

定义callback:

• callbacks = [
      keras.callbacks.TensorBoard(log_dir),
      keras.callbacks.ModelCheckpoint(output_model_file, save_best_only = True),
      keras.callbacks.EarlyStopping(patience = 5, min_delta = 1e-3)]

执行训练:

• history = model.fit(x_train_scaled,y_train,validation_data =(x_valid_scaled,y_valid),
                      epochs = 50, callbacks = callbacks)

3.7.3 函数构建模型

• 函数构建卷积后的结果结合原始输入进行运算.

class WideDeepModel(keras.models.Model):
    def __init__(self):
        '''定义模型的层次'''
        super().__init__()
        self.hidden1 = keras.layers.Dense(32, activation = 'relu')
        self.hidden2 = keras.layers.Dense(32, activation = 'relu')
        self.output_layer = keras.layers.Dense(1)
        
    def call(self, input):
        '''完成模型的正向传播'''
        hidden1 = self.hidden1(input)
        hidden2 = self.hidden2(hidden1)
        # 拼接
        concat = keras.layers.concatenate([input, hidden2])
        output = self.output_layer(concat)
        return output
    
'''定义实例对象'''
model = WideDeepModel()
model.build(input_shape = (None, 8))

model.compile(loss = 'mse', optimizer = 'adam', metrics = ['mse'])   # 模型配置
history = model.fit(x_train_scaled, y_train, validation_data = (x_valid_scaled, y_valid), epochs= 20)

3.8 超参数搜索

超参数搜索的方式: 网格搜索, 随机搜索, 遗传算法搜索, 启发式搜索.

超参数训练后用： gv.estimator 调取最佳模型.

3.8.1 函数定义模型

from tensorflow.keras.wrappers.scikit_learn import KerasRegressor   # 回归神经网络
# 搜索最佳学习率
def build_model(hidden_layers = 1, layer_size = 30, learning_rate = 3e-3):
    model = keras.models.Sequential()
    model.add(keras.layers.Dense(layer_size, activation = 'relu', input_shape = x_train.shape[1:]))
    for _ in range(hidden_layers - 1):
        model.add(keras.layers.Dense(layer_size, activation = 'relu'))
    model.add(keras.layers.Dense(1))
    optimizer = keras.optimizers.SGD(learning_rate)
    model.compile(loss = 'mse', optimizer = optimizer)
    # model.summary()
    return model
sklearn_model = KerasRegressor(build_fn = build_model)

3.8.2 超参数搜索

# 使用sklearn 的网格搜索, 或者随机搜索
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
params = {
    'learning_rate' : [1e-4, 3e-4, 1e-3, 3e-3, 1e-2, 3e-2],
    'hidden_layers': [2, 3, 4, 5], 
    'layer_size': [20, 60, 100]}
 
gv = GridSearchCV(sklearn_model, param_grid = params, n_jobs = 1, cv= 5,verbose = 1)
gv.fit(x_train_scaled, y_train)

• 调取最佳模型: print(gv.estimator)
• 最佳得分: print(gv.best_score_)      # -0.47164334654808043
• 最佳参数: print(gv.best_params_)   # {'hidden_layers': 5,'layer_size': 100,'learning_rate':0.01}

3.9 GPU设置和多分布自定义模型

3.9.1 GPU设置

• 显示数据所在的位置:  tf.debugging.set_log_device_placement(True)
• 显示电脑上的GPU: gpus = tf.config.experimental.list_physical_devices('GPU')
• 设置GPU具体哪一个可用: tf.config.experimental.set_visible_devices(gpus[0], 'GPU')

x_train_scaled = scaler.fit_transform(x_train.astype(np.float32).reshape(55000, -1))     # scaler = StandardScaler()   # 正则化需要先偏平化处理数据

3.9.2 设置模型在不同的GPU上运行

• 设置GPU: with tf.device(logical_gpus[0].name)

# 逻辑GPU
logical_gpus = tf.config.experimental.list_logical_devices('GPU')

model = keras.models.Sequential()
with tf.device(logical_gpus[0].name):
    model.add(keras.layers.Dense(512, activation = 'relu', input_shape = (784, )))
    model.add(keras.layers.Dense(512, activation = 'relu'))
    
with tf.device(logical_gpus[1].name):
    model.add(keras.layers.Dense(512, activation = 'relu'))
    model.add(keras.layers.Dense(512, activation = 'relu'))
 
    model.add(keras.layers.Dense(10, activation = 'softmax'))
 
model.compile(loss = 'sparse_categorical_crossentropy',
              optimizer = 'adam',
              metrics = ['accuracy'])

3.10 模型保存和加载

3.10.1 保存模型和加载

直接保存模型:

• 保存模型: model.save(os.path.join(logdir, 'fashion_mnist_model.h5'))   # logdir = './graph_def_and_weights'
• 加载模型: model2 = keras.models.load_model(os.path.join(logdir, 'fashion_mnist_model.h5'))
• 保存参数: model.save_weights(os.path.join(logdir, 'fashion_mnist_weights_2.h5'))
• 加载参数: model.load_weights( os.path.join(logdir, 'fashion_mnist_weights_2.h5'))

保存模型为savemodel格式:

• 保存成savedmodel格式: tf.saved_model.save(model, './keras_saved_model')
• 加载savedmodel模型: loaded_saved_model = tf.saved_model.load('./keras_saved_model')

3.11 卷积神经网络(CNN)的使用

卷积神经网络由一个或多个卷积层、池化层、全连接层及激活函数等组成, 与其他深度学习结构相比，卷积神经网络在图像等方面能够给出更好的结果。

感受野(receptive field): 在卷积神经网络中，决定某一层输出结果中一个元素所对应的输入层的区域大小，被称作感受野。通俗的解释，输出feature map上的一个单元对应输入层上的区域大小。

3.11.1 卷积层

目的: 卷积运算的目的是提取输入的不同特征，某些卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网路能从低级特征中迭代提取更复杂的特征。

参数：

• size: 卷积核/过滤器大小，选择有1 *1， 3* 3， 5 * 5, 卷积核通常为奇数进行卷积.
• padding：零填充，Valid 与Same  # 根据卷积核和步长确定在卷积前原图像周边进行0填充.
  • Valid: 不填充, 这样会导致图像变小和边缘信息丢失.   # 向上取整
  • Same：输出大小与原图大小一致, 根据卷积核和步长确定进行填充0的圈数.  # 向上取整
• stride: 步长，通常默认为1, 卷积核在图像上每次计算后移动的跨度.

3.11.2 池化层(Pooling)

池化层主要对卷积层学习到的特征图进行亚采样（subsampling）处理，主要由两种：

• 最大池化：Max Pooling, 取窗口内的最大值作为输出, 常用
• 平均池化：Avg Pooling, 取窗口内的所有值的均值作为输出

意义在于：

• 降低了后续网络层的输入维度，缩减模型大小，提高计算速度
• 提高了Feature Map 的鲁棒性，防止过拟合.

3.11.3 全连接层

卷积层+激活层+池化层可以看成是CNN的特征学习/特征提取层，而学习到的特征（Feature Map）最终应用于模型任务（分类、回归）, 需进行处理：

• 先对所有 Feature Map 进行扁平化（flatten, 即 reshape 成 1 x N 向量）
• 再接一个或多个全连接层，进行模型学习

3.11.4 图片卷积实操

• 均值滤波, 平滑处理.

# 均值滤波  # 平滑处理, 用卷积直接扫描
input_img = tf.constant(moon.reshape(1, 474, 630, 1), dtype = tf.float32)
filters = tf.constant(np.array([[1/9, 1/9, 1/9], [1/9, 1/9, 1/9], [1/9, 1/9, 1/9]]).reshape(3, 3, 1, 1),
                      dtype = tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input =  input_img, filters= filters, strides= strides, padding= 'SAME')
plt.figure(figsize= (10, 8))
plt.imshow(conv2d.numpy().reshape(474, 630), cmap = 'gray')

• filters = tf.constant(np.array([[1/9, 2/9, 1/9], [2/9, 3/9, 2/9], [1/9, 2/9, 1/9]]).reshape(3, 3, 1, 1), dtype = tf.float32)     # 高斯滤波卷积核
• filters = tf.constant(np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]]).reshape(3, 3, 1, 1), dtype = tf.float32)     # 边缘检测卷积核

3.12 比较著名的深度学习模型

3.12.1 AlexNet

AlexNet 是2012年ISLVRC 2012 竞赛的冠军网络，分类准确率由传统的 70%+提升到 80%+。它是由Hinton和他的学生Alex Krizhevsky设计的,  也是在那年之后，深度学习开始迅速发展。

该网络的亮点在于：

1. 首次利用 GPU 进行网络加速训练。
2. 使用了 ReLU 激活函数，而不是传统的 Sigmoid 激活函数以及 Tanh 激活函数。
3. 使用了 LRN 局部响应归一化。
4. 在全连接层的前两层中使用了 Dropout 随机失活神经元操作，以减少过拟合。

输入图片尺寸: input_size:  [224, 224, 3]

模型参数: 14601930

3.12.2 VGG

VGG在2014年由牛津大学著名研究组VGG提出，斩获该年ImageNet竞赛中 Localization Task (定位 任务) 第一名 和 Classification Task (分类任务) 第二名。

• 网络中的亮点：通过堆叠多个 3x3的卷积核 来替代大尺度卷积核（减少所需参数）.
• 模型继续变大, vgg16模型参数: 27828042, 效果更好的模型参数更多.
• 常见的vgg模型: vgg11, vgg13, vgg16, vgg19.

3.12.3 GoogLeNet

GoogLeNet在2014年由Google团队提出，斩获当年ImageNet竞赛中 Classification Task (分类任务) 第一名。

网络中的亮点：

• 引入了Inception结构（融合不同尺度的特征信息）    # 模块化
• 使用1x1的卷积核进行降维以及映射处理
• 添加两个辅助分类器帮助训练
• 丢弃全连接层，使用平均池化层（大大减少模型参数）
• GoogLeNet模型参数只有VGG的 1/20.
• 模型参数: 10334030

3.12.4 ResNet

ResNet在2015年由微软实验室提出，斩获当年ImageNet竞赛中分类任务第一名，目标检测第一名。获得COCO数据集中目标检测第一名，图像分割第一名。

网络中的亮点：

• 超深的网络结构 (突破1000层)
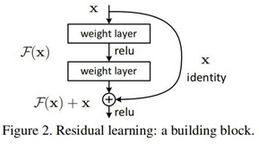
• 提出residual模块
• 使用Batch Normalization加速训练(丢弃dropout)
• 常见的restnet模型: restnet34, restnet50
• 模型参数: 21306826     # restnet34

residual结构:   # 标准模块

• 1x1的卷积核用来降维和升维

• 注意：主分支与shortcut的输出特征矩阵shape必须相同.

3.13 迁移学习

3.13.1 迁移学习方式

使用迁移学习的优势：

• 能够快速的训练出一个理想的结果
• 当数据集较小时也能训练出理想的效果.

常见的迁移学习方式：

1. 载入权重后训练所有参数.
2. 载入权重后只训练最后几层参数.
3. 载入权重后在原网络基础上再添加一层全连接层，仅训练最后一个全连接层.

3.13.2 迁移学习操作

导入resnet模型:       # 使用方式三

• model = keras.models.Sequential()      # 开始建模
• resnet50 = keras.applications.ResNet50(include_top=False, pooling='avg')      # 导入模型
• model.add(resnet50)      # 添加resnet 网络
• model.add(keras.layers.Dense(num_classes=10, activation = 'softmax'))     # 添加全连接层
• model.layers[0].trainable = False     # 除了最后一个全连接层, 其余部分参数不变
• model.compile(loss = 'categorical_crossentropy', optimizer = 'adam', metrics = ['acc'])   # 模型配置
• valid_datagen = keras.preprocessing.image.ImageDataGenerator(preprocessing_function = keras.applications.resnet50.preprocess_input)      # 数据初始化处理   # 使用别人预训练模型参数时，要注意别人的预处理方式

使用方式二: 指定不可调整层数:     # 训练后面几层神经网络参数

# 切片指定, 不可调整的层数
for layer in resnet50.layers[0:-5]:
    layer.trainable = False

3.14 MobileNet网络

3.14.1 MobileNet简介

MobileNet网络是由google团队在2017年提出的，专注于移动端或者嵌入式设备中的轻量级CNN网络。相比传统卷积神经网络，在准确率小幅降低的前提下大大减少模型参数与运算量。(相比VGG16准确率减少了0.9%， 但模型参数只有VGG的1/32)

MobileNet 网络中的亮点：

• Depthwise Convolution (大大减少运算量和参数数量)   # DW卷积
• 增加超参数α、β

卷积特征对比:

• 传统卷积:
  • 卷积核channel = 输入特征矩阵channel
  • 输出特征矩阵channel = 卷积核个数
• DW卷积:           # Depthwise Conv
  • 卷积核channel = 1
  • 输入特征矩阵channel = 卷积核个数 = 输出特征矩阵channel

3.14.2 MobileNet v2

MobileNet v2网络是由google团队在2018年提出的，相比MobileNet V1网 络，准确率更高，模型更小。

网络中的亮点：

• Inverted Residuals（倒残差结构）
• Linear Bottlenecks

3.14.3 MobileNet V3

网络中的亮点：

• 更新Block (bneck)
• 使用NAS搜索参数（Neural Architecture Search）
• 重新设计耗时层结构

• 重新设计激活函数: ReLU6(x)     # self.relu6 = layers.ReLU(6.)