支持向量机——SVM原理
SVM——Support Vector Machine
5.11 update:拉格朗日对偶问题的推导
5.15 update:SMO算法推导
5.17 update:sklearn实现
文章目录
- SVM——Support Vector Machine
-
- 简介
- 概念解释
- 基本原理
-
- 简化约束条件
- 对偶问题(dual problem)
- 软间隔与松弛变量
- 核函数
- 数学方法
-
- 拉格朗日对偶转化
- SMO算法(Sequential Minimal Optimization)
- SVM实现
-
- 简单线性SVM
-
- 可视化训练集
- SMO算法
- 附数据集
- sklearn实现线性SVM
- 可视化比较线性核与高斯核
简介
支持向量机(support vector machines,SVM)是一种二分类模型,分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面。但是能将训练样本分开的划分超平面可能有很多,我们的目的就是找到两类训练样本“正中间”的划分超平面。其学习策略是使间隔最大化,最终转换为一个凸二次规划问题的求解。
概念解释
对于普通的SVM分类器,是借助超平面进行分类,故只适用于线性可分的情况。
- 线性可分性(linear separability)
给定一个数据集,如果存在超平面能将正实例点和负实例完全划分到超平面的两侧,则为线性可分;否则线性不可分。
线性可分模型举例:
线性不可分模型举例:
- 超平面(hyper plane)
超平面是由三维空间中的平面向高维推广的概念,其本质是自由度比空间维度小1的“平面”。自由度可以理解为超平面方程的自由变量,例如三维空间中,对于平面 A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0(A、B、C、D已知),当x、y确定时z唯一确定,即x、y为自由变量,自由度为2。
在样本空间中,超平面用如下线性方程来表示: w T x + b = 0 w^Tx+b=0 wTx+b=0其中 ω \omega ω是超平面的法向量, b b b为位移项。
直观理解,这个超平面应该是最适合分开两类数据的“平面”。而一种判断最合适的方法是使超平面两侧的数据到超平面的距离最大,即所谓的“间隔”最大。
- 间隔
对于二分类任务的SVM,将类别即为 { − 1 , 1 } \{-1,1\} {−1,1}。学习目标是得到超平面 w T + b = 0 w^T+b=0 wT+b=0将所有训练数据(线性可分时)分割到其两侧。显然 ∣ w T + b ∣ |w^T+b| ∣wT+b∣可以用于衡量数据点到超平面的距离。如果规定当 w T + b > 0 w^T+b>0 wT+b>0时 y y y的类别为正,即取值为1,则对于任意的数据,我们可以用 w T + b w^T+b wT+b的符号来衡量数据点在超平面的哪一侧,同时通过判断与 y y y符号同或异来判断分类是否正确。即可以用 y ∗ ( w T + b ) y*(w^T+b) y∗(wT+b)的正负性表示数据的分类正确与否。
由此引出函数间隔: γ ^ = y ∗ ( w T + b ) \hat \gamma=y*(w^T+b) γ^=y∗(wT+b)。
但是用函数间隔去训练超平面有一个问题。在训练参数时,如果 w w w和 b b b等比例变化,会引起函数间隔的变化,但此时超平面保持不变。也就是说会产生“无效”的训练。
于是我们找到一种消除等比例变化的方法,即几何间隔:
γ ^ = y ∗ ( w T x + b ) ∣ ∣ w ∣ ∣ \hat \gamma=\frac{y*(w^Tx+b)}{||w||} γ^=∣∣w∣∣y∗(wTx+b)
其中 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣是 w w w的L2范数(即欧式距离),当 w → k w , b → k b w\rightarrow kw,b\rightarrow kb w→kw,b→kb时, ∣ ∣ w ∣ ∣ → k ∣ ∣ w ∣ ∣ ||w||\rightarrow k||w|| ∣∣w∣∣→k∣∣w∣∣。
对一个数据点进行分类,当超平面离数据点的“间隔”越大,分类的**置信度(confidence)**也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化几何间隔。最优的超平面就是最大几何间隔超平面。
故学习任务为 γ ^ = m a x γ ^ i \hat\gamma=max\ \hat\gamma_i γ^=max γ^i。
- 支持向量
样本空间中距离超平面最近的一个或多个点。如上图中的实心红点和空心红点。
基本原理
简化约束条件
最优化方法解决的是如何求出最优超平面的问题。
首先我们需要找到两类支持向量并求出几何间隔,相加后使间距和最大。取 r = m i n r i r=min\ r_i r=min ri,所以支持向量到超平面的距离为r,其他点到超平面的距离大于r。
这里有几个最小最大不好理解。用一句话说就是先确定超平面,找最小间隔对应的点,然后只考虑这个点(一个或多个),不断学习w、b。当然每次更新参数后需要重新计算支持向量。
于是有:
y ∗ ( w T + b ) ∣ ∣ w ∣ ∣ ≥ r \frac{y*(w^T+b)}{||w||} \geq r ∣∣w∣∣y∗(wT+b)≥r
令 ∣ ∣ w ∣ ∣ ∗ r = 1 ||w||*r=1 ∣∣w∣∣∗r=1,有
y ∗ ( w T + b ) ≥ 1 y*(w^T+b)\geq 1 y∗(wT+b)≥1
这里是因为w和b可以等比例扩大而超平面不变,无论r是多少,我们都可以对w和b进行相应的变换,使 ∣ ∣ w ∣ ∣ ∗ r = 1 ||w||*r=1 ∣∣w∣∣∗r=1。即 r = 1 ∣ ∣ w ∣ ∣ r=\frac 1{||w||} r=∣∣w∣∣1。
要使异类支持向量到超平面的距离和最大,即
m a x w , b 2 ∣ ∣ w ∣ ∣ s . t . y i ( w T x i + b ) ≥ 1 max_{w,b}\ \frac 2{||w||}\ \ \ \ s.t.\ y_i(w^Tx_i+b) \geq 1 maxw,b ∣∣w∣∣2 s.t. yi(wTxi+b)≥1
s . t . s.t. s.t.即subject to,受限制于······
稍微变化一下,约束条件就是 m i n w , b 1 2 ∣ ∣ w ∣ ∣ 2 min_{w,b}\ \frac 12||w||^2 minw,b 21∣∣w∣∣2(平方是为了消掉根号)。
以上是支持向量机的基本型。
对偶问题(dual problem)
目标函数为二次,约束条件是线性的的问题称为凸二次规划问题。可以用现成的QP(Quadratic Programming,二次规划)优化包求解。
这里使用另一种方法,即将原问题通过引入拉格朗日乘子,变换到更容易求解的等价的对偶问题。
**拉格朗日对偶性(Lagrange Duality)**基本思想:引入拉格朗日乘子 α \alpha α,将含有n个变量k个约束条件的约束优化问题转换为含有n+k个变量的无约束优化问题,即把条件极值转换为无条件极值。
所以,我们把上面的优化问题转换成其对偶问题。定义拉格朗日函数:
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 − Σ i = 1 n α i [ y i ( w T x i + b ) − 1 ] L(w,b,\alpha)=\frac12||w||^2-\Sigma_{i=1}^n\alpha_i[y_i(w^Tx_i+b)-1] L(w,b,α)=21∣∣w∣∣2−Σi=1nαi[yi(wTxi+b)−1]
然后令 θ ( w ) = m a x a i ≥ 0 L ( w , b , α ) \theta(w)=max_{a_i\geq 0}L(w,b,\alpha) θ(w)=maxai≥0L(w,b,α),原问题即为 m i n w , b θ ( w ) min_{w,b}\theta(w) minw,bθ(w)。
由之前的数学推导,可以将原问题转化为对偶问题 m a x α i ≥ 0 m i n w , b L ( w , b , α ) = d ∗ max_{\alpha_i\geq0}min_{w,b}L(w,b,\alpha)=d^* maxαi≥0minw,bL(w,b,α)=d∗,这里 d ∗ d^* d∗是 p ∗ p^* p∗的近似解,二者满足 d ∗ ≤ p ∗ d^*\leq p^* d∗≤p∗,且在满足KKT条件时两者等价。
求解此对偶问题,可以划分为两步:
- m i n w 、 b min_{w、b} minw、b;
- 求解 α \alpha α(这一步使用SMO算法);
- 第一步
分别对w、b求偏导:
∂ L ∂ w = 0 ⇒ w = Σ i = 1 n α i y i x i \frac{\partial L}{\partial w}=0\Rightarrow w=\Sigma_{i=1}^n\alpha_iy_ix_i ∂w∂L=0⇒w=Σi=1nαiyixi
∂ L ∂ b = 0 ⇒ Σ i = 1 n α i y i = 0 \frac{\partial L}{\partial b}=0\Rightarrow \Sigma_{i=1}^n\alpha_iy_i=0 ∂b∂L=0⇒Σi=1nαiyi=0
将对w求偏导的式子带回函数 L ( w , b , α ) L(w,b,\alpha) L(w,b,α)中:
![]()
由此消去了 w , b w,b w,b(只是消去,并没有求出),将拉格朗日方程转换为只包含一个变量即 α \alpha α的形式。将对偶问题转换为:
m a x α Σ i = 1 n α i − 1 2 Σ i , j = 1 n α i α j y i y j x i T x j s . t . , α i ≥ 0 , i = 1 , . . . , n Σ i = 1 n α i y i = 0 max_{\alpha}\Sigma_{i=1}^n\alpha_i-\frac12\Sigma_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_i^Tx_j\\s.t.,\alpha_i\geq0,i=1,...,n \\\ \ \ \ \ \ \ \ \ \Sigma_{i=1}^n\alpha_iy_i=0 maxαΣi=1nαi−21Σi,j=1nαiαjyiyjxiTxjs.t.,αi≥0,i=1,...,n Σi=1nαiyi=0
- 第二步:SMO算法(Sequential Minimal Optimization,序列最小优化算法)
基本思路:每次选出两个分量 α i , α j \alpha_i,\alpha_j αi,αj进行调整,其他分量保持不变,在得到解后,再用其改变其他分量。
注意到当 α \alpha α不满足KTT条件时,目标函数会在迭代后减小(前面提到了对偶问题的解更小)。于是SMO采用了一个启发式:先选取一个违背KTT条件最大的变量,再选取另一个阈值间隔最大的变量,然后再更新变量。
在只考虑 α i \alpha_i αi和 α j \alpha_j αj时,将第一步推导出的约束条件重写成
α i y i + α j y j = c , α i , j ≥ 0 \alpha_iy_i+\alpha_jy_j=c,\alpha_{i,j}\geq0 αiyi+αjyj=c,αi,j≥0
其中, c = − Σ k ≠ i , j α k y k c=-\Sigma_{k\neq i,j}\alpha_ky_k c=−Σk=i,jαkyk。
也就是将 Σ i = 1 n α i y i = 0 \Sigma_{i=1}^n\alpha_iy_i=0 Σi=1nαiyi=0中的两项提出来,其余看成常数
于是可以消去约束问题中的 α j \alpha_j αj(用 α i \alpha_i αi的式子带入),转换为单变量的二次规划问题,从而求出 α i \alpha_i αi。
详情见数学方法部分。
软间隔与松弛变量
在线性不可分的一些问题里,有时候将数据映射到高维空间后,仍然不好处理,或是数据本身有噪点。这时为了避免过拟合,我们引入松弛变量,允许SVM在一些样本上出错,将约束条件变为:
y i ( w T x i + b ) ≥ 1 − ξ i ξ i ≥ 0 , i = 1 , 2 , . . . , m y_i(w^Tx_i+b)\geq 1-\xi_i\\\xi_i\geq0,i=1,2,...,m yi(wTxi+b)≥1−ξiξi≥0,i=1,2,...,m
其中 ξ i ≥ 0 \xi_i\geq 0 ξi≥0称为松弛变量,当然此时目标函数也要相应改变:
m i n w , b , ξ i 1 2 ∣ ∣ w ∣ ∣ 2 + C Σ i = 1 m ξ i min_{w,b,\xi_i}\frac12||w||^2+C\Sigma_{i=1}^m\xi_i minw,b,ξi21∣∣w∣∣2+CΣi=1mξi
后续步骤与之前做硬间隔处理时类似。
此时 0 ≤ α i ≤ C 0\leq\alpha_i\leq C 0≤αi≤C,不同样本点且对应的位置为:
α i = 0 ⇒ y i f ( x i ) ≥ 1 α_i=0⇒y_if(x_i)≥1 αi=0⇒yif(xi)≥1
0 < α i < C ⇒ y i f ( x i ) = 1 0<α_i
α i = C ⇒ y i f ( x i ) ≤ 1 α_i=C⇒y_if(x_i)≤1 αi=C⇒yif(xi)≤1
核函数
上述讨论均建立在训练样本线性可分的条件上。当问题不是线性可分的的时候,通过引入核函数 κ ( ⋅ , ⋅ ) \kappa(·,·) κ(⋅,⋅)可以将样本空间映射到一个更高维的特征空间,并使样本在该空间内线性可分。
在线性不可分的情况下,SVM首先在低位空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面。
例如,对于上面二维的线性不可分问题,一个明显的分界应该是一个圆圈,二不能用直线(二维中的超平面)划分,用于分界的圆圈在二维空间中可以表示为:
a 1 X 1 + a 2 X 2 + a 3 X 1 X 2 + a 4 X 1 2 + a 5 X 2 2 + a 6 = 0 a_1X_1+a_2X_2+a_3X_1X_2+a_4X_1^2+a_5X_2^2+a_6=0 a1X1+a2X2+a3X1X2+a4X12+a5X22+a6=0
通过 Z 1 = X 1 X 2 , Z 2 = X 1 2 , Z 3 = X 2 2 , Z 4 = X 1 , Z 5 = X 2 Z_1=X_1X_2,Z_2=X_1^2,Z_3=X_2^2,Z_4=X_1,Z_5=X_2 Z1=X1X2,Z2=X12,Z3=X22,Z4=X1,Z5=X2变换,将二维投射到五维空间,就可以将问题转换为线性问题。
相当于把问题:
![]()
中的 x i − > ϕ ( x i ) , x j − > ϕ ( x j ) x_i->\phi(x_i), x_j->\phi(x_j) xi−>ϕ(xi),xj−>ϕ(xj),将目标函数重写成:
m a x α α i − 1 2 Σ i , j = 1 n α i α j y i y j κ ( x i , x j ) max_\alpha \alpha_i-\frac12\Sigma_{i,j=1}^n\alpha_i\alpha_jy_iy_j\kappa(x_i,x_j) maxααi−21Σi,j=1nαiαjyiyjκ(xi,xj)
这个方法虽然简便,但是低维到高维的数目是爆炸增长的。二维映射到五维,三维映射到十九维,等等,这在计算时是难以接受的。
我们比较上面提到的二维问题中映射后的内积 < ϕ ( x 1 ) , ϕ ( x 2 ) > <\phi(x_1),\phi(x_2)> <ϕ(x1),ϕ(x2)>和 ( < x 1 , x 2 > + 1 ) 2 (
这种将两个向量隐式映射到高维空间中的函数叫核函数。用这种方法就可以将分类函数和对偶问题中的内积隐式映射到高维,而避免在高维中的计算。
我们引入核函数通常是希望将样本空间映射到线性可分的特征空间中,然而在不知道特征映射的形式时,我们不知道什么样的核函数是合适的。于是核函数的选择是SVM中的最大变数,很大程度上决定了SVM的性能。
列举几个常用的核函数。
| 名称 | 表达式 | 参数 |
|---|---|---|
| 线性核 | κ ( x i , x j ) = x i T x j \kappa(x_i,x_j)=x_i^Tx_j κ(xi,xj)=xiTxj | |
| 多项式核 | κ ( x i , x j ) = ( x i T x j ) d \kappa(x_i,x_j)=(x^T_ix_j)^d κ(xi,xj)=(xiTxj)d | d ≥ 1 d\geq1 d≥1为多项式的次数 |
| 高斯核 | κ ( x i , x j ) = \kappa(x_i,x_j)= κ(xi,xj)= e x p ( − ∥ x i − x j ∥ 2 σ 2 ) exp(- \frac{\|x_i-x_j\|^2}{\sigma^2}) exp(−σ2∥xi−xj∥2) |
σ > 0 \sigma>0 σ>0为高斯核的带宽 |
| 拉普拉斯核 | κ ( x i , x j ) = \kappa(x_i,x_j)= κ(xi,xj)= e x p ( − ∥ x i − x j ∥ σ ) exp(-\frac{\|x_i-x_j\|}{\sigma}) exp(−σ∥xi−xj∥) |
σ > 0 \sigma>0 σ>0 |
| Sigmoid核 | κ ( x i , x j ) = t a n h ( β x i T x j + θ ) \kappa(x_i,x_j)=tanh(\beta x_i^Tx_j+\theta) κ(xi,xj)=tanh(βxiTxj+θ) | β > 0 , θ < 0 \beta>0,\theta<0 β>0,θ<0 |
数学方法
拉格朗日对偶转化
转换对偶问题一般有两步:
- 将有约束的目标函数转换为无约束的拉格朗日函数
- 使用拉格朗日对称性,将不易求解的问题转换为易求解的问题
- 第一步:
由于我们要求解的是最小化问题,有一种方法是构造一个函数,使该函数在可行区域内与原目标函数完全一致,而在可行解区域外的数值无穷大。
拉格朗日乘数法
对于目标函数 f ( x ) f(x) f(x)和约束条件 g i ( x ) ≤ 0 , i = 1 , 2 , . . . , m g_i(x)\leq0,\ i=1,2,...,m gi(x)≤0, i=1,2,...,m和 h j ( x ) = 0 , j = 1 , 2 , . . . , k h_j(x)=0,\ j=1,2,...,k hj(x)=0, j=1,2,...,k,构成约束问题:
m i n f ( x ) s . t . g i ( x ) ≤ 0 ; h j ( x ) = 0 , i = 1 , 2 , . . . , m , j = 1 , 2 , . . . , k min\ f(x)\ s.t.\ g_i(x)\leq0;h_j(x)=0,\ i=1,2,...,m,\ j=1,2,...,k min f(x) s.t. gi(x)≤0;hj(x)=0, i=1,2,...,m, j=1,2,...,k
引入拉格朗日乘子 α \alpha α,构造拉格朗日函数:
L ( x , α , β ) = f ( x ) + Σ i = 1 m α i g i ( x ) + Σ j = 1 k β j h j ( x ) , i = 1 , 2 , . . . , m , j = 1 , 2 , . . . , k L(x,\alpha,\beta)=f(x)+\Sigma_{i=1}^m\alpha_ig_i(x)+\Sigma_{j=1}^k\beta_jh_j(x),\ i=1,2,...,m,\ j=1,2,...,k L(x,α,β)=f(x)+Σi=1mαigi(x)+Σj=1kβjhj(x), i=1,2,...,m, j=1,2,...,k
导出方程组:
{ ∂ L ∂ x i = ∂ f ∂ x i + α i ∂ g i ∂ x i = 0 ,i=1,2,...,m ∂ L ∂ x j = ∂ f ∂ x j + β j ∂ h j ∂ x j = 0 j=1,2,...,k ∂ L ∂ α i = g i = 0 ,i=1,2,...,m ∂ L ∂ α j = h j = 0 ,j=1,2,...,k \begin{cases}\frac{\partial L}{\partial x_i}=\frac{\partial f}{\partial x_i}+\alpha_i\frac{\partial g_i}{\partial x_i}=0&\text{,i=1,2,...,m}\\\frac{\partial L}{\partial x_j}=\frac{\partial f}{\partial x_j}+\beta_j\frac{\partial h_j}{\partial x_j}=0&\text{j=1,2,...,k}\\\frac{\partial L}{\partial \alpha_i}=g_i=0&\text{,i=1,2,...,m}\\\frac{\partial L}{\partial \alpha_j}=h_j=0&\text{,j=1,2,...,k}\end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧∂xi∂L=∂xi∂f+αi∂xi∂gi=0∂xj∂L=∂xj∂f+βj∂xj∂hj=0∂αi∂L=gi=0∂αj∂L=hj=0,i=1,2,...,mj=1,2,...,k,i=1,2,...,m,j=1,2,...,k
对应的解 x ‾ = ( x ‾ 1 , x ‾ 2 , . . . , x ‾ n ) \overline x=(\overline x_1,\overline x_2,...,\overline x_n) x=(x1,x2,...,xn)即为目标函数在约束条件下的极小值点。
然而,拉格朗日数乘法使用求导的方法求解依然困难,这里使用一个数学技巧,即
拉格朗日对偶
构造关于 x x x的函数:
θ p ( x ) = m a x α , β ; α i ≥ 0 L ( x , α , β ) \theta_p(x)=max_{\alpha,\beta;\alpha_i\geq0}L(x,\alpha,\beta) θp(x)=maxα,β;αi≥0L(x,α,β)
在 g ( x ) > 0 g(x)>0 g(x)>0或 h ( x ) ≠ 0 h(x)\neq0 h(x)=0时,令 α → ∞ \alpha\rightarrow\infty α→∞或 β → ∞ \beta\rightarrow\infty β→∞;否则 α = 0 , β = 0 \alpha=0,\beta=0 α=0,β=0,于是有
θ p ( x ) = { f ( x ) ,x满足约束条件 + ∞ ,其它 \theta_p(x)=\begin{cases}f(x)&\text{,x满足约束条件}\\+\infty&\text{,其它}\end{cases} θp(x)={f(x)+∞,x满足约束条件,其它
至此我们将极小化问题转换为
m i n x m a x α , β ; α i ≥ 0 L ( x , α , β ) min_xmax_{\alpha,\beta;\alpha_i\geq0}L(x,\alpha,\beta) minxmaxα,β;αi≥0L(x,α,β)
定义原问题的最优值 p ∗ = m i n x θ p ( α , β ) p^*=min_x\ \theta_p(\alpha,\beta) p∗=minx θp(α,β)
- 第二步:
转换为拉格朗日对偶问题
上述极小极大问题的对偶问题为极大极小问题:
m a x α , β ; α i ≥ 0 m i n x L ( x , α , β ) max_{\alpha,\beta;\alpha_i\geq0}min_xL(x,\alpha,\beta) maxα,β;αi≥0minxL(x,α,β)
则对偶问题的最优值 d ∗ = m a x α , β ; α i ≥ 0 θ p ( α , β ) d^*=max_{\alpha,\beta;\alpha_i\geq0}\ \theta_p(\alpha,\beta) d∗=maxα,β;αi≥0 θp(α,β)
- 原始问题与对偶问题的关系
为什么要对偶处理?
对于原问题,
只要原问题和对偶问题都有最优解,即满足弱对偶性: d ∗ ≥ p ∗ d^*\geq p^* d∗≥p∗
而如果我们找到取等的条件(即满足强对偶性: d ∗ = p ∗ d^*=p^* d∗=p∗),使二者的最优解相等,就可以通过求解对偶问题来求解原问题。使强对偶性成立的条件有很多,比如Slater条件和KKT条件。这里不加证明地使用KKT条件。
- KKT(Karush-Kuhn-Tucker)条件
∇ x L ( x ∗ , α ∗ , β ∗ ) = 0 \nabla_xL(x^*,\alpha^*,\beta^*)=0 ∇xL(x∗,α∗,β∗)=0
g i ( x ) ≤ 0 g_i(x)\leq0 gi(x)≤0
h j ( x ) = 0 h_j(x)=0 hj(x)=0
α i ≥ 0 \alpha_i\geq0 αi≥0
α i g i ( x ) = 0 \alpha_ig_i(x)=0 αigi(x)=0
SMO算法(Sequential Minimal Optimization)
- 坐标上升法(Coordinate Ascent)
SMO算法的思想与坐标上升算法的思想类似,所以在此通过坐标上升法来引入SMO算法。
坐标上升法,即每次通过更新多元函数中的一维,多次迭代直到收敛来达到优化函数的目的。
例如,对于优化问题 m a x α W ( α 1 , α 2 , . . . , α n ) max_\alpha W(\alpha_1,\alpha2,...,\alpha_n) maxαW(α1,α2,...,αn),我们每次选取一个 α i \alpha_i αi,通过更新 α i \alpha_i αi使其向极大值靠近,多次重复,直到函数达到局部最优。
因为每次只是做一维优化,所以每个循环中的优化过程的效率是很高的, 但是迭代的次数会比较多。
- SMO算法介绍
先给出SVM问题的对偶形式:
m a x α Σ i = 1 n α i − 1 2 Σ i , j = 1 n α i α j y i y j x i T x j s . t . , α i ≥ 0 , i = 1 , . . . , n Σ i = 1 n α i y i = 0 max_{\alpha}\Sigma_{i=1}^n\alpha_i-\frac12\Sigma_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_i^Tx_j\\s.t.,\alpha_i\geq0,i=1,...,n \\\ \ \ \ \ \ \ \ \ \Sigma_{i=1}^n\alpha_iy_i=0 maxαΣi=1nαi−21Σi,j=1nαiαjyiyjxiTxjs.t.,αi≥0,i=1,...,n Σi=1nαiyi=0
不妨将目标函数写成:
m i n 1 2 Σ i = 1 , j = 1 n y i y j α i α j K i j − Σ i = 1 n α i min\frac12\Sigma_{i=1,j=1}^ny_iy_j\alpha_i\alpha_jK_{ij}-\Sigma_{i=1}^n\alpha_i min21Σi=1,j=1nyiyjαiαjKij−Σi=1nαi
其中 K i j = ( x i ⋅ x j ) K_{ij}=(x_i·x_j) Kij=(xi⋅xj)
在这个问题中,我们需要对 m a x α L ( α 1 , α 2 , . . . , α n ) max_\alpha L(\alpha_1,\alpha2,...,\alpha_n) maxαL(α1,α2,...,αn)进行优化。所以SMO算法每次选取一对变量 ( α i , α j ) , ( i ≠ j ) (\alpha_i,\alpha_j),(i\neq j) (αi,αj),(i=j),不妨令 i = 1 , j = 2 i=1,j=2 i=1,j=2。
注意这里不能像坐标上升法那样只选取一个 α \alpha α进行更新,因为这里的 α \alpha α具有约束 Σ i = 1 n α i y i = 0 \Sigma_{i=1}^n\alpha_iy_i=0 Σi=1nαiyi=0,使得当更新一个 α i \alpha_i αi时,必然需要更新另一个 α j \alpha_j αj使得约束条件成立。
硬间隔下的最优
记 v i = Σ j = 3 n y j α j K i j v_i=\Sigma_{j=3}^ny_j\alpha_jK_{ij} vi=Σj=3nyjαjKij逐步化简目标函数:,将含有 α 1 、 α 2 \alpha_1、\alpha_2 α1、α2的式子提出
m i n 1 2 Σ i = 1 , j = 1 n y i y j α i α j K i j − Σ i = 1 n α i = m i n 1 2 Σ i , j = 3 n y i y j α i α j K i j − Σ i = 3 n α i − ( α 1 + α 2 ) + 1 2 ( α 1 2 K 11 + α 2 2 K 22 + 2 α 1 α 2 y 1 y 2 K 12 + 2 α 1 y 1 v 1 + 2 α 2 y 2 v 2 ) min\frac12\Sigma_{i=1,j=1}^ny_iy_j\alpha_i\alpha_jK_{ij}-\Sigma_{i=1}^n\alpha_i\\=min\frac12\Sigma_{i,j=3}^ny_iy_j\alpha_i\alpha_jK_{ij}-\Sigma_{i=3}^n\alpha_i-(\alpha_1+\alpha_2)+\frac12(\alpha_1^2K_{11}+\alpha_2^2K_{22}+2\alpha_1\alpha_2y_1y_2K_{12}+2\alpha_1y_1v_1+2\alpha_2y_2v_2) min21Σi=1,j=1nyiyjαiαjKij−Σi=1nαi=min21Σi,j=3nyiyjαiαjKij−Σi=3nαi−(α1+α2)+21(α12K11+α22K22+2α1α2y1y2K12+2α1y1v1+2α2y2v2)
且 α 1 、 α 2 \alpha_1、\alpha_2 α1、α2有关系:
α 1 y 1 + α 2 y 2 = − Σ i ≠ 1 , 2 n α i y i = C \alpha_1y_1+\alpha_2y_2=-\Sigma_{i\neq1,2}^n \alpha_iy_i= C α1y1+α2y2=−Σi=1,2nαiyi=C
两边同时乘以 y 1 y_1 y1,得
α 1 = C y 1 − α 2 y 2 y 1 α 1 2 = ( k − α 2 y 2 ) 2 = C 2 − 2 C α 2 y 2 + α 2 2 2 y 1 y 2 α 1 α 2 K 12 = 2 ( C y 2 − α 2 ) α 2 K 12 2 y 1 α 1 v 1 = 2 ( ξ i − α 2 y 2 ) v 1 \alpha_1=Cy_1-\alpha_2y_2y_1\\\alpha_1^2=(k-\alpha_2y_2)^2=C^2-2C\alpha_2y_2+\alpha_2^2\\2y_1y_2\alpha_1\alpha_2K_{12}=2(Cy_2-\alpha_2)\alpha_2K_{12}\\2y_1\alpha_1v_1=2(\xi_i-\alpha_2y_2)v_1 α1=Cy1−α2y2y1α12=(k−α2y2)2=C2−2Cα2y2+α222y1y2α1α2K12=2(Cy2−α2)α2K122y1α1v1=2(ξi−α2y2)v1
带入到目标函数中,化简得
m i n α 2 1 2 ( K 11 + K 22 − 2 K 12 ) α 2 2 + ( y 1 y 2 − 1 − C y 2 K 11 + C y 2 K 12 − y 2 v 1 + y 2 v 2 ) α 2 + 1 2 C 2 K 11 + C v 1 − C y 1 min_{\alpha_2}\frac12(K_{11}+K_{22}-2K_{12})\alpha_2^2+(y_1y_2-1-Cy_2K_{11}+Cy_2K_{12}-y_2v_1+y_2v_2)\alpha_2+\frac12C^2K_{11}+Cv_1-Cy_1 minα221(K11+K22−2K12)α22+(y1y2−1−Cy2K11+Cy2K12−y2v1+y2v2)α2+21C2K11+Cv1−Cy1
记为 m i n α 2 W ( α 2 ) min_{\alpha_2}W(\alpha_2) minα2W(α2),凸函数在 ∂ W ∂ α 2 = 0 \frac{\partial W}{\partial\alpha_2}=0 ∂α2∂W=0处取极值
∂ W ∂ α 2 = ( K 11 + K 22 − 2 K 12 ) α 2 + ( y 1 y 2 − 1 − C y 2 K 11 + C y 2 K 12 − y 2 v 1 + y 2 v 2 ) = 0 \frac{\partial W}{\partial\alpha_2}=(K_{11}+K_{22}-2K_{12})\alpha_2+(y_1y_2-1-Cy_2K_{11}+Cy_2K_{12}-y_2v_1+y_2v_2)=0 ∂α2∂W=(K11+K22−2K12)α2+(y1y2−1−Cy2K11+Cy2K12−y2v1+y2v2)=0
故可以解出 α 2 \alpha_2 α2我们将一开始取定的 α 1 α 2 \alpha_1\alpha_2 α1α2记为 α 1 o l d α 2 o l d \alpha_1^{old}\alpha_2^{old} α1oldα2old,解出的 α 1 α 2 \alpha_1\alpha_2 α1α2记为 α 1 n e w α 2 n e w \alpha_1^{new}\alpha_2^{new} α1newα2new。
K 11 + K 22 − 2 K 12 = ( x 1 + x 2 ) 2 K_{11}+K_{22}-2K_{12}=(x_1+x_2)^2 K11+K22−2K12=(x1+x2)2,记为 κ \kappa κ。
同时记 f ( x i ) = Σ j = 1 n y j α j K i j f(x_i)=\Sigma_{j=1}^ny_j\alpha_jK_{ij} f(xi)=Σj=1nyjαjKij(即超平面方程),则 v 1 、 v 2 v_1、v_2 v1、v2用 g ( x 1 ) 、 g ( x 2 ) g(x_1)、g(x_2) g(x1)、g(x2)表示为
v 1 = g ( x 1 ) + y 2 α 2 ( K 11 − K 12 − C K 11 ) v_1=g(x_1)+y_2\alpha_2(K_{11}-K_{12}-CK_{11}) v1=g(x1)+y2α2(K11−K12−CK11)
v 2 = g ( x 2 ) + y 2 α 2 ( K 21 − K 22 − C K 21 ) v_2=g(x_2)+y_2\alpha_2(K_{21}-K_{22}-CK_{21}) v2=g(x2)+y2α2(K21−K22−CK21)
v 1 − v 2 = f ( x 1 ) − f ( x 2 ) + y 2 κ α 2 − C ( K 11 − K 12 ) v_1-v_2=f(x_1)-f(x_2)+y_2\kappa\alpha_2-C(K_{11}-K_{12}) v1−v2=f(x1)−f(x2)+y2κα2−C(K11−K12)
可以解出
y 2 κ α 2 n e w = − y 1 + y 2 + C K 11 − C K 12 + v 1 − v 2 = ( f ( x 1 ) − y 1 ) − ( f ( x 2 − y 2 ) ) + y 2 κ α 2 o l d y_2\kappa\alpha_2^{new}=-y_1+y_2+CK_{11}-CK_{12}+v_1-v_2\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ =(f(x_1)-y_1)-(f(x_2-y_2))+y_2\kappa\alpha_2^{old} y2κα2new=−y1+y2+CK11−CK12+v1−v2 =(f(x1)−y1)−(f(x2−y2))+y2κα2old
于是 α 2 n e w = α 2 o l d + y 2 ( E 1 − E 2 ) κ \alpha_2^{new}=\alpha_2^{old}+\frac{y_2(E_1-E_2)}{\kappa} α2new=α2old+κy2(E1−E2)
换成一般的下标,即为 α j n e w = α j o l d + y j ( E i − E j ) κ \alpha_j^{new}=\alpha_j^{old}+\frac{y_j(E_i-E_j)}{\kappa} αjnew=αjold+κyj(Ei−Ej)
我们先不着急算出 α i \alpha_i αi,在实际应用中我们常常要允许SVM”出错“,这时需要引入软间隔,此时约束条件也会相应改变。
软间隔下的最优
先分析一下软间隔时约束条件
0 ≤ α i ≤ C , i = 1 , . . . , n α 1 y 1 + α 2 y 2 = ξ 0\leq\alpha_i\leq C,i=1,...,n\\\alpha_1y_1+\alpha_2y_2=\xi 0≤αi≤C,i=1,...,nα1y1+α2y2=ξ
当取定 α 1 α 2 \alpha_1\alpha_2 α1α2时,四种情况下约束条件可以看做四条围成方形的直线
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0mgObYns-1589534426589)(https://pic3.zhimg.com/80/v2-449670775bab3c385b5e5930fc6d2caa_720w.png)]
此图中纵轴为 α 2 \alpha_2 α2,横轴为 α 1 \alpha_1 α1, k = ± ξ k=\pm\xi k=±ξ
左图解析式: α 2 = α 1 − k \alpha_2=\alpha_1-k α2=α1−k
右图解析式: α 2 = − α 1 + k \alpha_2=-\alpha_1+k α2=−α1+k
先分别求出上下界,从而确定 α n e w \alpha^{new} αnew的更新。
左图:
红线: m a x = C , m i n = − k max=C,min=-k max=C,min=−k,黑线: m a x = C − k , m i n = 0 max=C-k,min=0 max=C−k,min=0。
上界: H = m i n ( C , C − k ) = m i n ( C , C − α 1 o l d + α 2 o l d ) H=min(C,C-k)=min(C,C-\alpha_1^{old}+\alpha_2^{old}) H=min(C,C−k)=min(C,C−α1old+α2old)
下界: L = m a x ( 0 , − k ) = m a x ( 0 , α 2 o l d − α 1 o l d ) L=max(0,-k)=max(0,\alpha_2^{old}-\alpha_1^{old}) L=max(0,−k)=max(0,α2old−α1old)
右图:
红线: m a x = C , m i n = − C + k max=C,min=-C+k max=C,min=−C+k,黑线: m a x = k , m i n = 0 max=k,min=0 max=k,min=0
上界: H = m i n ( C , k ) = m i n ( C , α 1 o l d + α 2 o l d ) H=min(C,k)=min(C,\alpha_1^{old}+\alpha_2^{old}) H=min(C,k)=min(C,α1old+α2old)
下界: L = m a x ( 0 , − C + k ) = m i n ( 0 , − C + α 1 o l d + α 2 o l d ) L=max(0,-C+k)=min(0,-C+\alpha_1^{old}+\alpha_2^{old}) L=max(0,−C+k)=min(0,−C+α1old+α2old)
求出上下界后,我们可以得到软间隔下的 α 2 n e w \alpha_2^{new} α2new
α 2 n e w = { H α 2 n e w > H α 2 n e w L ≤ α 2 n e w ≤ H L α 2 n e w < L \alpha_2^{new}=\begin{cases}H&\alpha_2^{new}>H\\\alpha_2^{new}&L\leq\alpha_2^{new}\leq H\\L&\alpha_2^{new}
其中右式中的 α 2 n e w \alpha_2^{new} α2new为硬间隔下的更新值,左式为软间隔下的更新值。
求出 α 2 n e w \alpha_2^{new} α2new后,根据 α 1 o l d + α 2 o l d = α 1 n e w + α 2 n e w \alpha_1^{old}+\alpha_2^{old}=\alpha_1^{new}+\alpha_2^{new} α1old+α2old=α1new+α2new,即可求出 α 1 n e w \alpha_1^{new} α1new。
更新 b b b
在对偶问题中,我们并没有用到 b b b,那为什么还需要更新 b b b呢?
m a x α Σ i = 1 n α i − 1 2 Σ i , j = 1 n α i α j y i y j x i T x j s . t . , α i ≥ 0 , i = 1 , . . . , n Σ i = 1 n α i y i = 0 max_{\alpha}\Sigma_{i=1}^n\alpha_i-\frac12\Sigma_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_i^Tx_j\\s.t.,\alpha_i\geq0,i=1,...,n \\\ \ \ \ \ \ \ \ \ \Sigma_{i=1}^n\alpha_iy_i=0 maxαΣi=1nαi−21Σi,j=1nαiαjyiyjxiTxjs.t.,αi≥0,i=1,...,n Σi=1nαiyi=0
我们发现,在 α \alpha α的更新过程中 α j n e w = α j o l d + y j ( E i − E j ) κ \alpha_j^{new}=\alpha_j^{old}+\frac{y_j(E_i-E_j)}{\kappa} αjnew=αjold+κyj(Ei−Ej), E E E的计算时用到了 b b b,所以 b b b的值也会影响到 α \alpha α的更新,故我们需要更新 b b b。
我们选取了两个支持向量,均满足 y i ( w T x + b ) = 1 ⇒ Σ j = 1 n α j y j K j i + b = y i y_i(w^Tx+b)=1\Rightarrow \Sigma_{j=1}^n\alpha_jy_jK_{ji}+b=y_i yi(wTx+b)=1⇒Σj=1nαjyjKji+b=yi。
可以更新 b b b:
b 1 n e w = − E 1 + ( α 1 o l d − α 1 n e w ) y 1 K 11 + ( α 2 o l d − α 2 n e w ) y 2 K 21 + b o l d b_1^{new}=-E1+(\alpha_1^{old}-\alpha_1^{new})y_1K_{11}+(\alpha_2^{old}-\alpha_2^{new})y_2K_{21}+b^{old} b1new=−E1+(α1old−α1new)y1K11+(α2old−α2new)y2K21+bold
b 2 n e w = − E 2 + ( α 1 o l d − α 1 n e w ) y 1 K 12 + ( α 2 o l d − α 2 n e w ) y 2 K 22 + b o l d b_2^{new}=-E2+(\alpha_1^{old}-\alpha_1^{new})y_1K_{12}+(\alpha_2^{old}-\alpha_2^{new})y_2K_{22}+b^{old} b2new=−E2+(α1old−α1new)y1K12+(α2old−α2new)y2K22+bold
最终选择二者均值作为新的 b b b
b n e w = b 1 n e w + b 2 n e w 2 b^{new}=\frac{b_1^{new}+b_2^{new}}{2} bnew=2b1new+b2new
SVM实现
简单线性SVM
代码来自Jack-Cherish/Machine-Learning
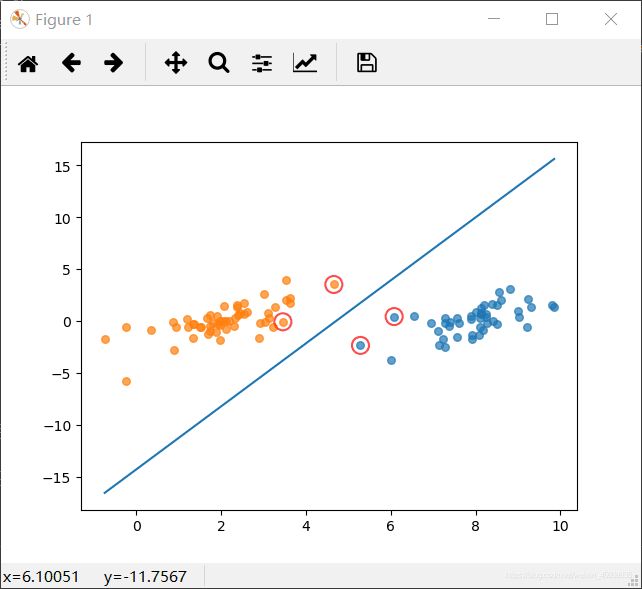
先上最后结果
可视化训练集
# -*- coding:UTF-8 -*-
import matplotlib.pyplot as plt
import numpy as np
"""
函数说明:读取数据
Parameters:
fileName - 文件名
Returns:
dataMat - 数据矩阵
labelMat - 数据标签
Author:
Jack Cui
Blog:
http://blog.csdn.net/c406495762
Zhihu:
https://www.zhihu.com/people/Jack--Cui/
Modify:
2017-09-21
"""
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines(): #逐行读取,滤除空格等
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(float(lineArr[2])) #添加标签
return dataMat,labelMat
"""
函数说明:数据可视化
Parameters:
dataMat - 数据矩阵
labelMat - 数据标签
Returns:
无
Author:
Jack Cui
Blog:
http://blog.csdn.net/c406495762
Zhihu:
https://www.zhihu.com/people/Jack--Cui/
Modify:
2017-09-21
"""
def showDataSet(dataMat, labelMat):
data_plus = [] #正样本
data_minus = [] #负样本
for i in range(len(dataMat)):
if labelMat[i] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus) #转换为numpy矩阵
data_minus_np = np.array(data_minus) #转换为numpy矩阵
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1]) #正样本散点图
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1]) #负样本散点图
plt.show()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet(r'D:\VS-Code-python\ML_algorithm\support_vector_machine\train_data.txt')
showDataSet(dataMat, labelMat)
SMO算法
# -*- coding:UTF-8 -*-
from time import sleep
import matplotlib.pyplot as plt
import numpy as np
import random
import types
"""
函数说明:读取数据
Parameters:
fileName - 文件名
Returns:
dataMat - 数据矩阵
labelMat - 数据标签
Author:
Jack Cui
Blog:
http://blog.csdn.net/c406495762
Zhihu:
https://www.zhihu.com/people/Jack--Cui/
Modify:
2017-09-21
"""
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines(): #逐行读取,滤除空格等
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(float(lineArr[2])) #添加标签
return dataMat,labelMat
"""
函数说明:随机选择alpha
Parameters:
i - alpha
m - alpha参数个数
Returns:
j -
Author:
Jack Cui
Blog:
http://blog.csdn.net/c406495762
Zhihu:
https://www.zhihu.com/people/Jack--Cui/
Modify:
2017-09-21
"""
def selectJrand(i, m):
j = i #选择一个不等于i的j
while (j == i):
j = int(random.uniform(0, m))
return j
"""
函数说明:修剪alpha
Parameters:
aj - alpha值
H - alpha上限
L - alpha下限
Returns:
aj - alpah值
Author:
Jack Cui
Blog:
http://blog.csdn.net/c406495762
Zhihu:
https://www.zhihu.com/people/Jack--Cui/
Modify:
2017-09-21
"""
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
"""
函数说明:简化版SMO算法
Parameters:
dataMatIn - 数据矩阵
classLabels - 数据标签
C - 松弛变量
toler - 容错率
maxIter - 最大迭代次数
Returns:
无
Author:
Jack Cui
Blog:
http://blog.csdn.net/c406495762
Zhihu:
https://www.zhihu.com/people/Jack--Cui/
Modify:
2017-09-23
"""
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
#转换为numpy的mat存储
dataMatrix = np.mat(dataMatIn); labelMat = np.mat(classLabels).transpose()
#初始化b参数,统计dataMatrix的维度
b = 0; m,n = np.shape(dataMatrix)
#初始化alpha参数,设为0
alphas = np.mat(np.zeros((m,1)))
#初始化迭代次数
iter_num = 0
#最多迭代matIter次
while (iter_num < maxIter):
alphaPairsChanged = 0
for i in range(m):
#步骤1:计算误差Ei
fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
Ei = fXi - float(labelMat[i])
#优化alpha,更设定一定的容错率。
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
#随机选择另一个与alpha_i成对优化的alpha_j
j = selectJrand(i,m)
#步骤1:计算误差Ej
fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
Ej = fXj - float(labelMat[j])
#保存更新前的aplpha值,使用深拷贝
alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
#步骤2:计算上下界L和H
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L==H: print("L==H"); continue
#步骤3:计算eta
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
if eta >= 0: print("eta>=0"); continue
#步骤4:更新alpha_j
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
#步骤5:修剪alpha_j
alphas[j] = clipAlpha(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001): print("alpha_j变化太小"); continue
#步骤6:更新alpha_i
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
#步骤7:更新b_1和b_2
b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
#步骤8:根据b_1和b_2更新b
if (0 < alphas[i]) and (C > alphas[i]): b = b1
elif (0 < alphas[j]) and (C > alphas[j]): b = b2
else: b = (b1 + b2)/2.0
#统计优化次数
alphaPairsChanged += 1
#打印统计信息
print("第%d次迭代 样本:%d, alpha优化次数:%d" % (iter_num,i,alphaPairsChanged))
#更新迭代次数
if (alphaPairsChanged == 0): iter_num += 1
else: iter_num = 0
print("迭代次数: %d" % iter_num)
return b,alphas
"""
函数说明:分类结果可视化
Parameters:
dataMat - 数据矩阵
w - 直线法向量
b - 直线解决
Returns:
无
Author:
Jack Cui
Blog:
http://blog.csdn.net/c406495762
Zhihu:
https://www.zhihu.com/people/Jack--Cui/
Modify:
2017-09-23
"""
def showClassifer(dataMat, w, b):
#绘制样本点
data_plus = [] #正样本
data_minus = [] #负样本
for i in range(len(dataMat)):
if labelMat[i] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus) #转换为numpy矩阵
data_minus_np = np.array(data_minus) #转换为numpy矩阵
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7) #正样本散点图
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7) #负样本散点图
#绘制直线
x1 = max(dataMat)[0]
x2 = min(dataMat)[0]
a1, a2 = w
b = float(b)
a1 = float(a1[0])
a2 = float(a2[0])
y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
plt.plot([x1, x2], [y1, y2])
#找出支持向量点
for i, alpha in enumerate(alphas):
if abs(alpha) > 0:
x, y = dataMat[i]
plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
plt.show()
"""
函数说明:计算w
Parameters:
dataMat - 数据矩阵
labelMat - 数据标签
alphas - alphas值
Returns:
无
Author:
Jack Cui
Blog:
http://blog.csdn.net/c406495762
Zhihu:
https://www.zhihu.com/people/Jack--Cui/
Modify:
2017-09-23
"""
def get_w(dataMat, labelMat, alphas):
alphas, dataMat, labelMat = np.array(alphas), np.array(dataMat), np.array(labelMat)
w = np.dot((np.tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)
return w.tolist()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet(r'D:\VS-Code-python\ML_algorithm\support_vector_machine\train_data.txt')
b,alphas = smoSimple(dataMat, labelMat, 0.6, 0.001, 40)
w = get_w(dataMat, labelMat, alphas)
showClassifer(dataMat, w, b)
附数据集
3.542485 1.977398 -1
3.018896 2.556416 -1
7.551510 -1.580030 1
2.114999 -0.004466 -1
8.127113 1.274372 1
7.108772 -0.986906 1
8.610639 2.046708 1
2.326297 0.265213 -1
3.634009 1.730537 -1
0.341367 -0.894998 -1
3.125951 0.293251 -1
2.123252 -0.783563 -1
0.887835 -2.797792 -1
7.139979 -2.329896 1
1.696414 -1.212496 -1
8.117032 0.623493 1
8.497162 -0.266649 1
4.658191 3.507396 -1
8.197181 1.545132 1
1.208047 0.213100 -1
1.928486 -0.321870 -1
2.175808 -0.014527 -1
7.886608 0.461755 1
3.223038 -0.552392 -1
3.628502 2.190585 -1
7.407860 -0.121961 1
7.286357 0.251077 1
2.301095 -0.533988 -1
-0.232542 -0.547690 -1
3.457096 -0.082216 -1
3.023938 -0.057392 -1
8.015003 0.885325 1
8.991748 0.923154 1
7.916831 -1.781735 1
7.616862 -0.217958 1
2.450939 0.744967 -1
7.270337 -2.507834 1
1.749721 -0.961902 -1
1.803111 -0.176349 -1
8.804461 3.044301 1
1.231257 -0.568573 -1
2.074915 1.410550 -1
-0.743036 -1.736103 -1
3.536555 3.964960 -1
8.410143 0.025606 1
7.382988 -0.478764 1
6.960661 -0.245353 1
8.234460 0.701868 1
8.168618 -0.903835 1
1.534187 -0.622492 -1
9.229518 2.066088 1
7.886242 0.191813 1
2.893743 -1.643468 -1
1.870457 -1.040420 -1
5.286862 -2.358286 1
6.080573 0.418886 1
2.544314 1.714165 -1
6.016004 -3.753712 1
0.926310 -0.564359 -1
0.870296 -0.109952 -1
2.369345 1.375695 -1
1.363782 -0.254082 -1
7.279460 -0.189572 1
1.896005 0.515080 -1
8.102154 -0.603875 1
2.529893 0.662657 -1
1.963874 -0.365233 -1
8.132048 0.785914 1
8.245938 0.372366 1
6.543888 0.433164 1
-0.236713 -5.766721 -1
8.112593 0.295839 1
9.803425 1.495167 1
1.497407 -0.552916 -1
1.336267 -1.632889 -1
9.205805 -0.586480 1
1.966279 -1.840439 -1
8.398012 1.584918 1
7.239953 -1.764292 1
7.556201 0.241185 1
9.015509 0.345019 1
8.266085 -0.230977 1
8.545620 2.788799 1
9.295969 1.346332 1
2.404234 0.570278 -1
2.037772 0.021919 -1
1.727631 -0.453143 -1
1.979395 -0.050773 -1
8.092288 -1.372433 1
1.667645 0.239204 -1
9.854303 1.365116 1
7.921057 -1.327587 1
8.500757 1.492372 1
1.339746 -0.291183 -1
3.107511 0.758367 -1
2.609525 0.902979 -1
3.263585 1.367898 -1
2.912122 -0.202359 -1
1.731786 0.589096 -1
2.387003 1.573131 -1
sklearn实现线性SVM
# -*- coding:utf-8 -*-
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import classification_report, confusion_matrix
if __name__ == '__main__':
#load data
filename = r'D:\VS-Code-python\ML_algorithm\support_vector_machine\bill_authentication.csv'
bankdata = pd.read_csv(filename)
#print(bankdata.head)
#properties
# Variance:图像的方差
# Skewness:偏度
# Kurtosis:峰度
# Entropy:熵
# Class:类别
#pretreatment
X = bankdata.drop('Class', axis=1)
y = bankdata['Class']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)
#training
svclassifier = SVC(kernel='linear')
svclassifier.fit(X_train, y_train)
#prediction
y_pred = svclassifier.predict(X_test)
#assessment
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))
- out:
[[151 1]
[ 0 123]]
precision recall f1-score support
0 1.00 0.99 1.00 152
1 0.99 1.00 1.00 123
micro avg 1.00 1.00 1.00 275
macro avg 1.00 1.00 1.00 275
weighted avg 1.00 1.00 1.00 275
可视化比较线性核与高斯核
# -*- coding:utf-8 -*-
import numpy as np
import pandas as pd
from sklearn import svm
from sklearn.metrics import accuracy_score
import matplotlib as mpl
import matplotlib.colors
import matplotlib.pyplot as plt
if __name__ == "__main__":
data = pd.read_csv(r'D:\VS-Code-python\ML_algorithm\support_vector_machine\test_data.txt', sep='\t', header=None)
x, y = data[[0, 1]], data[2]
# 分类器
clf_param = (('linear', 0.1), ('linear', 0.5), ('linear', 1), ('linear', 2),
('rbf', 1, 0.1), ('rbf', 1, 1), ('rbf', 1, 10), ('rbf', 1, 100),
('rbf', 5, 0.1), ('rbf', 5, 1), ('rbf', 5, 10), ('rbf', 5, 100))
x1_min, x2_min = np.min(x, axis=0)
x1_max, x2_max = np.max(x, axis=0)
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]
grid_test = np.stack((x1.flat, x2.flat), axis=1)
cm_light = mpl.colors.ListedColormap(['#77E0A0', '#FFA0A0'])
cm_dark = mpl.colors.ListedColormap(['g', 'r'])
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(13, 9), facecolor='w')
for i, param in enumerate(clf_param):
clf = svm.SVC(C=param[1], kernel=param[0])
if param[0] == 'rbf':
clf.gamma = param[2]
title = '高斯核,C=%.1f,$\gamma$ =%.1f' % (param[1], param[2])
else:
title = '线性核,C=%.1f' % param[1]
clf.fit(x, y)
y_hat = clf.predict(x)
print('准确率:', accuracy_score(y, y_hat))
# 画图
print(title)
print('支持向量的数目:', clf.n_support_)
print('支持向量的系数:', clf.dual_coef_)
print('支持向量:', clf.support_)
plt.subplot(3, 4, i+1)
grid_hat = clf.predict(grid_test) # 预测分类值
grid_hat = grid_hat.reshape(x1.shape) # 使之与输入的形状相同
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light, alpha=0.8)
plt.scatter(x[0], x[1], c=y, edgecolors='k', s=40, cmap=cm_dark) # 样本的显示
plt.scatter(x.loc[clf.support_, 0], x.loc[clf.support_, 1], edgecolors='k', facecolors='none', s=100, marker='o') # 支持向量
z = clf.decision_function(grid_test)
# print 'z = \n', z
print('clf.decision_function(x) = ', clf.decision_function(x))
print('clf.predict(x) = ', clf.predict(x))
z = z.reshape(x1.shape)
plt.contour(x1, x2, z, colors=list('kbrbk'), linestyles=['--', '--', '-', '--', '--'],
linewidths=[1, 0.5, 1.5, 0.5, 1], levels=[-1, -0.5, 0, 0.5, 1])
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title(title, fontsize=12)
plt.suptitle('SVM不同参数的分类', fontsize=16)
plt.tight_layout(1.4)
plt.subplots_adjust(top=0.92)
plt.show()
参考资料:
支持向量机通俗导论(理解SVM的三层境界)
《机器学习》——周志华
支持向量机(SVM)——原理篇
拉格朗日对偶性
Python3《机器学习实战》学习笔记(八):支持向量机原理篇之手撕线性SVM
机器学习算法实践-SVM中的SMO算法