『机器学习』 ——主成分分析法(PCA)
文章首发地址见个人博客
主成分分析法
- 一个非监督学习的机器学习算法
- 主要用于数据的降维
- 通过降维,可以发现更便于人类理解的特征
- 其他应用:可视化;去噪
1 主成分分析法
1.1 什么是主成分分析法
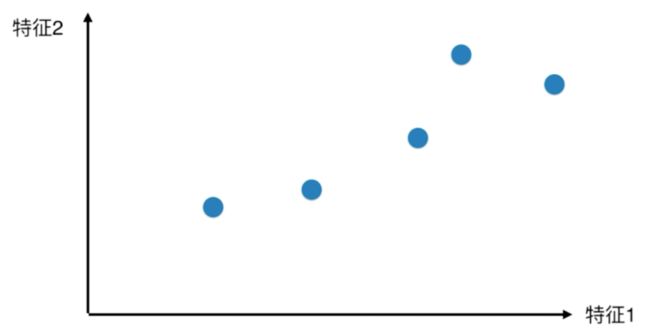
举一个简单的例子,上面的图片中这组数据具有两个特征分别为特征一和特征二,我们如果只考虑其中的一个特征的话,那么就需要将这组数据投影到X轴(特征1)

或Y轴(特征2)上。

比较两种投影结果,我们认为第一种(投影至X轴)的投影效果更好,因为点与点之间的距离比较稀疏,能更好的区分各个样本,反观投影至Y轴上的结果,电与点之间比较紧凑,样本之间不容易区分。

可是这样的投影方式是不是最好的呢?
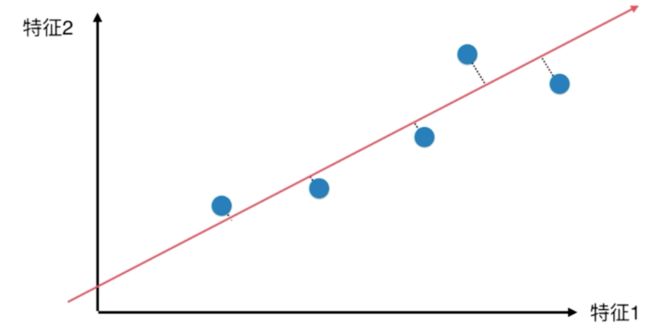
我们继续思考是否存在这样一条直线,当我们把所有的点投影到这条直线上时,所有点之间的距离最大呢?
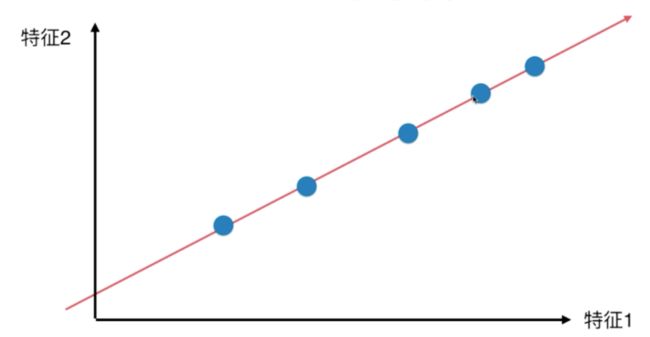
因此我们的目标转换为如何寻找到这样一条让样本间距离最大的轴,但是在这之前,我们应该先知道如何来定义样本间的距离?事实上,在统计学中,方差正好满足我们的需求,它表示样本间整体疏密程度。
V a r ( x ) = 1 m ∑ i = 1 m ( x i − x ˉ ) 2 Var(x)=\frac{1}{m}\sum_{i=1}^m(x_i - \bar{x})^2 Var(x)=m1i=1∑m(xi−xˉ)2
现在我们的问题转化为找到这样的一个轴,使得样本空间中所有的点影射到这个轴之后,方差最大。
第一步:
将所有样本的均值归零(Dmean)
这个操作实质上就是每个样本减去平均值,如此我们原来的坐标系由原来的

转化为了

因为现在的均值已经为零,因此就有了如下公式
V a r ( x ) = 1 m ∑ i = 1 m ( x i − x ˉ ) 2 = 1 m ∑ i = 1 m x i 2 Var(x)=\frac{1}{m}\sum_{i=1}^m(x_i - \bar{x})^2 = \frac{1}{m}\sum_{i=1}^mx_i^2 Var(x)=m1i=1∑m(xi−xˉ)2=m1i=1∑mxi2
第二步:
求一个轴的方向 ( w = ( w 1 , w 2 ) (w = (w_1,w_2) (w=(w1,w2) 使得所有的样本映射到 w w w 以后使得
V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ( X p r o j e c t ( i ) − X ˉ p r o j e c t ) 2 Var(X_{project})=\frac{1}{m}\sum_{i=1}^m(X^{(i)}_{project}-\bar{X}_{project})^2 Var(Xproject)=m1i=1∑m(Xproject(i)−Xˉproject)2
= 1 m ∑ i = 1 m ∣ ∣ X p r o j e c t ( i ) − X ˉ p r o j e c t ∣ ∣ 2 =\frac{1}{m}\sum_{i=1}^m||X^{(i)}_{project}-\bar{X}_{project}||^2 =m1∑i=1m∣∣Xproject(i)−Xˉproject∣∣2
最大,然而经过Dmean处理后 X ˉ p r o j e c t = 0 \bar{X}_{project}=0 Xˉproject=0,所以我们最终的结果为
V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ∣ ∣ X p r o j e c t ( i ) ∣ ∣ 2 Var(X_{project})=\frac{1}{m}\sum_{i=1}^m||X^{(i)}_{project}||^2 Var(Xproject)=m1i=1∑m∣∣Xproject(i)∣∣2

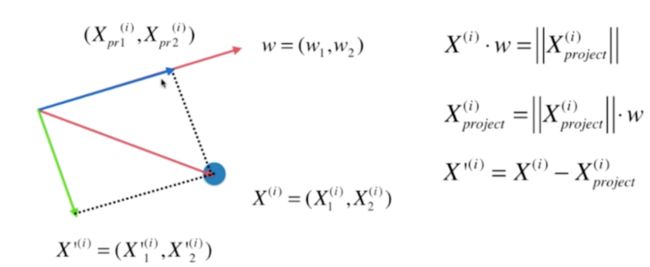
对于一个样本点 X ( i ) = ( X 1 ( i ) , X 2 ( i ) ) X^{(i)}=(X^{(i)}_1,X^{(i)}_2) X(i)=(X1(i),X2(i)),我们将其投影到 w = ( w 1 , w 2 ) w=(w_1,w_2) w=(w1,w2)上,直观的,这其实就是向量点乘的数学意义。因此
∣ X p r o j e c t ( i ) ∣ = X ( i ) ⋅ w = ∣ ∣ X ( i ) ∣ ∣ ⋅ ∣ ∣ w ∣ ∣ ⋅ c o s θ |X_{project}^{(i)}|=X^{(i)}·w=||X^{(i)}||·||w||·cos\theta ∣Xproject(i)∣=X(i)⋅w=∣∣X(i)∣∣⋅∣∣w∣∣⋅cosθ
令 ∣ ∣ w ∣ ∣ = 1 ||w||=1 ∣∣w∣∣=1 ,则有:
∣ X p r o j e c t ( i ) ∣ = ∣ ∣ X ( i ) ∣ ∣ ⋅ c o s θ |X_{project}^{(i)}|=||X^{(i)}||·cos\theta ∣Xproject(i)∣=∣∣X(i)∣∣⋅cosθ
因此现在的目标函数就转换为:
V a r ( X p r o j e c t ) = 1 m ∑ i = 1 m ( X ( i ) ⋅ w ) 2 Var(X_{project})=\frac{1}{m}\sum_{i=1}^m(X^{(i)}·w)^2 Var(Xproject)=m1i=1∑m(X(i)⋅w)2
如何求解这样一个 ( w (w (w 呢,这显然是一个目标函数最优化的问题,我们可以使用梯度上升法来求解。
注意: 在这里我们是预先给定了 ∣ w ∣ = 1 |w|=1 ∣w∣=1这样一个条件,才得到的以上的结果,在具体编程的时候这也是我们需要考虑的地方。
1.2 使用梯度上升法求解主成分分析问题
对于目标函数 1 m ∑ i = 1 m ( X ( i ) ⋅ w ) 2 \frac{1}{m}\sum_{i=1}^m(X^{(i)}·w)^2 m1∑i=1m(X(i)⋅w)2 我们可以将其写成:
f = ∑ i = 1 m ( X 1 ( i ) w 1 + X 2 ( i ) w 2 + ⋯ + X n ( i ) w n ) f=\sum_{i=1}^m(X_1^{(i)}w_1+X_2^{(i)}w_2+\cdots+X_n^{(i)}w_n) f=i=1∑m(X1(i)w1+X2(i)w2+⋯+Xn(i)wn)
下面我们就来求解目标函数的梯度
∇ f = ( ∂ f ∂ w 1 ∂ f ∂ w 2 ⋮ ∂ f ∂ w n ) = 2 m ( ∑ i = 1 m ( X 1 ( i ) w 1 + X 2 ( i ) w 2 + ⋯ + X n ( i ) w n ) X 1 ( i ) ∑ i = 1 m ( X 1 ( i ) w 1 + X 2 ( i ) w 2 + ⋯ + X n ( i ) w n ) X 2 ( i ) ⋮ ∑ i = 1 m ( X 1 ( i ) w 1 + X 2 ( i ) w 2 + ⋯ + X n ( i ) w n ) X n ( i ) ) \nabla f=\begin{pmatrix} \frac{\partial f}{\partial w_1} \\ \frac{\partial f}{\partial w_2} \\ \vdots \\ \frac{\partial f}{\partial w_n} \end{pmatrix} =\frac{2}{m} \begin{pmatrix} \sum_{i=1}^m(X_1^{(i)}w_1+X_2^{(i)}w_2+\cdots+X_n^{(i)}w_n)X_1^{(i)} \\ \sum_{i=1}^m(X_1^{(i)}w_1+X_2^{(i)}w_2+\cdots+X_n^{(i)}w_n)X_2^{(i)} \\ \vdots \\ \sum_{i=1}^m(X_1^{(i)}w_1+X_2^{(i)}w_2+\cdots+X_n^{(i)}w_n)X_n^{(i)} \end{pmatrix} ∇f=⎝⎜⎜⎜⎜⎛∂w1∂f∂w2∂f⋮∂wn∂f⎠⎟⎟⎟⎟⎞=m2⎝⎜⎜⎜⎜⎛∑i=1m(X1(i)w1+X2(i)w2+⋯+Xn(i)wn)X1(i)∑i=1m(X1(i)w1+X2(i)w2+⋯+Xn(i)wn)X2(i)⋮∑i=1m(X1(i)w1+X2(i)w2+⋯+Xn(i)wn)Xn(i)⎠⎟⎟⎟⎟⎞
= 2 m ( ∑ i = 1 m ( X ( i ) w ) X 1 ( i ) ∑ i = 1 m ( X ( i ) w ) X 2 ( i ) ⋮ ∑ i = 1 m ( X ( i ) w ) X n ( i ) ) =\frac{2}{m}\begin{pmatrix} \sum_{i=1}^m(X^{(i)}w)X_1^{(i)} \\ \sum_{i=1}^m(X^{(i)}w)X_2^{(i)} \\ \vdots \\ \sum_{i=1}^m(X^{(i)}w)X_n^{(i)} \end{pmatrix} =m2⎝⎜⎜⎜⎜⎛∑i=1m(X(i)w)X1(i)∑i=1m(X(i)w)X2(i)⋮∑i=1m(X(i)w)Xn(i)⎠⎟⎟⎟⎟⎞
在这里我们可以回忆,跟前面学习梯度下降算法时一样,这里的
( ∑ i = 1 m ( X ( i ) w ) X 1 ( i ) ∑ i = 1 m ( X ( i ) w ) X 2 ( i ) ⋮ ∑ i = 1 m ( X ( i ) w ) X n ( i ) ) \begin{pmatrix} \sum_{i=1}^m(X^{(i)}w)X_1^{(i)} \\ \sum_{i=1}^m(X^{(i)}w)X_2^{(i)} \\ \vdots \\ \sum_{i=1}^m(X^{(i)}w)X_n^{(i)} \end{pmatrix} ⎝⎜⎜⎜⎜⎛∑i=1m(X(i)w)X1(i)∑i=1m(X(i)w)X2(i)⋮∑i=1m(X(i)w)Xn(i)⎠⎟⎟⎟⎟⎞
可以转化为
( X ( 1 ) w , X ( 2 ) w , X ( 3 ) w , ⋯ , X ( m ) w , ) ⋅ ( X 1 ( 1 ) X 2 ( 1 ) X 3 ( 1 ) ⋯ X n ( 1 ) X 1 ( 2 ) X 2 ( 2 ) X 3 ( 2 ) ⋯ X n ( 2 ) X 1 ( 3 ) X 2 ( 3 ) X 3 ( 3 ) ⋯ X n ( 3 ) ⋮ ⋮ ⋮ ⋮ ⋮ X 1 ( m ) X 2 ( m ) X 3 ( m ) ⋯ X n m ) (X^{(1)}w,X^{(2)}w,X^{(3)}w,\cdots,X^{(m)}w,)· \begin{pmatrix} X_1^{(1)} & X_2^{(1)} & X_3^{(1)} & \cdots & X_n^{(1)} \\ X_1^{(2)} & X_2^{(2)} & X_3^{(2)} & \cdots & X_n^{(2)} \\ X_1^{(3)} & X_2^{(3)} & X_3^{(3)} & \cdots & X_n^{(3)} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ X_1^{(m)} & X_2^{(m)} & X_3^{(m)} & \cdots & X_n^{m} \end{pmatrix} (X(1)w,X(2)w,X(3)w,⋯,X(m)w,)⋅⎝⎜⎜⎜⎜⎜⎜⎛X1(1)X1(2)X1(3)⋮X1(m)X2(1)X2(2)X2(3)⋮X2(m)X3(1)X3(2)X3(3)⋮X3(m)⋯⋯⋯⋮⋯Xn(1)Xn(2)Xn(3)⋮Xnm⎠⎟⎟⎟⎟⎟⎟⎞
最终结果我们可以写成:
∇ f = 2 m ⋅ ( X w ) T ⋅ X \nabla f=\frac{2}{m}·(Xw)^T·X ∇f=m2⋅(Xw)T⋅X
运算结果是一个 n × 1 n\times 1 n×1 的向量,我们在进行一下转置操作,得到一个 1 × n 1 \times n 1×n 的向量得到
∇ f = 2 m ⋅ X T ( X w ) \nabla f=\frac{2}{m}·X^T(Xw) ∇f=m2⋅XT(Xw)
1.3 梯度上升实现主成分分析(代码)
import numpy as np
import matplotlib.pyplot as plt
X = np.empty((100,2))
X[:, 0] = np.random.uniform(0., 100., size=100)
X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0., 10., size=100)
plt.scatter(X[:, 0],X[:, 1])
plt.show()

在这里X[:, 0]与X[:, 1]具有一定的线性关系,但是他们都是两个特征,读者不要错误地把他们当成前面我们在学习线性回归时的特征与值之间的关系。
def demean(X):
return X - np.mean(X, axis=0)
X_demean = demean(X)
plt.scatter(X_demean[:, 0],X_demean[:, 1])
plt.show()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XhtkRX2o-1576813880078)(https://peterhuang.oss-cn-beijing.aliyuncs.com/notes_pics/%E4%B8%8B%E8%BD%BD%20(1)].png)
可以看到这一步我们就已经完成了Demean操作
打印看看现在在两个特征上的均值:
print(np.mean(X_demean[:,0]))
print(np.mean(X_demean[:,1]))
#******************运行结果************
# -1.2860823517257814e-14
# 1.7195134205394424e-14
可以看到两个维度上的均值已经近乎等于零。
def f(w, X):
return np.sum((X.dot(w) ** 2)) / len(X)
def df_math(w, X):
return X.T.dot(X.dot(w)) * 2. / len(X)
def df_debug(w, X, epsilon = 0.0001):
res = np.empty(len(w))
for i in range(len(w)):
w_1 = w.copy()
w_1[i] += epsilon
w_2 = w.copy()
w_2[i] -= epsilon
res[i] = (f(w_1, X) - f(w_2, X)) / (2 * epsilon)
return res
def direction(w):
return w / np.linalg.norm(w)
def gradient_ascent(df, X, initial_w, eta, n_iterations=1e4, epsilon=1e-8):
w = direction(initial_w)
cur_iterations = 0
while cur_iterations < n_iterations:
gradient = df(w, X)
last_w = w
w = w + eta * gradient
w = direction(w)
if(abs(f(w, X) - f(last_w, X)) < epsilon):
break
cur_iterations += 1
return w
这里的de_math就是我们通过数学推倒得到的梯度公式,而df_debug是另外一种梯度的计算方式,
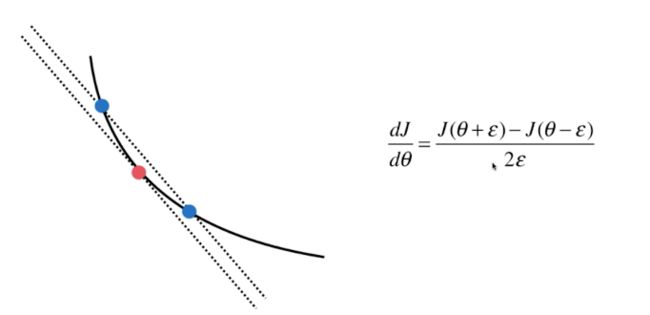
如图所示,我们在计算曲线上某一点的斜率时,在这一点的左右两侧距离 ϵ \epsilon ϵ 的位置各取一点,当 ϵ \epsilon ϵ 足够小的时候,我们就以这两点之间连线的斜率作为所求点的斜率,这其实也就是高等数学中的倒数定义,当 ϵ \epsilon ϵ 的值趋近与零时,两点之间直线的斜率就等于了所求点在曲线上的斜率。我们通常使用这种方法来预估我们的梯度石头计算的正确。df_debug给出了其具体的代码实现。
initial_w = np.random.random(X.shape[1]) #不能从零向量开始
eta = 0.001
#不能使用StandardScaler标准化数据
w = gradient_ascent(df_debug, X_demean, initial_w, eta)
plt.scatter(X_demean[:,0],X_demean[:,1])
plt.plot([0, w[0] * 30], [0, w[1] * 30], color='r')
plt.show()
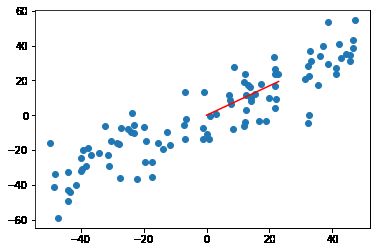
这里需要注意的是,我们在给定一个初始的 w w w 值得时候不能赋值为零向量,因为f(w, X)与df_math(w, X)两个函数都有与 w w w 相乘的运算。而与一个零向量相乘得到的结果为一个零矩阵,这样对于我们的求解没有任何意义,因为每次得到的梯度都是零。再有一点需要注意的是我们在前面使用机器学习算法时,都对数据进行了归一化处理,之前我们使用的是Sci-learn中的StandardScaler来进行数据归一化,而在这里我们不能这样操作,为什么呢?回想一下我们在一开始就是要寻找一个方向向量 w w w 使得我们所有的样本点映射到这个方向之后的方差最大,我们在通过StandardScaler进行归一化处理之后,样本之间的方差就变成了固定的1,又何来最大一说呢?
运行结果如图所示,红色的直线就是我们要找的那一个将所有样本映射到上面方差最大的轴。
2 求数据的前n个主成分
2.1 如何求解下一个主成分?
在求解出第一个主成分之后,如何求解下一个主成分呢?我们的思路是,将数据在第一个主成分上的分量去掉,然后在新的数据上求第一主成分。
我们根据上面的思路来看一下在1.3中的数据去除第一主成分之后是什么样的呢?
X2 = X - X.dot(w).reshape(-1,1) * w
plt.scatter(X2[:,0],X2[:,1])
plt.show()
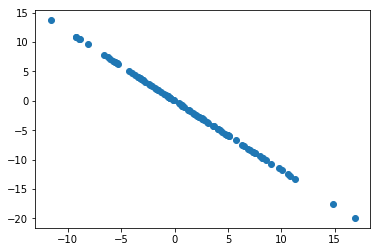
这里X2就是我们去除了第一主成分之后的数据。现在我们用去除了第一主成分的数据来求解第二主成分。
w2 = gradient_ascent(df_debug, X2, initial_w, eta)
print(w.dot(w2))
#*****************运行结果******************
# 1.8437166041551656e-05
这个结果接近于零,所以我们知道,求出来的这两个轴w和w2互相垂直
下面我们写了一个函数first_n_components来实现求一组数据的前n个主成分:
def first_n_components(n, X, eta=0.01, n_iterations=1e4, epsilon=1e-8):
X_pca = X.copy()
X_pca = demean(X_pca)
res = []
for i in range(n):
initial_w = np.random.random(X_pca.shape[1])
w = gradient_ascent(df_math, X_pca, initial_w, eta)
res.append(w)
X_pca = X_pca - X_pca.dot(w).reshape(-1,1) * w
return res
first_n_components(2, X)
#*****************运行结果******************
# [array([0.7630797, 0.6463044]),
array([-0.6463027 , 0.76308113])]
3 高维数据向低维数据映射
3.1 高维数据向低维数据映射
对于一个原始数据 X X X
X = ( X 1 ( 1 ) X 2 ( 1 ) ⋯ X n ( 1 ) X 1 ( 2 ) X 2 ( 2 ) ⋯ X n ( 2 ) ⋮ ⋮ ⋮ ⋮ X 1 ( m ) X 2 ( m ) ⋯ X n ( m ) ) X = \begin{pmatrix} X_1^{(1)} & X_2^{(1)} & \cdots & X_n^{(1)} \\ X_1^{(2)} & X_2^{(2)} & \cdots & X_n^{(2)} \\ \vdots & \vdots & \vdots & \vdots \\ X_1^{(m)} & X_2^{(m)} & \cdots & X_n^{(m)} \\ \end{pmatrix} X=⎝⎜⎜⎜⎜⎛X1(1)X1(2)⋮X1(m)X2(1)X2(2)⋮X2(m)⋯⋯⋮⋯Xn(1)Xn(2)⋮Xn(m)⎠⎟⎟⎟⎟⎞
我们求出其前 k k k 个主成分 w k w_k wk:
W k = ( W 1 ( 1 ) W 2 ( 1 ) ⋯ W n ( 1 ) W 1 ( 2 ) W 2 ( 2 ) ⋯ W n ( 2 ) ⋮ ⋮ ⋮ ⋮ W 1 ( k ) W 2 ( k ) ⋯ W n ( k ) ) W_k = \begin{pmatrix} W_1^{(1)} & W_2^{(1)} & \cdots & W_n^{(1)} \\ W_1^{(2)} & W_2^{(2)} & \cdots & W_n^{(2)} \\ \vdots & \vdots & \vdots & \vdots \\ W_1^{(k)} & W_2^{(k)} & \cdots & W_n^{(k)} \\ \end{pmatrix} Wk=⎝⎜⎜⎜⎜⎛W1(1)W1(2)⋮W1(k)W2(1)W2(2)⋮W2(k)⋯⋯⋮⋯Wn(1)Wn(2)⋮Wn(k)⎠⎟⎟⎟⎟⎞
我们如何求得其降维之后的数据呢?
X k = X ⋅ W k T X_k = X·{W_k}^T Xk=X⋅WkT
我们知道原始数据 X X X 是一个 m × n m \times n m×n 的矩阵,而 W k W_k Wk 是一个 k × n k \times n k×n 的矩阵,经过转置之后就成为了一个 n × k n \times k n×k 的矩阵,两者相乘得到的是一个 m × k m \times k m×k 的矩阵,如此我们就把一个 n n n 维的数据降维成了 k k k 维。
3.2 代码实现
首先我们在这里封装了一个类PCA我们将主成分分析法的一系列处理过程封装进了这个类当中
import numpy as np
class PCA:
def __init__(self, n_components):
"""初始化PCA"""
assert n_components >= 1, "n_components must be valid"
self.n_components = n_components
self.components_ = None
def fit(self, X, eta=0.01, n_iterations=1e4):
"""获取数据集的前n个主成分"""
assert self.n_components <= X.shape[1],\
"n_components must be greater than the feature nunber of X"
def demean(X):
return X - np.mean(X, axis=0)
def f(w, X):
return np.sum((X.dot(w) ** 2)) / len(X)
def df(w, X):
return X.T.dot(X.dot(w)) * 2. / len(X)
def direction(w):
return w / np.linalg.norm(w)
def first_components(X, initial_w, eta=0.01, n_iterations=1e4, epsilon=1e-8):
w = direction(initial_w)
cur_iterations = 0
while cur_iterations < n_iterations:
gradient = df(w, X)
last_w = w
w = w + eta * gradient
w = direction(w)
if(abs(f(w, X) - f(last_w, X)) < epsilon):
break
cur_iterations +=1
return w
X_pca = demean(X)
self.components_ = np.empty(shape=(self.n_components, X.shape[1]))
for i in range(self.n_components):
initial_w = np.random.random(X_pca.shape[1])
w = first_components(X_pca, initial_w, eta, n_iterations)
self.components_[i,:] = w
X_pca = X_pca - X_pca.dot(w).reshape(-1,1) * w
return self
def trasform(self, X):
"""将给定的X映射到各个主成分分量重"""
assert X.shape[1] == self.components_.shape[1]
return X.dot(self.components_.T)
def invers_transform(self, X):
return X.dot(self.components_)
def __repr__(self):
return "PCA(n_components=%d)" % self.n_components
下面我们调用这个类
import numpy as np
from pca import PCA
import matplotlib.pyplot as plt
X = np.empty((100,2))
X[:, 0] = np.random.uniform(0., 100., size=100)
X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0., 10., size=100)
pca = PCA(n_components=2)
pca.fit(X)
print(pca.components_)
pca = PCA(n_components=1)
pca.fit(X)
X_reduction = pca.trasform(X)
X_restore = pca.invers_transform(X_reduction)
plt.scatter(X[:, 0], X[:, 1], color='b', alpha=0.5)
plt.scatter(X_restore[:, 0], X_restore[:, 1], color='r')
plt.show()
#****************运行结果********************
# [[ 0.77494938 0.63202331]
# [ 0.63202665 -0.77494665]]
