数据结构与算法学习
数据结构与算法学习
一 复杂度
1.1 时间复杂度:算法执行效率
算法的执行时间与算法的输入值之间的关系
执行多少次
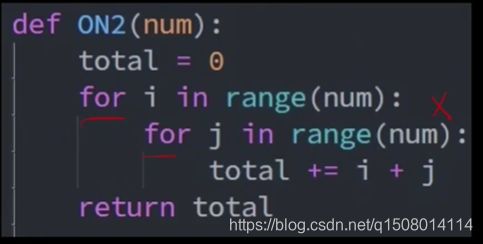
def test():
total=0 #这一段所用时间a
for i in range(num):
total+=i #这一段所用时间b
return total #这一段所用时间c
a+10b+c 这个受num的影响,当num较大时,忽略a,c;时间复杂度n b,,b相当于系数,O(N)
计算时间复杂度时,看程序是否有while for 循环。如果没有,一般为O(1)
1.2 一般的时间复杂度案例:
O(1) 表示算法执行时间与num没有关系
O(n)
O(log n)
def f(num):
i=1
while (i<num)
i=i*2
return i
解释:num为N个,每次执行时间为a .执行次数为x,2^x=N,故x=log N. alog N,忽略系数a,得log N。
O(m+n)
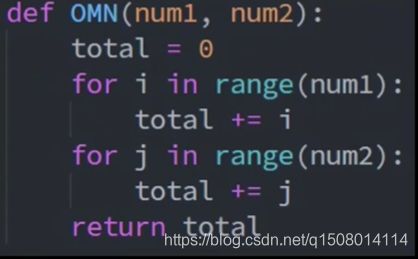
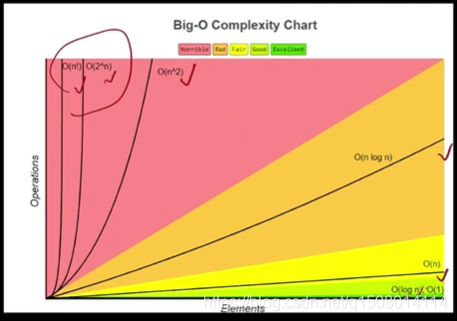
时间复杂度排序:
O(n) < O(log n) < O(n) < O(n log n)
一般优化算法时,可以从降低时间复杂度角度分析。
2 .1空间复杂度:
空间复杂度:算法存储空间与输入值之间的关系。
声明的变量会占空间。
会占多少块空间

O(1 ) O(N )
2.2 常用空间复杂度
O(1) O(n) O( n^2)
二 数据结构1—数组
1 数组访问、数组搜索、插入数组、删除数组

数组是一个 适合读、不适合写的数据结构。
2 python数组常用操作
a.append() #添加元素【尾部】
a[2]
for index,element in enumerate(a):#即返回索引、值
#查找数组a某个元素的索引
a.index(2)
数组排序的时间复杂度O(N log N)
三 数据结构2–链表
3.1 数组:数值存在 连续 的内存空间…
不连续的内存空间存储,故提供了一种新的数据结构—链表
3.2 比较一个数据结构的好与坏,关键在于访问、搜索、插入、删除元素时的时间复杂度 O(N) O(N) O(1) O(1)
在链表中访问元素
单端链表
故写的块,读的慢不适合读,适合写
链表的每个节点里有两个属性:val,next
链表的python常用操作:
常用包deque
创建链表 linkedlist=deque()
添加元素linkedlist.append(1)#在末尾添加
linkedlist.insert(2,99)#在指定位置添加元素,第一个参数:索引的位置;第二个参数:元素值
访问元素 linkedlist[2]
查找元素linkedlist.index(99)99这个值对应的索引
更新元素 linkedlist[2]=88
删除元素linkedlist.remove(6)#参数为数值,不是索引
先遍历找到这个数,–O(N) ;在删除—O(1)
链表长度 len(linkedlist)
3.3 链表练习题:
203移除链表元素,
206反转链表
首先,关于单链表中的环,一般涉及到一下问题:
1.给一个单链表,判断其中是否有环的存在; 力扣141
最容易想到的方法是遍历所有节点,每次遍历到一个节点时,判断该节点此前是否被访问过。
可以使用哈希表来存储所有已经访问过的节点。每次我们到达一个节点,如果该节点已经存在于哈希表中,则说明该链表是环形链表,否则就将该节点加入哈希表中
```python
class Solution:
def hasCycle(self, head: ListNode) -> bool:
if head==None or head.next==None:
return False
#采用快慢指针进行
slow=head
fast=head.next
while slow!=fast:
if fast==None or fast.next==None:
return False
slow=slow.next
fast=fast.next.next
return True
2.如果存在环,找出环的入口点;力扣142
解析: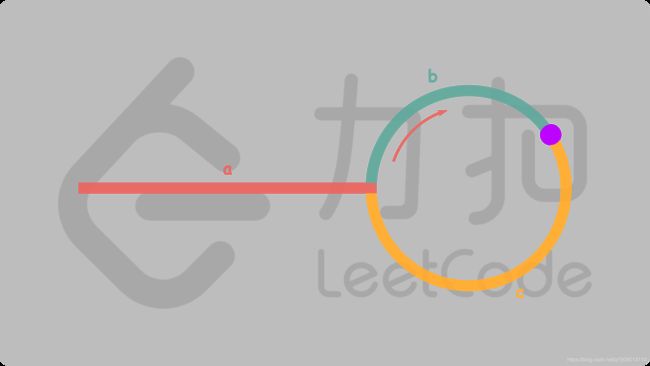
(一)设链表中环外部分的长度为 a。slow 指针进入环后,又走了 b的距离与fast 相遇。此时,fast 指针已经走完了环的 n 圈,因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nca+n(b+c)+b=a+(n+1)b+nc
(二)任意时刻,fast 指针走过的距离都为slow 指针的 22 倍。因此,我们有
a+(n+1)b+nc=2(a+b) \implies a=c+(n-1)(b+c)
a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)
(三)从相遇点到入环点的距离加上 n-1 圈的环长,恰好等于从链表头部到入环点的距离
class Solution:
def detectCycle(self, head: ListNode) -> ListNode:
#链表存在环,找出环的入口点
#先判断是否存在环
if head == None or head.next==None:
return None
slow = head
fast = head
#循环条件里的终止条件、条件判断很重要
while fast!=None:
slow = slow.next
if fast.next != None:
fast=fast.next.next
else:
return None
if fast==slow:
ptr = head
while ptr!=slow:
ptr = ptr.next
slow = slow.next
return ptr;
return None
3.如果存在环,求出环上节点的个数;
4.如果存在环,求出链表的长度;
5.如果存在环,求出环上距离任意一个节点最远的点(对面节点);
6.(扩展)如何判断两个无环链表是否相交;
7.(扩展)如果相交,求出第一个相交的节点; 力扣1925、160
利用快慢指针。如果有相交,则说明从相交部分开始后半部分相同;据此,得到不同链表的长度,并利用快慢指针将链表的head对其,同时移动比较。
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
#依旧采用快慢指针思路
#计算各个链表的长度
a=headA
count1=0
while a!=None:
count1=count1+1
a=a.next
b=headB
count2=0
while b!=None:
count2=count2+1
b=b.next
a=headA
b=headB
if count1>=count2:
for i in range(count1-count2):
a=a.next
if count1<count2:
for i in range(count2-count1):
b=b.next
#循环条件比较重要
while a!=None and b!=None:
if a==b:
return a
break
a=a.next
b=b.next
return None
原文链接:https://blog.csdn.net/doufei_ccst/article/details/10578315
3.4 python实现链表数据结构
[python-链表](https://zhuanlan.zhihu.com/p/60057180)
四 数据结构3---队列Queue
1 特点:先入先出
2 单端队列:只有一个口可以进,一个口可以出
双端队列
3 研究一个数据结构的特点
3.1 访问access o(n)
3.2 搜索search o(n)
3.3 插入insert o(1)
3.4 删除remove o(1)
4 队列常用操作
我们都知道queue是队列,deque也是队列,不过稍稍特殊一些,是双端队列。对于queue来说,只允许在队尾插入元素,在队首弹出元素。而deque既然称为双端队列,那么说明它的队首和队尾都支持元素的插入和弹出。相比于普通的队列,要更加灵活一些。
[python的库collections的deque操作详解](https://zhuanlan.zhihu.com/p/110476502)
4.1 创建队列 python的内置函数
```python
from collections import deque
queue = deque()
添加元素 queue.append(1) ;queue.append(2) ;queue.append(3)
queue为 [1,2,3]
获取即将出队的元素 a=queue[0]
删除即将出队的元素 b=queue.popleft() b为 [2,3]
判断队列是否为空
队列长度 len(queue)
遍历队列(边删除边遍历队列操作)
while len(queue)!=0:
temp=queue.pop
queue.popleft()
print (temp)
5 练习题
933 最近的请求次数
最近的请求次数
在构造函数中,self的使用
错误代码示范
from collections import deque
class RecentCounter:
#构造函数:定义队列
def __init__(self):
Q=deque()
def ping(self, t: int) -> int:
Q.append(t)
while (len(Q)>0 and Q[0]<t-3000):
Q.popleft()
return len(Q)
正确代码
from collections import deque
class RecentCounter:
#构造函数:定义队列
def __init__(self):
self.Q=deque()
def ping(self, t: int) -> int:
self.Q.append(t)
while (len(self.Q)>0 and self.Q[0]<t-3000):
self.Q.popleft()
return len(self.Q)
239 滑动窗口的最大值
五 数据结构4—栈
栈:先进后出
1 研究一个数据结构的特点
1.1 访问access o(1) 仅仅访问栈顶元素
1.2 搜索search o(n)
1.3 插入insert o(1)
1.4 删除remove o(1) 仅仅删除栈顶元素
2 栈常用操作
创建栈 python的内置函数
stack=[] or stack=list() # **使用列表构造栈数据结构**
添加元素 stack.append(1) ; stack.append(2) ; stack.append(3)
stack为 [1,2,3]
获取栈顶元素 a= stack[-1] #从后往前读
删除栈顶元素 b=stack.pop() b为 3 stack为[1,2]
判断栈是否为空 len(stack)==0
栈长度 len(stack)
遍历栈(边删除边遍历栈操作)
while len(stack)>0:
temp=stack.pop()
print (temp)
3 练习题
充分利用到 栈后进先出的特点
20 有效的括号
class Solution:
def isValid(self, s: str) -> bool:
if len(s)==0:
return 'True'
else:
#初始化一个栈
a=stack()
for c in s:
if c=='(' or c=='[' or c=='{':
a.append(c)
else:
if len(a)==0:
return 'False'
else:
#获取栈顶元素
temp=a.pop()
if c==')':
if temp!='(':
return 'False'
if c==']':
if temp!='[':
return 'False'
if c=='}':
if temp!='{':
return 'False'
if len(a)==0:
return 'True'
else:
return 'False'
496 下一个更大的元素
class Solution:
def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
res=[]
a=list()
for i in nums2:
a.append(i)
for i in nums1:
temp=list()
isFound=False
max_value=-1
while (len(a)!=0 and isFound!= True):
top=a.pop()
if top>i:
max_value=top
if top==i:
isFound=True
temp.append(top)
res.append(max_value)
while len(temp)!=0:
a.append(temp.pop())
return res
六 数据结构5—哈希表Hash Table[散列表]
简单来说,通过键:值来存放 学号:姓名,如果查找某个学号对应的姓名,则需要遍历;
于是,设计一种方法:将键 转化为索引,通过索引直接查找姓名。
python中—字典就是一种哈希表。
key—哈希函数—内存地址—key/vaue对应的内存地址
哈希碰撞:2个不同的key通过同一个哈希函数得到相同的内存地址。
1 研究一个数据结构的特点
1.1 访问access 没有
1.2 搜索search o(1) 对key搜索
1.3 插入insert o(1)
1.4 删除remove o(1)
2 哈希表常用操作
2.1 创建哈希表 python的内置函数
#第一种:直接用数组创建哈希表,索引当作哈希表的key
hashTable=[‘’]*4 #表示哈希表有四个元素,默认值为空字符串
#第二种:用字典创建哈希表
maping={} 或者mapping=dict()
2.2 添加元素
#第一种:在用数组创建的哈希表里添加元素
hashTable=[‘’]*4 #表示哈希表有四个元素,默认值为空字符串
hashTable[1]='韩梅梅'
hashTable[2]=‘李华’
#第二种:用字典的创建的哈希表里添加元素
maping={} 或者mapping=dict()
maping[1]='韩梅梅'
maping[2]=‘李华’
修改元素
2.3 删除元素
#用字典的创建的哈希表 删除元素
maping.pop(1)
del mapinng[1]
2.4 获取key的值
直接访问key
2.5 检查key是否存在
#用字典的创建的哈希表
3 in maping #返回Ture或者False
2.6 哈希表的长度
哈希表是否有元素
#用字典的创建的哈希表
len(maping) #返回Ture或者False
3 练习题
217 存在重复元素
389 找不同
标记:217与389 第一次都是使用python的字典进行解决的;利用key:value形式进行统计个数
496 下一个最大元素
七 数据结构6—集合set
7.1 无序,不重复
作用:查看元素是否存在,是否重复
7.2 集合的类型:HashSet\LinklistSet\Tree Set
7.3 HashSet
s=set() #创建集合
s.add() #添加元素
s.remove(2) #移除元素
len(s) #长度
7.4 练习题
217
705
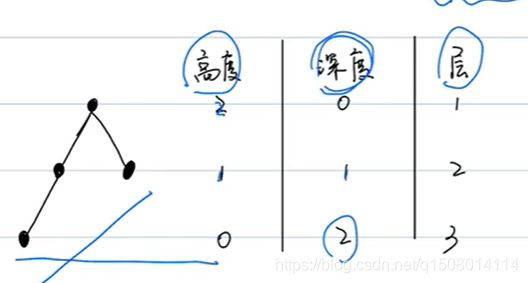
八 数据结构7—树【具备父子关系】
节点
根节点【唯一 一个】
叶子节点【没有孩子的节点 为叶子节点】
7.1 二叉树:每个节点最多只能有俩个个孩子
满二叉树:除了叶子节点,每个节点都有 左右两个孩子;所有叶子节点在同一层上
完全二叉树: 从树的根节点,从上到下、从左到右依次填满节点形成的二叉树
(1)二叉树的遍历
从根节点开始遍历,用拆分思想理解
前序遍历:根节点—左子树—右子树
中序遍历:左子树—根节点—右子树
后序遍历:左子树—右子树—根节点
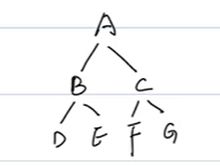
前序遍历:A-B-D-E-C-F-G
中序遍历:D-B-E-A-F-C-G
后序遍历:D-E-B-F-G-C-A
(2)树的常用操作
(3)练习题
144 二叉树前序遍历
94 二叉树中序遍历
145 二叉树后序遍历
九 数据结构8—堆Heap
一种二叉树的结构
完全二叉树
每个节点>= 或者 <=孩子节点
十 数据结构9—图【Graph】
树:类似于父子关系
图:类似于邻居关系
顶点、邻居顶点、度、
无向图
有向图:入度、出度
权重图—最短路径
十一 经典算法