代码随想录刷题】Day16 二叉树03

• 【104】二叉树的最大深度
• 【111】二叉树的最小深度
  • 【559】N叉树的最大深度
• 【222】完全二叉树的节点个数

1.【104】二叉树的最大深度（优先掌握递归）

【104】二叉树的最大深度

1.1 前言

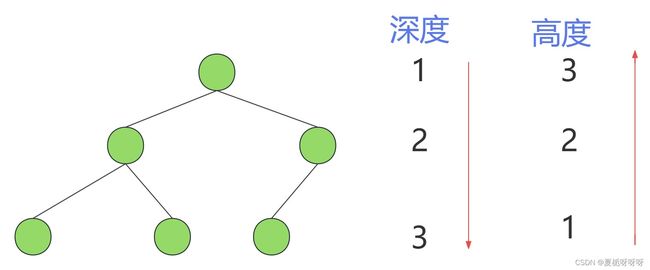
• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）
• 前序求深度，后序求高度。

如图所示：

1.2 题目描述

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

1.3 递归法java代码实现

我们知道了二叉树的深度和高度，那么根节点的高度就是二叉树的最大深度，所以本题中我们可以通过后序遍历求的根节点高度来求二叉树的最大深度。

此题的递归三部曲

• 1. 确定递归函数的参数和返回值

参数就是传入的树的根节点，返回这棵树的深度，所以返回值类型是int型

public int getDepth(TreeNode node)

• 2. 确定终止条件

如果为空节点的话，就返回0，表示高度为0。

if (root == null) {
	return 0;
}

• 3. 确定单层递归的逻辑

先求它的左子树的深度，再求右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。

int leftDepth=maxDepth(root.left);
int rightDepth=maxDepth(root.right);
int depth=Math.max(leftDepth,rightDepth)+1;
return depth;

整体代码如下：

class solution {
    /**
     * 递归法
     */
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);
        return Math.max(leftDepth, rightDepth) + 1;
    }
}

1.4 迭代法java代码实现

使用迭代法的话，使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。

在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：

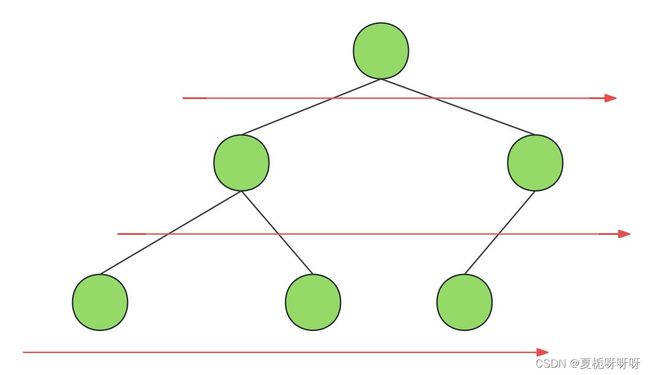
所以这道题的迭代法就是一道模板题，可以使用二叉树层序遍历的模板来解决的。

	/**
     * 迭代法
     */
class Solution {
    public int maxDepth(TreeNode root) {
        Queue<TreeNode> que=new LinkedList<>();
        if (root==null){
            return 0;
        }
        
        que.offer(root);
        int depth=0;//深度
        while (!que.isEmpty()) {
            int len=que.size();
            for (int i=0;i<len;i++){
                TreeNode tempNode=que.poll();
                if (tempNode.left!=null){
                    que.offer(tempNode.left);
                }
                if (tempNode.right!=null){
                    que.offer(tempNode.right);
                }
            }
            depth++;
        }
        return depth;

    }
}

1.5 相关练习题【559】N叉树的最大深度

【559】N叉树的最大深度

class Solution {
    public int maxDepth(Node root) {
         if (root==null){
            return 0;
        }
        int maxChildDepth=0;
        List<Node> children=root.children;
        for (Node child : children) {
            int childDepth=maxDepth(child);
            maxChildDepth=Math.max(maxChildDepth,childDepth);
        }
        return maxChildDepth+1;
    }
}

2.【111】二叉树的最小深度（优先掌握递归）

【111】二叉树的最小深度

2.1 题目描述

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

2.2 递归法java代码实现

此题的重点在于读懂题意，理解最小深度 ，最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

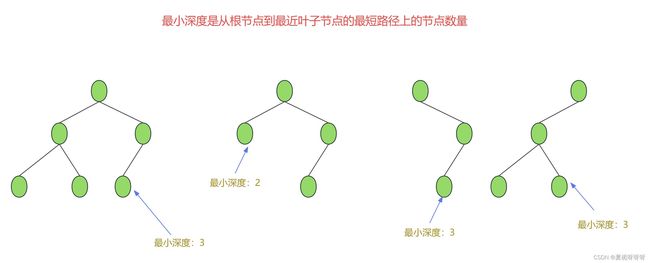
递归三部曲：

• 1.确定递归函数的参数和返回值

参数为要传入的二叉树根节点，返回的是int类型的深度。

public int getDepth(TreeNode node)

• 2.确定终止条件

终止条件也是遇到空节点返回0，表示当前节点的高度为0。

		if (node==null){
            return 0;
        }

• 3.确定单层递归的逻辑
  • 如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。
  • 右子树为空，左子树不为空，最小深度是 1 + 左子树的深度
  • 最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

遍历的顺序为后序（左右中），可以看出：求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩子不为空的逻辑。

整体代码如下：

class Solution {
    public int minDepth(TreeNode root) {
        return getDepth(root);

    }
    public int getDepth(TreeNode node){
        if (node==null){
            return 0;
        }
        int leftDepth=getDepth(node.left);
        int rightDepth=getDepth(node.right);

        //当一个左子树为空，右不为空，这时不是最低点
        if (node.left==null && node.right!=null){
            return rightDepth+1;
        }
        //当一个右子树为空，左不为空，这时不是最低点
        if (node.left!=null && node.right==null){
            return leftDepth+1;
        }
        int result=Math.min(leftDepth,rightDepth)+1;
        return result;
    }
}

2.3 迭代法 java代码实现

相对于 【104】二叉树的最大深度，本题还也可以使用层序遍历的方式来解决，思路是一样的。

需要注意的是，只有当左右孩子都为空的时候，才说明遍历的最低点了。 如果其中一个孩子为空则不是最低点。

class Solution {
    public int minDepth(TreeNode root) {
    //迭代法
        /**
         * 相对于 104.二叉树的最大深度 ，
         * 本题还也可以使用层序遍历的方式来解决，思路是一样的。
         *
         * 需要注意的是，只有当左右孩子都为空的时候，才说明遍历的最低点了。
         * 如果其中一个孩子为空则不是最低点
         */
        Queue<TreeNode> que = new LinkedList<>();
        if (root == null) {
            return 0;
        }

        que.offer(root);
        int depth = 0;
        while (!que.isEmpty()){
            int len = que.size();
            depth++;
            TreeNode tempNode = null;
            for (int i = 0; i < len; i++) {
                tempNode = que.poll();
                //如果当前节点的左右孩子都为空，直接返回最小深度
                if (tempNode.left == null && tempNode.right == null){
                    return depth;
                }
                if (tempNode.left != null) que.offer(tempNode.left);
                if (tempNode.right != null) que.offer(tempNode.right);
            }
        }
        return depth;

    }
}

3.【222】完全二叉树的节点个数

【222】完全二叉树的节点个数

3.1 题目描述

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^h 个节点。

提示：

• 树中节点的数目范围是[0, 5 * 10⁴ ]
• 0 <= Node.val <= 5 * 10⁴
• 题目数据保证输入的树是 完全二叉树

3.2 java代码实现

class Solution {
    // 通用递归解法
    public int countNodes(TreeNode root) {
        if(root == null) {
            return 0;
        }
        return countNodes(root.left) + countNodes(root.right) + 1;
    }
}

class Solution {
    // 迭代法
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int result = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size -- > 0) {
                TreeNode cur = queue.poll();
                result++;
                if (cur.left != null) queue.offer(cur.left);
                if (cur.right != null) queue.offer(cur.right);
            }
        }
        return result;
    }
}