粒子群算法(Particle Swarm Optimization,PSO)介绍及MATLAB代码
目录
-
- 前言
- PSO简介
- classical PSO分类
- 全局版粒子状态更新公式
- 算法流程
- 参数设置
- MATLAB代码
- 实验结果展示
前言
本文主要介绍了典型的粒子群算法流程以及给出了求解函数极值时的matlab代码。
PSO简介
1. 由Eberhart和Kennedy于1995年提出。
2. 早期简单的模型,即Boid(Bird-oid)模型,模拟鸟群觅食行为而建:
每一个鸟的个体用直角坐标系上的点表示,随机地给它们赋一个初速度和初位置,程序运行的每一步都按照“最近邻速度匹配”规则,且在速度项中增加了一个随机变量,即在迭代的每一步,除了满足“最近邻速度匹配”之外,每一步速度还要添加一个随机变化的量,这样使得整个模拟看起来更为真实。
3. 粒子群算法是一种基于种群的搜索过程,其中每个个体称作微粒,定义为在D维搜索空间中待优化问题的潜在解,保存有其历史最优位置和所有粒子的最优位置的记忆,以及速度。在每一演化代,微粒的信息被组合起来调整速度关于每一维上的分量,继而被用来计算新的微粒位置。微粒在多维搜索空间中不断改变它们的状态,直到到达平衡或最优状态,或者超过了计算限制为止。问题空间的不同维度之间唯一的联系是通过目标函数引入的。很多经验证据已经显示该算法是一个非常有效的优化工具。
classical PSO分类
经典的PSO可分为:
- 全局版:微粒跟踪的两个极值为自身最优位置pBest和种群最优位置gBest
- 局部版:微粒除了追随自身最优位置pBest之外,不跟踪种群最优位置gBest,而是跟踪拓扑邻域中的所有微粒的最优位置nBest
全局版粒子状态更新公式
每个粒子找到个体极值pBest和全局极值gBest,更新粒子速度和位置:
- 更新速度:v[t+1] = w * v[t] + c1 * rand() * (pBest[i] - present[t]) + c2 * rand() * (gBest[i] - present[t]) ;
- 更新位置:present[t+1] = present[t] + v[t];
- 其中:v[] 是粒子的速度, w是惯性权重,present[] 是当前粒子的位置. pbest[]是个体极值,gbest[]是全局极值, rand () 是介于(0,1)之间的随机数. c1, c2 是学习因子.
- 注:局部版只需将公式中gBest替换为nBest
算法流程
- 种群随机初始化(初始种群中个体的位置x和速度v,其中个体位置就是优化问题中的解);
- 对每一个粒子计算初始适应值f(x),得到粒子本身的初始最优解pBest;
- 寻找种群全部粒子中的初始最优解gBest;
- 对每个粒子计算本次循环中的移动距离(即移动速度),更新粒子所在位置,即将算得的移动速度累加在原来的粒子位置上,(更新公式见全局版粒子状态更新公式);
- 对每一个粒子计算当前适应值f(x),得到粒子本身的最优解pBest;
- 寻找种群全部粒子中的最优解gBest;
- 判断是否满足终止条件,满足则停止,否则从步骤 4 继续循环迭代。
参数设置
- 粒子数(种群规模):一般取 20 – 40. 其实对于大部分的问题10个粒子已经足够可以取得好的结果, 不过对于比较难的问题或者特定类别的问题, 粒子数可以取到100 或 200。
- 粒子的长度:这是由优化问题决定, 就是问题解的长度。
- 粒子的位置范围:由优化问题决定,每一维可以设定不同的范围。
- 最大速度:决定粒子在一个循环中最大的移动距离,通常设定为粒子的范围宽度的10%-40%,例如粒子 的某一维位置范围属于 [-10, 10], 那么 最大速度Vmax 的大小可以是 2。
- 学习因子: c1 和 c2 通常等于 2. 不过在文献中也有其他的取值. 但是一般 c1 等于 c2 并且范围在0和4之间。学习因子c1和c2代表了将每个微粒拉向pBest和gBest(或nBest)位置的随机加速项的权重。
若把 c1 设置为零,衍变出只有社会模型( The Social-only Model) PSO算法,把 c2 设置为零,衍变出只有认知模型( The Cognition-only Model)PSO算法。 而只有社会模型PSO算法以比较快的速度收敛,但是容易陷入局部最优,特别是对比较复杂的问题。 - 惯性权重:当Vmax很小时,使用接近于1的惯性权重;当Vmax不是很小时,使用权重w=0.6-0.75较好.如果没有Vmax的信息,使用0.8作为权重也是一种很好的选择.惯性权重w很小时偏重于发挥粒子群算法的局部搜索能力;惯性权重很大时将会偏重于发挥粒子群算法的全局搜索能力,速度和位置更新幅度大,偏离原先寻优轨道的程度越大。
- 终止条件:最大循环数或者最小允许误差。
参数可设置为固定值,自适应变化,模糊等。
MATLAB代码
测试用例为CEC’17 Benchmark,代码中函数 [] = feval(fhd,x,varargin{:});是调用算例计算粒子的适应值,varargin{:} 指算例编号(第几个)。
The C and Matlab codes for CEC’17 test suite can be downloaded from the website given below:
https://www.ntu.edu.sg/home/epnsugan/
具体代码如下,包括了全局版和局部版PSO,只需要更改输入参数A即可,A是方阵,表示粒子的拓扑邻域结构。
function [position,fit_value]=PSO_func2(fhd,c1,c2,w_max,w_min,D,particlesize,iterations,xmax,A,varargin)
%PSO参数、粒子速度和位置初始化
% position 粒子全局极值位置
% fit_value 全局极值适应度
% fhd = str2func('cec17_func');
% c1 学习因子(个体极值pBest)
% c2 学习因子(全局极值gBest)
% w_max w_min 惯性因子(本代码采用的是线性递减的权重因此有范围限制)
% D 目标函数自变量个数(维数)
% particlesize 粒子群规模
% iterations 最大迭代次数
% xmax 粒子运动范围(问题的自变量范围)
% A 方阵表示粒子的拓扑结构,A是全连通(所有元素为1)则更新速度和公式时采用的全局版,否则是局部版
varargin 指算例编号(第几个)
%初始化粒子
xmax = repmat(xmax,D,particlesize);
vmax = xmax*0.3; %限制粒子最大速度,太大可能飞出范围
x = -xmax+2*xmax.*rand(D,particlesize); %粒子初始位置,随机数
v = -vmax+2*vmax.*rand(D,particlesize); %粒子初始速度,随机数
%初始化个体极值和全局极值
personalbest_x = x;
personalbest_faval = feval(fhd,x,varargin{:});
[globalbest_new_faval,global_new_i] = min(personalbest_faval);
globalbest_new_x=personalbest_x(:,global_new_i);
%初始化邻域极值
temp = A.*repmat(personalbest_faval',1,particlesize);
[nBest_faval,index] = min(temp);
nBest_x = x(:,index);
%迭代循环
k = 1;
while k<=iterations %终止条件
if k<iterations
w = w_max-k*(w_max-w_min)/iterations;%权重线性递减
else
w = w_min;
end
% w=0.6;%固定权重也可以
%更新粒子群里每个个体的最新速度和位置
v = w*v+c1*rand(D,particlesize).*(personalbest_x-x)+c2*rand(D,particlesize).*(nBest_x-x);
v = (v>vmax).*vmax+(v<(-vmax)).*(-vmax)+(v<=vmax).*(v>=-vmax).*v; %避免超出速度最大值
x = x+v;
%超出x范围则重新分配
x = (x>xmax).*(-xmax+2*xmax.*rand(D,particlesize)) + (x<-xmax).*(-xmax+2*xmax.*rand(D,particlesize)) + (x<=xmax).*(x>=-xmax).*x;
% x = (x>xmax).*(xmax) + (x<-xmax).*(-xmax) + (x<=xmax).*(x>=-xmax).*x;
%个体极值
f=(feval(fhd,x,varargin{:}));
flag = f<personalbest_faval;
personalbest_faval = flag.*f+(1-flag).*personalbest_faval;
flag = repmat(flag,D,1);
personalbest_x = flag.*x+(ones(D,particlesize)-flag).*personalbest_x;
%邻域内极值
temp = A.*repmat(personalbest_faval',1,particlesize);
[nBest_faval,index] = min(temp);
nBest_x = x(:,index);
%全局极值
[globalbest_new_faval,global_new_i] = min(personalbest_faval);
globalbest_new_x=personalbest_x(:,global_new_i);
globalbest(k,1)=k;
globalbest(k,2)=globalbest_new_faval;
k=k+1; %循环计数器+1
end
position = globalbest_new_x;
fit_value = globalbest_new_faval;
%结果输出
% value1 = position;%粒子位置
% value1 = num2str(value1);
% disp(strcat('the corresponding coordinate','=',value1));
% value2 = fit_value;%适应度
% value2 = num2str(value2);
% disp(strcat('the minimum value','=',value2));
%全局极值变化过程图像绘制趋势
% if mod(k,5)==1
% figure(1);
% plot(globalbest(:,1),globalbest(:,2));
% end
% ylabel('适应值');
% xlabel('迭代次数');
%二维自变量的图像输出
scale=2;
if D==2
figure(2);
a=-xmax:scale:xmax;
b=a;
[a,b]=meshgrid(a,b);
for i=1:(2*xmax/scale+1)
for j=1:(2*xmax/scale+1)
c=[a(i,j);b(i,j)];
y(i,j)=feval(fhd,c,varargin{:});
j=j+1;
end
i=i+1;
end
mesh(a,b,y);%画三维图
view([-30,50]);%调整图的视角
hold on;
plot3(position(1),position(2),fit_value,'rp','linewidth',2);%标出极点
legend('目标函数','搜索到的最大值');
xlabel('x'),ylabel('y'),zlabel('目标值');
end
实验结果展示
收敛性
CEC benchmark中第5个算例求解收敛曲线如下:

CEC benchmark中部分算例结果展示如下:
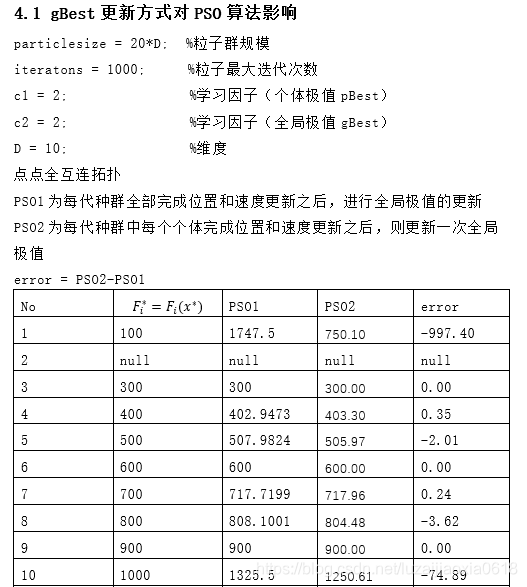
可以看出来大多数情况下PSO具有较好性能,但众所周知no free lunch定理,不可能对所有算例都是最好的。