带头双向循环链表详解
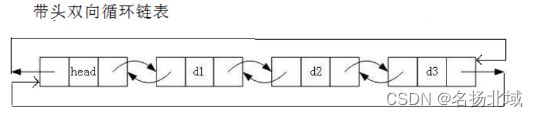
带头双向循环链表详解
- 前言
- 双向链表的结构
- 定义结点
- 初始化链表
-
- 开辟一个新结点
- 初始化
- 链表打印
- 链表尾插
- 头插数据
- 尾删数据
- 头删数据
- 链表查找数据
- 在pos位置前面插入数据
- 删除pos位置的数据
- 链表销毁
- 最后总结
前言
前面讲解了不带头单向非循环链表,今天介绍另一种结构,带头循环双向链表。与之前的单链表对比,这是一种近乎完美的结构,从后面的对比可以看出,关于单向链表的讲解大家如果有兴趣可以看看这篇文章。
链接:单向链表详解
双向链表的结构
无头单向非循环链表:结构简单,一般不会用来存储数据。实际上更多是作为其他数据结构的子结构,如哈希桶、图的链接表等等。此外,这种结构在笔试面试中出现很多。
带头双向循环链表:结构最复杂,一般用在单独存储数据。实际中使用的链表数据结构都是带头双向循环链表。另外,这个结构虽然复杂,但是使用代码实现以后会发现结构会带来很多优势。实现反而简单了。
定义结点
typedef int LTDataType;
typedef struct ListNode
{
struct ListNode* prev;
LTDataType data;
struct ListNode* next;
}LTNode;
初始化链表
定义一个头结点,这个头节点是不用来存放任何数据的。这个结点我们也叫做哨兵卫。
开辟一个新结点
封装成一个函数方便后面写代码
LTNode* BuyLTNode(LTDataType x)
{
LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->data = x;
newnode->next = NULL;
newnode->prev = NULL;
return newnode;
}
初始化
LTNode* LTInit()
{
LTNode* phead = BuyLTNode(-1);
phead->data = -1;
phead->prev = phead;
phead->next = phead;
return phead;
}
开辟一个头节点,它的next和prev都指向自己使得链表一开始就满足循环的条件。
注意,这个时候必须要返回哨兵卫结点的地址,如果不返回的话,就要传二级指针。
链表打印
void LTPrint(LTNode* phead)
{
assert(phead);
//哨兵卫没有存放有效数据,应该从头节点下一个结点开始打印
LTNode* cur = phead->next;
printf("guard<==>");
while (cur != phead)
{
printf("%d<==>", cur->data);
cur = cur->next;
}
printf("\n");
}
链表尾插
前面提到双向链表是一个特别完美的链表,现在看看它在尾插时的优势。
void LTPushBack(LTNode* phead, LTDataType x)
{
LTNode* tail = phead->prev;
//把开辟一个新结点封装成一个函数,并且返回这个结点的地址
LTNode* newnode = BuyLTNode(x);
tail->next = newnode;
newnode->prev = tail;
newnode->next = phead;
phead->prev = newnode;
}
1.不用分为空链表和非空链表两种情况插入。
之前写单链表的时候根据要改变结构体的指针还是改变结构体的成员分为空链表和非空链表两种情况。而双向链表有哨兵卫的情况尾插的时候永远不会改变头结点的指针,所以传参的时候只用传一级指针就可以了。
2.时间复杂度进一步提高
如果是单链表的尾插数据的时候要找到单链表尾结点,需要遍历一遍链表,时间复杂度为o(N).
而双向链表的话,直接可以通过phead->prev找到尾结点
下面测试一下
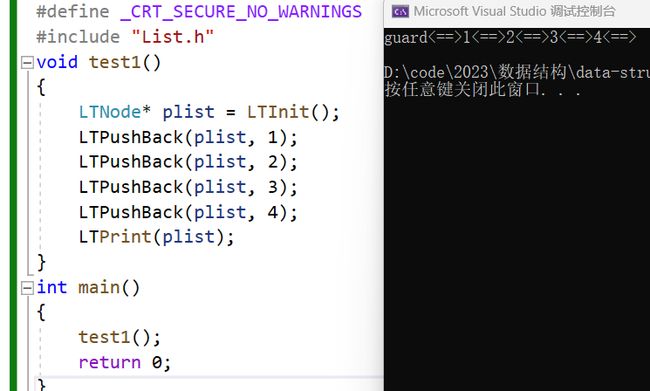
所以可以看出尾插时双向链表相较于单向链表,不仅仅逻辑更清晰,代码更加 简洁,效率也更高 。
记得要对phead断言,phead不能为NULL;
头插数据
void LTPushFront(LTNode* phead, LTDataType x)
{
assert(phead);
LTNode* newnode = BuyLTNode(x);
newnode->next = phead->next;
phead->next->prev = newnode;
phead->next = newnode;
newnode->prev = phead;
}
和单链表一样简洁。
头插时需要注意一下链接的时候要从后面到前面,不然就找不到头插前的结点,除非你把它提前保存下来。
尾删数据
前面文章提到过说单链表不太适合尾插尾删,那双向链表非常适合尾插,看看它是否适合尾删。
void LTPopBack(LTNode* phead)
{
assert(phead);
assert(phead->next);
assert(phead->next!=phead);
LTNode* prev = phead->prev->prev;
LTNode* tail = phead->prev;
prev->next = phead;
phead->prev = prev;
free(tail);
}
接着测试一下这个代码是否适用于所有的情况

可以看到已经适合了所有情况。
总的来说,双向链表相比于单向链表有巨大优势。
1.不用根据是否要改变头结点的指针进行分类;
2.找尾结点和尾结点的前一个非常方便,相比于单链表效率高了不少。
头删数据
void LTPopFront(LTNode* phead)
{
assert(phead);
assert(phead->next);
assert(phead->next != phead);
LTNode* head = phead->next;
LTNode* next = phead->next->next;
phead->next = next;
next->prev = phead;
free(head);
}
头插还是跟单链表一样简洁。
注意,不要嫌多定义一个变量浪费或者麻烦,这样可以避免犯一些错误。
链表查找数据
LTNode* LTFind(LTNode* phead,LTDataType x)
{
LTNode* cur = phead->next;
while (cur != phead)
{
if (cur->data == x)
return cur;
cur = cur->next;
}
return NULL;
}
在pos位置前面插入数据
void LTInsert(LTNode* pos, LTDataType x)
{
assert(pos);
LTNode* newnode = BuyLTNode(x);
LTNode* posprev = pos->prev;
newnode->next = pos;
pos->prev = newnode;
posprev->next = newnode;
newnode->prev = pos;
}
与单链表相比,知道一个结点的地址之后可以直接找到前面一个结点的指针,而单链表需要遍历一遍链表。
并且同样不需要分类。
删除pos位置的数据
void LTErase(LTNode* pos)
{
assert(pos);
LTNode* posprev = pos->prev;
LTNode* posnext = pos->next;
posprev->next = posnext;
posnext->prev = posprev;
}
同样不需要分类
与单向链表相比,双向链表很好的解决了找到pos位置前一个结点时间复杂度o(N)的问题。
写完上面的两个函数,请问能否在十分钟写完一个链表?
其实我们可以把先写Insert函数和Erase函数,然后基本的增删查改都可以用这两个函数复用。
链表销毁
void LTDestory(LTNode* phead)
{
LTNode* cur = phead->next;
while (cur != phead)
{
LTNode* del = cur;
cur = cur->next;
free(del);
}
free(phead);
}
注意最后没必要写phead=NULL;因为形参的改变不会涉及实参的改变。
需要在函数外部来修改。
最后总结
细数一下与单链表相比有哪些优势?
1. 找尾结点不用遍历一次链表。
2. 不用考虑要不要改变头结点的指针进行分类,因为有哨兵卫的作用,完全不用改变头节点的指针。
3. 知道其中一个结点的指针时,不用遍历一次链表可以直接拿找到前一个结点。
可以说单链表只适合头插和头删除,不适合尾插尾删,但是这个链表结构都适合。