《machine learning in action》机器学习 算法学习笔记 支持向量机(Support Vector Machine)
支持向量机(Support Vector Machine)
数理证明
前置知识:拉格朗日数乘法、对偶问题、核技巧
拉格朗日数乘法
针对的是约束优化问题:
例题:
已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值__。
解:
引入参数 λ \lambda λ 构造新函数L: x + 2 y + λ ( x + 2 y + 2 x y − 8 ) x+2y+\lambda(x+2y+2xy-8) x+2y+λ(x+2y+2xy−8)
分别对x,y, λ \lambda λ求偏导:
L x = 1 + λ ( 1 + 2 y ) = 0 L y = 2 + λ ( 2 + 2 x ) = 0 L λ = x + 2 y + 2 x y − 8 = 0 L_x = 1+\lambda(1+2y)=0\\ L_y = 2+\lambda(2+2x)=0\\ \ \ \ \ \ \ L_\lambda = x+2y+2xy-8=0\\ Lx=1+λ(1+2y)=0Ly=2+λ(2+2x)=0 Lλ=x+2y+2xy−8=0
三个方程三个未知数,可以求得x=2,y=1。
即当x=2,y=1时x+2y的 最小值为4。
对偶问题
用于对优化问题的转换
例如:maxmin -> minmax
默认约束优化问题是弱对偶关系,当满足KNN条件时,具有强对偶关系,即二者等价。
核技巧
用于对高维特征的扩展,当样本数或超平面维数过大时,可以利用核技巧优化,将问题转化为有限维问题。
Machine Learning action
本章学习的是支持向量机中最流行的一种实现–序列最小优化(Sequential Minimal Optimization)算法。
优点:泛化错误率低,计算开销不大,结果容易理解
缺点:对参数调节和和函数的选择敏感,原始分类器不加修改仅适用于处理二分类问题。
适用数据类型:数值型和标称型数据
原理性部分
分割超平面集将不同类别的数据点分割的平面,支持向量机就是由这些分割超平面组成的分类器。
**支持向量(support vector)是指离分割超平面(separating byperplane)**最近的那些点,令支持向量的间隔最大化,就是构造支持向量机的优化目标
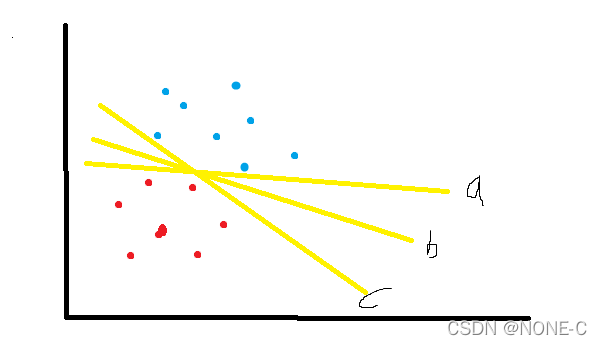
图中a,b,c都可以认为是一个分割超平面,显然,超分割平面b的鲁棒性即泛化能力要优于a,c。
如何建立数理模型来寻找到优质超分割平面?
那么就需要定义一个优化目标,即距离超分割面最近的那些的间隔最大化。
a r g m a x w , b { m i n ( w T ∗ x + b ) } arg\ max_{w,b}\ \{ min(w^T*x+b) \} arg maxw,b { min(wT∗x+b)}
其中w,b就是待优化的参数,假如直接求解该模型是十分困难的一件事,于是开始了一系列的模型转换,感兴趣的可以结合文章开头的视频以及西瓜书进一步学习,这里只将流程梳理一遍。
- 利用拉格朗朗日乘子法,得到拉格朗日方程组
- 将拉格朗日函数进行转换,转化为 a r g m i n m a x arg\ min max arg minmax问题
- 利用对偶问题的强对偶条件(KKT条件)将 a r g m i n m a x arg\ minmax arg minmax转化为 a r g m a x m i n arg\ maxmin arg maxmin问题
- 由于样本空间的非必线性可分,因此增加松弛变量
同时问题的参数也变为 α \alpha α,接下来便是对该问题进行求解
机器学习实战中使用的方法时SMO算法。
SMO算法伪代码:
创建一个alpha向量并将其初始化为0向量
当迭代次数小于最大迭代次数时(外循环):
对数据集中的每个数据向量(内循环):
如果该数据向量可以被优化:
随机选择另外一个数据向量
同时优化这两个向量
如果两个向量都不能被优化,退出内循环
如果所有向量都没有被优化,增加迭代数目,继续下一次循环
实际上SMO算法是一个较为有效的贪心算法。
code
'''
Created on Nov 4, 2010
Chapter 5 source file for Machine Learing in Action
@author: Peter
'''
from numpy import *
from time import sleep
def loadDataSet(fileName):
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat, labelMat
def selectJrand(i, m):
j = i # we want to select any J not equal to i
while (j == i):
j = int(random.uniform(0, m))
return j
def clipAlpha(aj, H, L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
dataMatrix = mat(dataMatIn)
labelMat = mat(classLabels).transpose()
b = 0
m, n = shape(dataMatrix)
alphas = mat(zeros((m, 1)))
iter = 0
while (iter < maxIter):
alphaPairsChanged = 0
for i in range(m):
fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
Ei = fXi - float(labelMat[i]) # if checks if an example violates KKT conditions
if ((labelMat[i] * Ei < -toler) and