基于Excel的QR二维码生成工具——原理及算法详解（之四）

在上一篇文章以及相关的两篇文章中，我们探讨了QR二维矩阵码生成过程中最关键的部分：里德所罗门纠错码（RS码）的生成原理及生成算法，不但涵盖了RS码的计算部分，同时还讨论了生成多项式、以及伽罗华域的相关理论，同时给出了Excel工作表函数的算法以及VBA算法代码。搞定了RS纠错码的计算，可以说QR码的生成工作就完成了大半了，因为剩余的部分都可以从QR Specification中得到很详尽的解释和示例。

从这篇文章开始，我们将按照顺序逐一讨论QR二维码生成过程中的各大步骤：

1. 数据编码——讨论不同的数据码字类型，以及一种Excel工作表函数算法生成数据编码
2. 数据编码——讨论混合数据码字的生成，并给出一种能够进行混合编码的VBA算法
3. 版本及格式数据——使用BCH纠错码计算版本及掩码纠错码
4. 二维码填充——二维码的填充方式，讨论VBA填充算法1：寻址法
5. 二维码填充——讨论VBA填充算法2：逐列法

因此，从本文开始，我将用五篇文章来逐一讨论上面的内容，本文的主要目的将讨论QR码的数据编码。

从QR标准文件中可以知道，标准的QR二维码是一个类似于下图的图形（另外还有一种模式的“MicroQR”并不在本文探讨范围内）：

在这样一个由深浅两色组成的正方形位图区域内，除了部分预留区域被用来填充固定的功能性图形以外，剩下的区域就是数据区域，所有的数据在被编码、再添加纠错码并分组乱序后，从最右下角开始，按照特定的顺序填充整个数据区域。最后覆盖上掩码，就成了最终的二维码图形。下图画出了所有的功能性图形和数据区域：

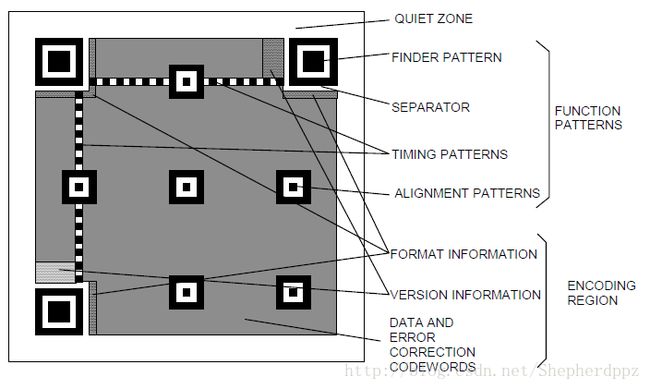
* 上图来自于ISO18004-2006
另外QR二维码有40个版本，版本数越大，码形尺寸也就越大，同时容纳的数据量也就越多。具体的图形信息大家可以参考标准文件，在此不再赘述。我们关注的是如何将数据编码。

国际标准的QR码有几种通用的编码形式，而中文汉字是在QR码的国标中规定了具体的编码形式。之所以QR码有多种不同的编码方式，主要目的是为了缩短编码的长度，从而增加二维码的容量。同时，为了实现混合编码，QR规范中也详尽规定了编码的具体结构：

字符编码段	模式指示符	字符计数指示符	数据位流	终止符
第一段	0010	000000101	00111001010000101110010
第二段	11010001	00000010	0101101010101000001011110
终止符				0000

上表显示了一条典型的完整数据编码码流，可以看出这条编码码流由两段组成，第一段是“字母数字”模式的编码，字符数量为5个字符，而第二段为“中国汉字”模式的编码，字符的数量为2个字符，两段编码分别以相应的模式指示符打头，继而连接字符计数指示符，最后跟上数据编码码流。当所有的编码段全部结束后，最后跟上“0000”终止符代表编码码字的结束。不过这里需要注意的是，终止符在解码的过程中并不起作用，只是用来填充数据位以保证整个码流能够正好分成8位字节的，因此可以被截短，也可以接续更多的“0”以补充到足够的位数。下面，就以一个简单的例子来解释Excel工作表函数的编码过程：

例如，现在需要将字符串“ABC23”编码，编码模式为字母数字，QR的版本为1-M。针对这样的编码，在Excel中我采用的方法是使用字符串和0~255的十进制数同时作为编码的输出，含有“0”或者“1”的字符串用来进行二维码的填充，使用Mid函数来取出相应的“0/1”值，而0~255的十进制数则被用来计算RS纠错码（计算RS纠错码的算法已经在前面两篇文章中解释过了）
因此，在Excel中，上述例子的编码过程如下：
1. 将字符串两两分组，放入一列单元格中，很容易通过Mid函数实现：“AB”，“C2”， “3”
2. 将分组后的字符分别编码，通过Vlookup函数从编码表中查找字符的编码值，并根据QR规范计算编码，同时转化为11位或6位0/1字符串：

• “AB” -> 10*45+11 = 461 -> “00111001101”
• “C2” -> 12*45+2 = 542 -> “01000011110”

• “3” -> 3 ->”000011” 3

  1. 在生成的字符串前面加上模式指示符和字数指示符（均为字符串形式，使用”&”连接，或使用Concaternate函数），同时，由于数据码流的长度不能被8整除，后面需要添加三个“0”以补足：

模式指示符	字数指示符	数据编码	终止符	补位符
0010	000000101	00111001101010…0011	0000	000

4. 再将字符编码分成8位一组，使用Mid函数，=MID(“数据码流”,i*8-7,8),其中“i”为数据码的组数

第1组	第2组	第3组	第4组	第5组	第6组
00100000	00101001	11001101	01000011	11000001	10000000
32	41	205	57	193	128

5. 由于编码用于填充1-M版本的QR码，这个版本的码字可以容纳128个bit，而数据编码长度不够，因此后面还需要添加上填充字符（236和17所代表的二进制数反复重复直到填满整个QR）。这样，整个数据编码就完成了：

组1	组2	组3	组4	组5	组6	组7	组8	组9	组10	组11	组12	组13	组14	组15	组16
32	41	205	57	193	128	236	17	236	17	236	17	236	17	236	17

完成上述编码后，就可以应用前面文章所讨论的RS纠错码生成算法计算码流的纠错码，通过QR规范可以查到，1-M版本的QR码所对应的RS纠错码为 RS(26,16)  也就是10个纠错码，根据QR规范中给出的生成多项式
可以直接计算纠错码，当然，小伙伴们也可以自己计算标准生成多项式，并用来计算纠错码，这样可以得出一个完全不同的纠错码，但是，两个纠错码都可以被正常填充并纠错：

g(x)	EC1	EC2	EC3	EC4	EC5	EC6	EC7	EC8	EC9	EC10
QR规范	73	134	125	49	139	166	29	86	171	126
标准计算	218	105	252	33	14	171	71	200	199	184

根据上面的例子，可以很容易构造一张计算工作表，将字符串转化为数据码流和字符串，如下图：

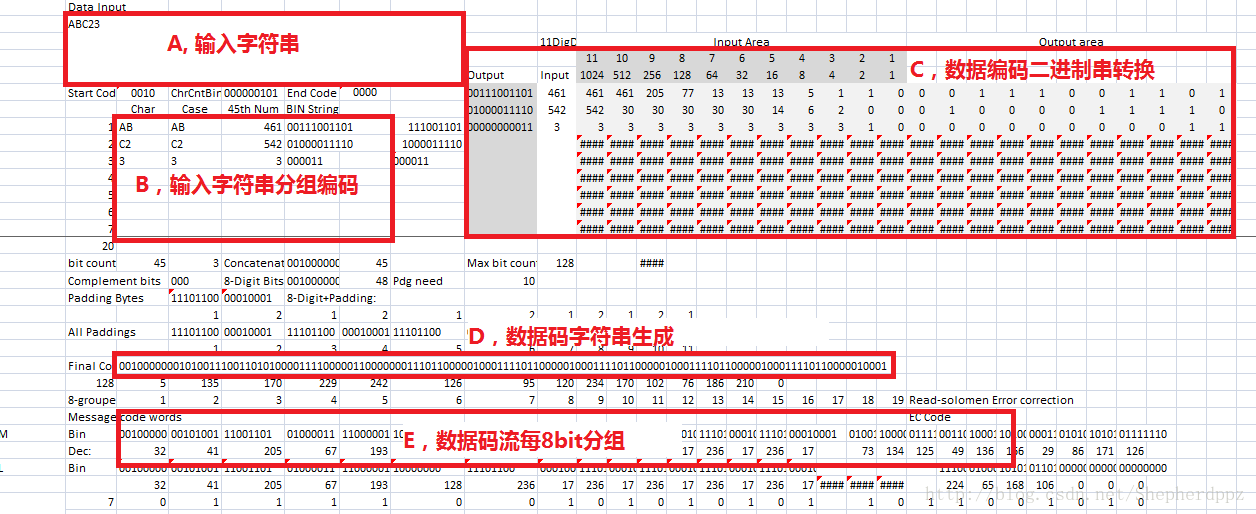
中文汉字和8位字节编码的构造方式与字母数字模式类似，不同的是8位字节模式直接使用字符的ASCII码作为字符编码，使用上简单一些，而中文汉字的编码如下：
1. 将每一个中文汉字编码为GB2312双字节编码（两个0~255之间的数字，QR规范上使用十六进制数&H0~&HFF，这里统一使用十进制），记为 x 1   与 x 2  
2. 令最终编码为 y  ，如果第一个汉字的编码在161到170之间时：

y=(x 1 −161)∗96+(x 2 −161) 

,再将 y  编码为13位二进制数编码串
3. 如果第一个汉字的编码在176到250之间时，

y=(x 1 −166)∗96+(x 2 −161) 

,再将$y$编码为13位二进制数编码串

在此做一些补充：
在上面的例子中，将十进制编码转为二进制并转为字符串时，如果使用工作表函数，由于Dec2Bin函数最多只能转化512以内的十进制整数，超过512只能得到“#NUM!”的结果，因此需要使用下面的表格来进行十进制到二进制的转换（这个转换表没有位数的限制，当然，使用VBA写自定义函数也是可以的）

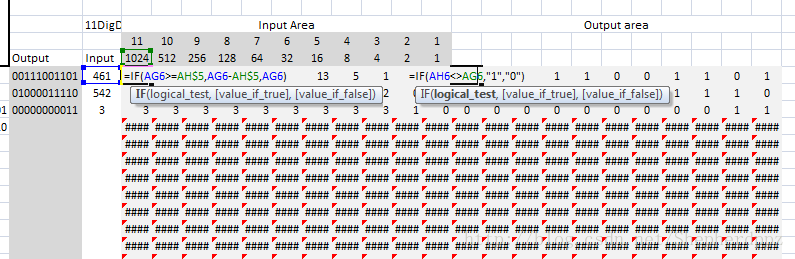
如上图所示，在左边的Input area中，逐位判断输入数值是否大于表头的二进制数，是则表示该二进制数位为1，否则为0。若该位为1，则用输入数减去表头二进制数作为新的输入数，进行下一位计算，一直到数字为0为止。右边部分则是简单的条件判断，判断该二进制数位为0还是1.然后将所有二进制位连接起来做成字符串，就成为最左列的输出字符串。

上面的计算表在VBA中可以写成工作表函数调用，效果也是一样的：

Private Function Sdec2bin(n As Long, l As Long) As String
Dim char As String * 1, str As String
Dim i As Long
    For i = l To 1 Step -1
        char = IIf((n And 2 ^ i) = 0, "0", "1")
        str = str + char
    Next
    Sdec2bin = str
End Function

至此，我们已经讨论了QR码的数据编码的具体实现过程，数据被编码后首先被转换为“0/1”字符串并被连接起来，每8bit分组后再被转换为一组0~255的数值数据以便计算RS纠错码，计算完成后再次被转化为字符串形式，以便未来被用来进行二维码单元格区域的填充。但是，通过工作表函数来进行数据编码有一个极大的弱点，那就是很难实现不同模式的混合编码，而且公式实现比较复杂。在下一篇文章中，我们还将继续讨论
数据编码的问题，并讨论一个VBA算法，用来解决混合编码的问题