排序算法——堆排序

目录

1️⃣概念回顾

二叉树

完全二叉树

大根堆

小根堆

 2️⃣堆排序

 基本介绍：

算法思想：

实例：

思路步骤：

代码实现：

算法性能分析：

---

学习堆排序之前，先回顾以下概念：

1️⃣概念回顾

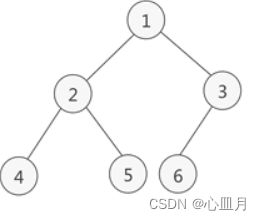
二叉树：

二叉树是指树中节点的度不大于2的有序树。

（节点的度：一个节点拥有子树的数目称为节点的度）

（分枝结点： 度不为0的结点）

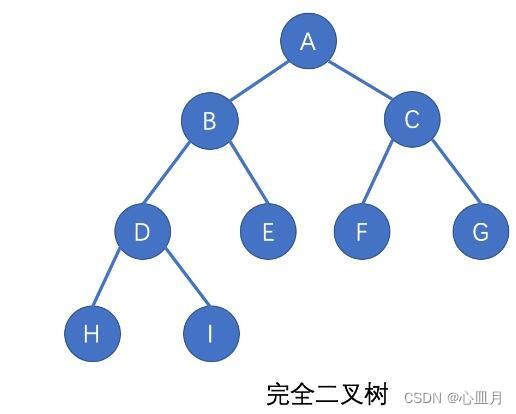
完全二叉树：

完全二叉树是指：二叉树上每一层都是满的，或者最后一层没填满并且最后一层的叶子节点集中在树的左部。

例如：

（需要注意的是，满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。）

大根堆

每个结点的值都大于等于其左、右孩子的值。

 

小根堆

每个结点的值都小于等于其左、右孩子的值。

 2️⃣堆排序

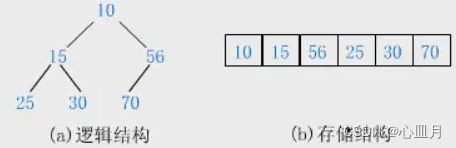
堆排序使用的是二叉堆的概念，二叉堆是一颗完全二叉树。

思考：从逻辑层面，如何将需要排序的数组转换成完全二叉树的形式？

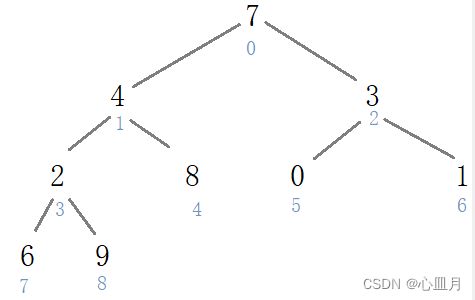
根据观察规律，可以得出节点与其左右孩子下标之间的关系：

当前节点下标	左孩子下标	右孩子下标
0	1	2
1	3	4
2	5	6
3	7	8
i	2*i+1	2*i+2

 基本介绍：

堆排序是利用堆这种数据结构所设计的一种排序算法。

堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。

升序采用大顶堆，降序采用小顶堆。

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

算法思想：

1、将无序序列构建成一个堆，根据升序降序需求选择大根堆或小根堆

2、将调整后的堆顶元素与末尾元素进行交换，将最大元素“沉”到数组末端。

3、将剩下元素重新构造成一个堆，继续进行调整，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

⭐将堆调整成大根堆，调整思路：

• 从最后一个非叶子节点开始

寻找最后一个非叶子节点：不一定有右孩子，所以直接用左孩子节点来求：2*i+1=arr.length-1,则i=(arr.length-1-1)/2 

• 选择左、右孩子中的较大值
• 将较大值与其父节点相比较，将最大者调整为父节点
• 从下至上，从右至左，依次进行调整

实例：

对数组[7,4,3,2,8,0,1,6,9]进行堆排序，升序排序。

思路步骤：

1、先将数组构建成一个堆

 

2、调整为大根堆的形式：

找最后一个非叶子节点：(arr.length-1-1)/2=7/2=3，下标为3 的节点为2

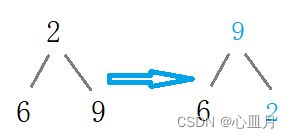
故先将[2,6,9]调整为大根堆形式：

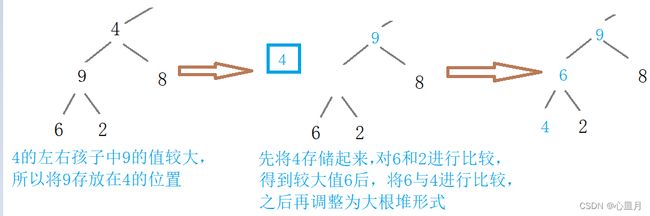
 3、接下来该调整节点3 ，发现已经是大根堆形式；所以，开始调节节点4。

 

‼

需要注意的是：

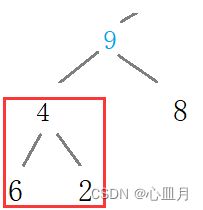
4不要直接放入9的位置，若直接放入会导致[4,6,2]结构混乱，如图：

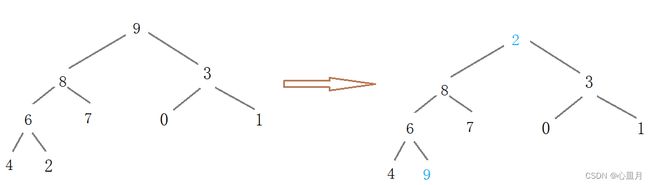
 4、接下来调整堆顶元素

 5、将调整完成之后的堆顶元素与末尾元素进行交换，对剩余元素重复以上步骤，直至整个序列有序。

 每一轮完成之后，都会将本轮中最大的元素“沉”到数组末端。可以看到在构建大顶堆的过程中，元素的个数逐渐减少，最后就会得到一个有序序列.

代码实现：

public class HeapSort {
    //调整为大根堆的过程：
    public static void adjust(int[] arr,int begin,int end) {
        //①保存begin位置的值
        int temp = arr[begin];
        //②挑选左右孩子中的较大值
        for (int i = 2 * begin + 1;i <= end;i = 2 * i + 1) {
            if (i + 1 <= end && arr[i] < arr[i + 1]) {
                 i= i + 1;//用i保存左右孩子值较大值的【下标】
            }
            //③较大值与begin位置的值比较
            if (arr[i] > temp ) {
                arr[begin] = arr[i];
                begin = i;//交换之后，更新begin的值
            }else {
                break;
            }
        }
        //越界后，最终再把temp值赋给begin位置的值
        arr[begin] = temp;

    }
    public static void heapSort(int[] arr) {
        //1.将堆调整成大根堆的形式(从最后一个非叶子节点开始)
        for (int i = (arr.length - 1 - 1) / 2; i >= 0; i--) {
            adjust(arr,i,arr.length - 1);
        }
        //2.交换堆顶元素和“相对最后”的元素
        for (int i = 0;i < arr.length;i++) {
            int temp = arr[0];
            arr[0] = arr[arr.length - 1 - i];//有i个元素就交换i趟，每一趟走完后定一个元素
            arr[arr.length - 1 - i] = temp;
            adjust(arr,0,arr.length -1 - 1 - i);
        }

    }

    public static void main(String[] args) {
        int[] arr = {7,4,3,2,8,0,1,6,9};
        heapSort(arr);
        System.out.println("排序后为:" + Arrays.toString(arr));
    }
}

运行结果：

算法性能分析：

（1）平均时间复杂度：O（)

(2)空间复杂度： O(1)

(3)稳定性： 不稳定