leetcode 每日一题复盘(11.20~11.26)

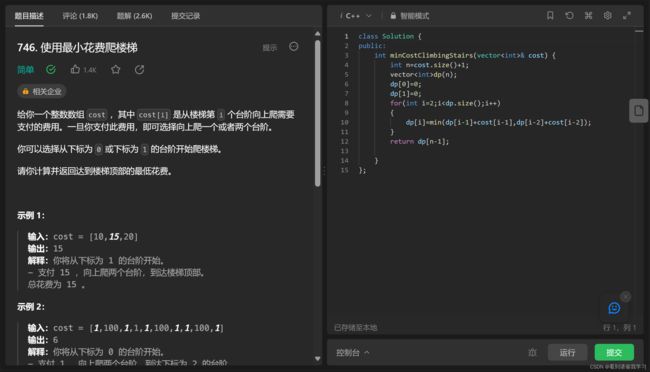
leetcode 746 使用最小花费爬楼梯

虽然是简单题但还是要说一下,感觉做题的思路还是不够清晰,好的是知道状态是最低花费,知道围绕所求的目标进行展开,倒推出递推公式

一开始写的递推公式是dp[i]=dp[i-1]+min(cost[i-2],cost[i-1]),写出了一个类似贪心算法的东西,归根结底还是对dp状态的认识不过,不清楚i代表什么,dp代表什么

实际上dp代表的是到达某一层的最低花费,而i则是层数,上面就是对i的代表不明确导致的,正确的推导公式应该是dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]),选择从i-1层和i-2层到达i层两者的最小值

其他的没什么好讲的,也就是题目表达的不是很好,有点难理解,需要跨越数组的最后一个元素(下标为n)才是到达楼顶而不是到达最后一个元素(下标n-1) 

因此我们最后取dp的下标是n,也就是数组cost的长度(最后一个元素的下一位)

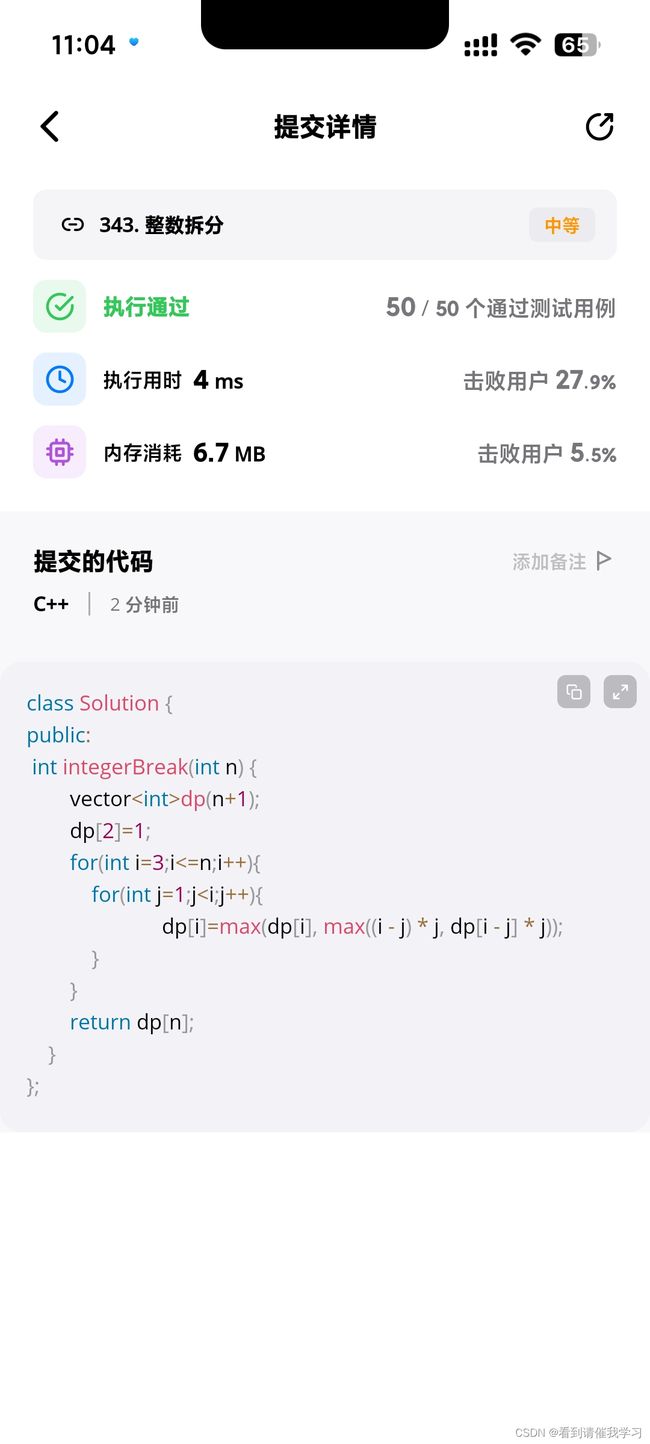
leetcode 343 整数拆分

一直想不出来dp数组怎么递推，这也是这道题的难点，后来想用数学推导的方法解决(因为知道两个数相等时乘积最大)，但是最后也没解决出来

这道题为什么难呢?因为有多种状态，你可以分成2个数相乘也可以分成3，4个数相乘，状态很多就难以确定哪个是最大的，dp的前一个状态就难以确定，就不要说求dp的状态了

dp递推公式难以确定，如果我们要求dp[n]，一般会用到dp[n-1]，dp[n-1]怎么样才能变成dp[n]呢，一开始我们很难想清楚

n是我们要拆分的数字，如何进行拆分:可以分成拆分成两个数字和两个数字以上两种

分成两个数字的，dp[n]＝（n-j）*j，j代表n分出来的数字

分成两个数字以上的，dp[n]＝dp[n-j]*j，dp[n-j]代表n-j的拆分数字的乘积组合

因为我们要求dp[n]，我们需要从dp[3]开始递推（0，1，2只有一种情况，已经确定值大小），因此设i＝3开始遍历构造dp数组，设j为i分出来的数字，因此j需要小于i

那么回到递推公式，递推公式应该怎么写呢，dp[n]＝max（dp[n-j]*j，（n-j）*j）?，这样想就太简单了，我们还需要在max外层再套一层max用来keep住最大值，而不是简单的比较j这个情况两者的最大值

---

如果是第一次做这题，感觉还是不好做的（也许是我笨），面对复杂情况，无法简单得出递推公式时，可以尝试分类简化，抓住本质（所乘的数都是从n拆分出来的）

leetcode 96 不同的二叉搜索树

看题目好像挺简单,但是实际上做起来的时候让人摸不着头脑,dp的上一个状态怎么和下一个状态联系起来呢,也是这一题的难点

首先需要明确的是dp代表的状态是n个节点的二叉搜索树的数量

我们很容易可以得知dp[3]=5,也就是3个节点时二叉树有5种,那么怎么求dp[4]呢,怎么将dp[4]和dp[3]联系起来呢,答案是无法直接联系的,现在的题目情况复杂,已经无法直接从上一个状态得出下一个状态了,必须结合之前所有的状态综合考虑

对于复杂情况,我们可以进行分类,将以哪个数字为根作为依据进行分类,那么dp[4]可以分成4类分别是1,2,3,4

1为根时,其右子树有三个元素,左子树没有元素即dp[3]*dp[0]

2为根时,其右子树有两个元素,左子树有一个元素即dp[2]*dp[1]

3为根时,其右子树有一个元素,左子树有两个元素即dp[1]*dp[2]

4为根时,其右子树没有元素,左子树有三个元素即dp[0]*dp[3]

几种情况加起来就是dp[4]

有些同学可能会疑惑为什么是乘而不是加呢,因为当右子树里有多种情况,左子树里也有多种情况时我们需要用乘法才能将每一种情况都完全列出来

明白了上面这个例子就可以写递推公式啦,用两层for循环遍历,一层确定要求的dp一层确定根的数字的分布情况

dp[i]+=dp[j-1]*dp[i-j]//j-1表示j为根时的左子树的数字数量(j-1表示除去根之外比根小的),i-j表示j为根时右子树的数字数量,i也就是一共有多少个数字

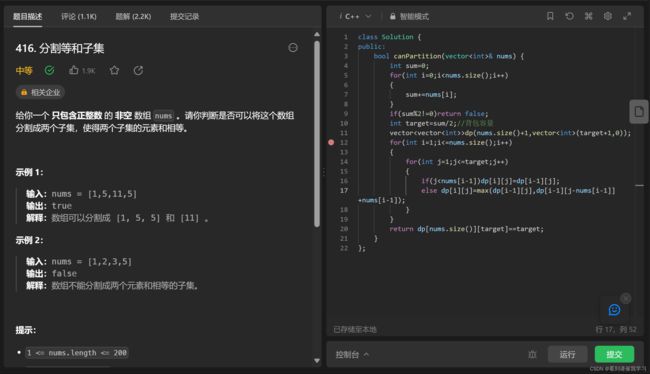
leetcode 416 分割等和子集

01背包问题,一个字:难 刚学背包问题先写一个二维数组的版本理解一下先

第一步确定dp数组:把target(数组和一半)作为背包容量,作为j;把数组中的元素作为物品的大小,同样也是物品的值,作为i;dp数组表示数组元素的和

第二部确定递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - nums[i-1]] + nums[i-1]);推导过程就不细说,也就是分成两类,放i和不放i的,放i的时候还要用max比较取最大值

也许有的同学会疑惑为什么不是dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);呢?因为这里j=0时是表示容量为0,i=0时表示物品大小为零,所以我们的数组的第0行和第0列都是不使用的,我们初始化的数组是target+1,size+1把第0行列空出来
而有的数组是使用第0行,列的所以递推公式中的下标有所不同,需要因题而异

这里为啥是nums[i-1]呢,不是把下标为i的元素加上吗?一开始我也很疑惑,答案是因为我们初始化dp数组的时候长度是要比nums大1的,因此直接用i的话会造成偏移,所以我们需要i-1表示正确的下标,当然我们也可以自己检查一下,把i代进去看看就会发现数组越界了

一般遍历物品数组的时候判断条件是不会等于的,都是因为数组初始化造成的变化

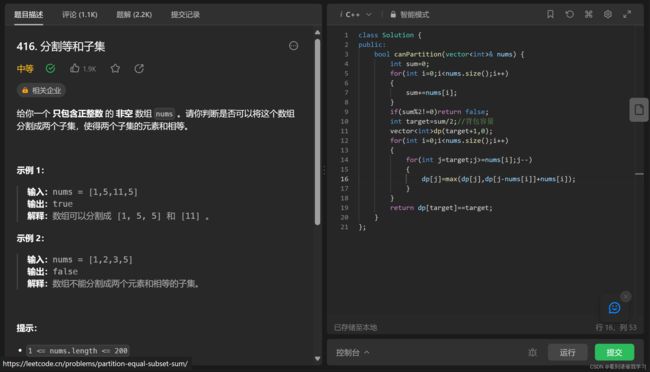
这里补回一个一维数组的版本,一维数组写起来确实简洁,效率又高,熟悉了之后确实好用