数据结构与算法——29. 图（Graph）的概念及应用

一、图（Graph）的概念

图Graph是比树更为一般的结构，也是由节点和边构成。而实际上树是一种具有特殊性质的图。

图可以用来表示现实世界中很多事物：道路交通系统、航班线路、互联网连接、或者是大学中课程的先修次序。

一旦我们对图相关问题进行了准确的描述，就可以采用处理图的标准算法来解决那些看起来很艰深的问题。

对于人来说，人脑的识别模式能够轻而易举地判断地图中不同地点的相互关联；但如果用图来表示地图，就可以解决很多地图专家才能解决的问题，甚至远远超越；

互联网是由成千上万的计算机所连接起来的复杂网络，也可以通过图算法来确定计算机之间达成通讯的最短、最快或者最有效的路径。

1. 图的相关术语

• 顶点（Vertex，也称“节点node”）：
  是图的基本组成部分，定点具有名称标识key，也可以携带数据项payload。

• 边 （Edge，也称“弧Arc”）：
  作为2个顶点之间关系的表示，边连接两个顶点；边可以是有向的或者无向的，相应的图称做“有向图”和“无向图”。

• 权重（Weight）：
  为了表达从一个顶点到另一个顶点的“代价”，可以给边赋权；

  例如公交网络中两个站点之间的“距离”、“通行时间”和“票价”都可以作为权重。

• 路径（Path）：
  图中的路径，是由边依次链接起来的顶点序列；无权路径的长度为边的数量；带权路径的长度为所有边权重的和；

  如下图的一条路径(v3,v4,v0,v1)：

• 圈（Cycle）：
  圈或环是首尾顶点相同的路径，如上图中（V5,V2,V3,V5）。

  如果有向图中不存在任何圈，则称为“有向无圈图 directed acyclic graph：DAG”。如果一个问题能表示成DAG，那么就可以用图算法很好地解决。我们之前学的树结构，其实就是一种DAG。

2. 图的定义

一个图G可以定义为G=(V, E)。其中V是顶点的集合，E是边的集合，E中的每条
边e=(v, w)，v和w都是V中的顶点；

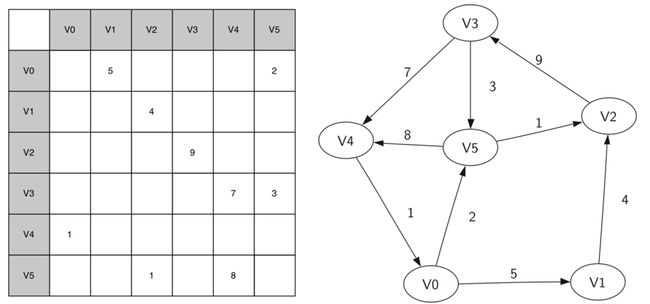
如果是赋权图（边带有权重的图，也叫带权图），则可以在e中添加权重分量子图：V和E的子集。比如下面的有向赋权图：

$$V=\{V0,V1,V2,V3,V4,V5\}$$

$$E=\{(v0,v1,5),(v1,v2,4),(v2,v3,9),(v3,v4,7),(v4,v0,1),(v0,v5,2),(v5,v4,8),(v3,v5,3),(v5,v2,1)\}$$

二、图抽象数据类型（ADT Graph）

ADT Graph的实现方法有两种主要形式：

1. 邻接矩阵（adjacency matrix）
2. 邻接表（adjacency list）

两种方法各有优劣，需要在不同应用中加以选择。

1. 邻接矩阵实现图

矩阵的每行和每列都代表图中的顶点，如果两个顶点之间有边相连，设定行列值。无权边则将矩阵分量标注为1（代表有边），或者0（代表无边，也可以不写）；带权边则将权重保存为矩阵分量值。

比如，下面的邻接矩阵和它所表示的赋权图：

邻接矩阵实现法的优点是简单，可以很容易得到顶点是如何相连。

但如果图中的边数很少则效率低下，成为**“稀疏sparse”矩阵**。而大多数问题所对应的图都是稀疏的，边远远少于$|V{|}^2$这个量级。

2. 邻接列表实现图

邻接列表可以为稀疏图提供更高效的实现方案：维护一个包含所有顶点的主列表（master list），主列表中的每个顶点，再关联一个与自身有边连接的所有顶点的列表。

还是上面的赋权图，其邻接列表的表示如下：

邻接列表法的存储空间紧凑高效，很容易获得顶点所连接的所有顶点，以及连接边的信息。

3. python代码实现

class Vertex:
    """顶点类"""
    def __init__(self,key):
        self.id = key # 顶点的key
        self.connectedTo = {}  # 与自身有边连接的所有顶点的列表

    def addNeighbor(self,nbr,weight=0):  # nbr是顶点对象的key
        """向邻接表添加一个当前顶点连接到另一顶点的键值对"""
        self.connectedTo[nbr] = weight

    def __str__(self):
        """print方法的输出内容""" 
        return str(self.id) + ' connectedTo: ' + str([x.id for x in self.connectedTo])

    def getConnections(self):
        """返回邻接表中的所有顶点"""
        return self.connectedTo.keys()

    def getId(self):
        """返回当前顶点的key"""
        return self.id

    def getWeight(self,nbr):
        """返回当前顶点到目标顶点nbr的边的权重"""
        return self.connectedTo[nbr]


class Graph:
    """图类"""
    def __init__(self):
        self.vertList = {}  # 顶点集合
        self.numVertices = 0  # 顶点数量

    def addVertex(self,key):
        """添加顶点"""
        self.numVertices = self.numVertices + 1
        newVertex = Vertex(key)
        self.vertList[key] = newVertex
        return newVertex

    def getVertex(self,n):
        """获取指定顶点"""
        if n in self.vertList:
            return self.vertList[n]
        else:
            return None

    def __contains__(self,n):
        """实现in操作"""
        return n in self.vertList

    def addEdge(self,f,t,weight=0):
        """添加边"""
        if f not in self.vertList:
            nv = self.addVertex(f)
        if t not in self.vertList:
            nv = self.addVertex(t)
        self.vertList[f].addNeighbor(self.vertList[t], weight)

    def getVertices(self):
        """获取所有顶点"""
        return self.vertList.keys()

    def __iter__(self):
        """实现迭代"""
        return iter(self.vertList.values())

三、图的应用：词梯问题

由《爱丽丝漫游奇境》的作者Lewis Carroll在1878年所发明的单词游戏：从一个单词演变到另一个单词，其中的过程可以经过多个中间单词，要求是相邻两个单词之间差异只能是1个字母。

如FOOL变SAGE：FOOL >> POOL >> POLL >> POLE >> PALE >> SALE >> SAGE

我们的目标是找到最短的单词变换序列！采用图来解决这个问题的步骤如下：

1. 将可能的单词之间的演变关系表达为图；
2. 采用“广度优先搜索（BFS）”，来搜寻从开始单词到结束单词之间的所有有效路径；
3. 选择其中最快到达目标单词的路径。

1. 构建单词关系图

首先是如何将大量的单词集放到图中？
将单词作为顶点的标识Key。如果两个单词之间仅相差1个字母，就在它们之
间设一条边。

下图是从FOOL到SAGE的词梯解，所用的图是无向图，边没有权重。FOOL到SAGE的每条路径都是一个解。

单词关系图可以通过不同的算法来构建，首先是将所有单词作为顶点加入图中，再设法建立顶点之间的边。

建立边的最直接算法，是对每个顶点（单词），与其它所有单词进行比较，如果相差仅1个字母，则建立一条边。时间复杂度是$O(n^2)$，对于所有4个字母的5110个单词，需要超过2600万次比较。

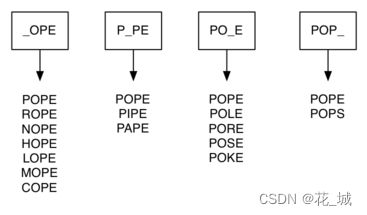
改进的算法是创建大量的“桶”， 每个桶可以存放若干单词。桶标记是去掉1个字母，使用通配符“_”顶替去掉的的字母。所有单词就位后，再在同一个桶的单词之间建立边即可。

2. python代码实现

我们采用“桶”的方法连接顶点：

from pythonds.graphs import Graph

def buildGraph(wordFile):
    d = {}
    g = Graph()
    wfile = open(wordFile,'r')
    # 读取所有单词
    for line in wfile:
        word = line[:-1]
        # 将单词放入桶中
        for i in range(len(word)):
            bucket = word[:i] + '_' + word[i+1:]
            if bucket in d:
                d[bucket].append(word)
            else:
                d[bucket] = [word]
	# 同一个桶的单词建立边
    for bucket in d.keys():
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1,word2)
    return g

注意，如果采用邻接矩阵表示这个单词关系图，则需要2,600万个矩阵单元，单词关系图是一个非常稀疏的图。