多元统计分析 样本均值的假设检验例题

例一

大学生的素质高低要受各方面因素的影响，其中包括家庭环境与家庭教育（x1）、学校生活环境（x2）、学校周围环境（x3）和个人向上发展的心理动机（x4）等。从某大学在校学生中抽取了20人对以上因素在自己成长和发展过程中的影响程度给予评分（以9分制），数据如下表所示：

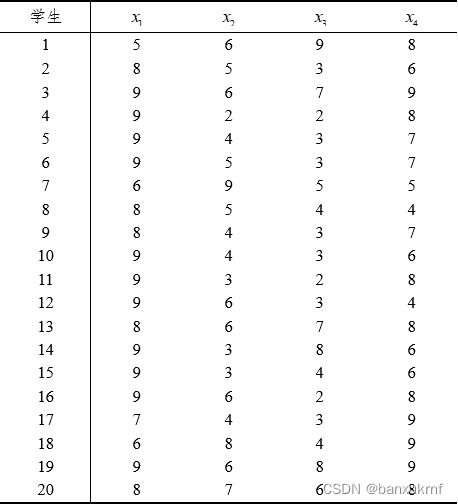
假定x=(x1,x2,x3,x4)’ 服从四元正态分布。试检验:$H_0$：μ = ${\mu }_0$=(7，5，4，8），$H_1$：μ ≠ ${\mu }_0$；（α=0.05）。

---

解：明显是单样本总体协方差未知，因此检验统计量为

T²=n( $\bar{X}$- ${\mu }_0$)' $S^{-1}$( $\bar{X}$- ${\mu }_0$)

部分代码如下：

df = data[['x1','x2','x3','x4']]

#总体均值
Mu = np.array([7,5,4,8])
#样本均值
xbar = df.mean()
print(xbar)
#样本协方差矩阵
S = df.cov()
print(S)
#S的逆矩阵
S1 = np.linalg.inv(S)
temp = np.dot(xbar-Mu,S1)
temp = np.dot(temp,xbar-Mu)
print("T²:")
tsquare = n*temp
print(tsquare)
print("F:")
F = tsquare*(n-p)/(p*(n-1))
print(F)
#单侧右分位点
print("a:")
a = f.isf(alpha,p,n-p)
print(a)

---

例二

测量30名初生到3周岁婴幼儿的身高（x1）和体重（x2）数据如下表所示，其中男女各15名。假定这两组都服从正态总体且协方差阵相等，试在显著性水平下检验男女婴幼儿的这两项指标是否有差异。

---

解：两个样本，总体协方差未知且相等，因此检验统计量为

T²=(nm/m+n)( $\bar{X}$- $\bar{Y}$)' $S_p^{-1}$( $\bar{X}$- $\bar{Y}$)

df1 = data1[['x1','x2']]
df2 = data2[['x1','x2']]

#两总体样本均值向量
Xbar=df1.mean()
Ybar= df2.mean() 
print(Xbar)
print(Ybar)

#两样本协方差矩阵
S1=df1.cov()
S2=df2.cov()
Sp=((n-1)*S1+(n-1)*S2)/(2*n-2)

#求出Sp的逆矩阵
S3=np.linalg.inv(Sp) 
temp=np.dot(Xbar-Ybar,S3)
temp=np.dot(temp, Xbar-Ybar)

print("T²:")
tsqure=n*temp/2.0 
print(tsqure)
print((2*n-p-1)*tsqure/(2*n-2)/p)

print("F:")
F=tsqure*(2*n-p-1)/(p*(2*n-2)) 
print(F)

print("a:")
a=f.isf(alpha, p, 2*n-p-1) 
print(a)

例三

在对1958-1967年美国制造业中垄断作用的经验检验中，阿瑟和赛尼卡(Asch and Seneca, 1976)调查了由45家消费资料生产企业和56家生产资料生产企业组成的样本，被调查指标有5个：①利润率——税后净利润与该时期股票持有者的股票数量之比的平均值；②产业集中度——四个大企业货运量的比率；③风险——关于趋势线的利润率的标准差；④企业规模——平均总资产的对数；⑤销售增长率——该时期销售收入的平均增长率。消费资料生产企业样本观测矩阵记为X，生产资料生产企业样本观测矩阵记为Y，由这两个样本观测矩阵计算得到两样本各自的均值向量和叉积矩阵，分别为：

$A_1$= ( 1694.310 2953.721 1977.249 − 584.067 24.815 2953.721 12204.726 4575.176 239.037 − 11.156 1977.249 4575.176 21876.185 − 480.041 3.514 − 584.067 239.037 − 480.041 69.256 − 0.791 24.815 − 11.156 3.514 − 0.791 0.088 ) \left(\begin{matrix}1694.310&2953.721&1977.249&-584.067&24.815\\2953.721&12204.726&4575.176&239.037&-11.156\\1977.249&4575.176&21876.185&-480.041&3.514\\-584.067&239.037&-480.041&69.256&-0.791\\24.815&-11.156&3.514&-0.791&0.088\\\end{matrix}\right) ​1694.3102953.7211977.249−584.06724.815​2953.72112204.7264575.176239.037−11.156​1977.2494575.17621876.185−480.0413.514​−584.067239.037−480.04169.256−0.791​24.815−11.1563.514−0.7910.088​ ​

$A_2$= ( 80074.285 10368.309 2355.126 227.307 43.657 10368.309 14916.958 5654.126 331.117 0.050 2355.886 5654.126 27725.247 417.979 1.352 227.307 331.117 417.979 100.822 − 0.285 43.657 0.050 1.352 − 0.285 0.165 ) \left(\begin{matrix}80074.285&10368.309&2355.126&227.307&43.657\\10368.309&14916.958&5654.126&331.117&0.050\\2355.886&5654.126&27725.247&417.979&1.352\\227.307&331.117&417.979&100.822&-0.285\\43.657&0.050&1.352&-0.285&0.165\\\end{matrix}\right) ​80074.28510368.3092355.886227.30743.657​10368.30914916.9585654.126331.1170.050​2355.1265654.12627725.247417.9791.352​227.307331.117417.979100.822−0.285​43.6570.0501.352−0.2850.165​ ​

试分析两类企业的相关指标向量均值是否相同。

---

解：这题和上一题是一样的，只不过把$S_1$和$S_2$换成了$A_1$和$A_2$

A = np.add(A1,A2)
A_1 = np.linalg.inv(A)

temp = np.dot(Xbar-Ybar,A_1)
temp = np.dot(temp,Xbar-Ybar)

tsquare = (n+m-2)*n*m*temp/(n+m)
print(tsquare)

F = (n+m-p-1)*tsquare/p/(n+m-2)
print(F)

a = f.isf(alpha,p,n+m-p-1)
print(a)
#F>a因此拒绝原假设

例四

在企业市场结构研究中，起关键作用的指标有市场份额X1，企业规模（资产净值总额的自然对数）X2，资本收益率X3，总收益增长率X4。为了研究市场结构的变动，夏菲尔德（Shepherd,1972）抽取了美国231个大型企业，调查了这些企业1960-1969年的资料。假设以前企业市场结构指标的均值向量为(20,7.5,10,2)’，而该次调查所得到的企业市场结构指标的均值向量(20.92,8.06,11.78,1.09)’和总体协方差矩阵。试问企业市场结构是否发生了变化？

---

解：单个总体，总体协方差已知

#总体均值
Mu = np.array([20,7.5,10,2])
#样本均值向量
xbar = np.array([20.92,8.06,11.78,1.09])
#总体协方差矩阵
sig = np.array([[0.26,0.08,1.639,0.156], [0.08,1.513,-0.222,-0.019],[1.639,-0.222,26.626,2.233],[0.156,-0.019,2.233,1.346]])
#求出S的逆矩阵
sig1 = np.linalg.inv(sig)

temp = np.dot(Mu-xbar,sig1) 
temp = np.dot(temp,Mu-xbar)

print("Z²:")
zspuare = n*temp
print(zspuare)

print("a:")
a = chi2.isf(alpha,p)
print(a)

例五

对20名健康女性的汗水进行测量和化验，X1 =排汗量，X2 =汗水中钠的含量，X3 =汗水中钾的含量，为了探索新的诊断技术，需要检验假设H0：μ′=（4，50，10）对H1：μ′≠（4，50，10），取显著性水平α=0.10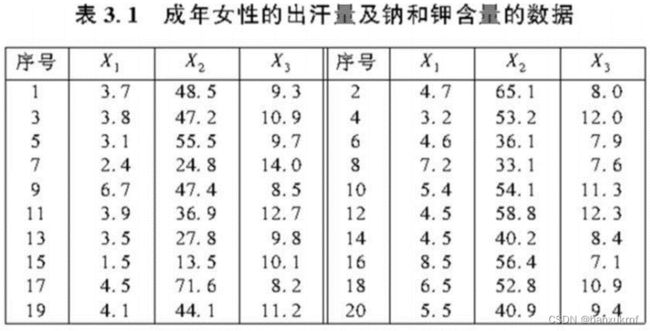

---

解：单个总体，总体协方差未知

df = data[['x1','x2','x3']]

Mu = np.array([4,50,10])
Xbar = df.mean()
S = df.cov()
S1 = np.linalg.inv(S)
temp = np.dot(Xbar-Mu,S1)
temp = np.dot(temp,Xbar-Mu)
print("T²:")
tsquare = n*temp
print(tsquare)
F = tsquare*(n-p)/(p*(n-1))
print("a:")
a = f.isf(alpha,p,n-p)
print(a)