数据结构——森林与并查集
并查集能解决连通性问题,如 A = B , B = C , C = D 能推导出 A = D
一. 连通性问题
二. Quick-find
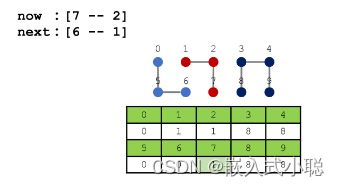
- 基于 染色 的思想,一开始所有点的颜色不同
- 连接两个点的操作,可以看成将 一种颜色 的点染成 另一种颜色
- 如果两个点颜色 一样,证明连通,否则不连通
- 这种方法叫做并查集的【Quick-Find算法】
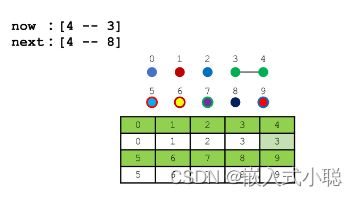
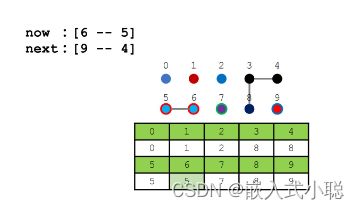
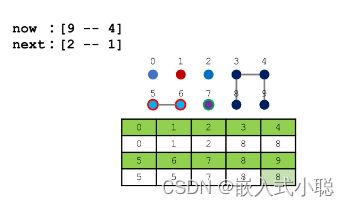
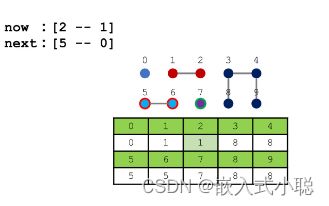
Quick-find 算法中修改点颜色的时间复杂度为 O(n) ,而判断连通关系的时间复杂度为 O(1),即判断数组中保存的值是否相同
next:[6 --- 1] 将6号点颜色改成1号点颜色
代码实现:
#include#include #define MAX_N 10000 int colour[MAX_N]; //初始化每个点的颜色为数组下标 void init(int n) { for (int i = 0; i <= n; i++) colour[i] = i; return ; } //查找某个点的颜色 //查找:O(1) int find(int a) { return colour[a]; } //合并两个集合(全部改成b集合颜色) /* 连通判断:O(1) 合并操作:O(n) */ bool merge(int a, int b, int n) { int aa = find(a), bb = find(b); if (aa == bb) return false; for (int i = 0; i <= n; i++) { if (colour[i] == aa) colour[i] = bb; } return true; } //打印 void output(int n) { int ret = 0; for (int i = 0; i <= n; i++) ret += printf("%d ", i); printf("\n"); for (int i = 0; i < ret; i++) printf("-"); printf("\n"); for (int i = 0; i <= n; i++) printf("%d ", colour[i]); printf("\n"); return ; } int main(int argc, char *argv[]) { int n, a, b; //n:(点的数量) a:(点a) b:(点b) scanf("%d", &n); init(n); //初始化每个点的颜色为数组下标 while (1) { scanf("%d%d", &a, &b); if ((a >= 0 && a <= n) && (b >= 0 && b <= n)) { if (merge(a, b, n)) printf("merge %d with %d : %d\n", a, b, merge(a, b, n)); } else break; output(n); } return 0; }
三. Quick-Union
问题思考:
quick-find算法的连通判断非常快,可是合并操作非常慢- 本质上问题中只是需要知道一个点与哪些点的颜色相同
- 而若干点的颜色可以通过间接指向同一个节点
- 合并操作时,实际上是将一棵树作为另一个棵树的子树
合并过程:
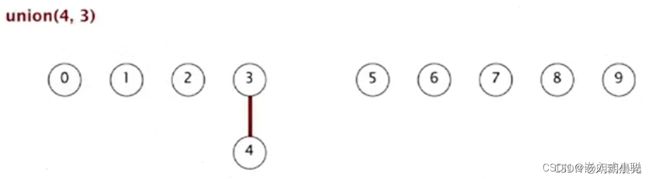
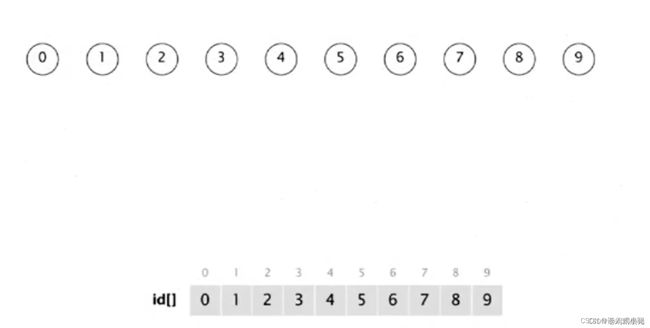
1、初始:每个点都是自己的根
2、union(4,3):4 的父亲变为 3
3、union(3,8):3 的父亲是 8
4、union(6,5): 6 的父亲是 5
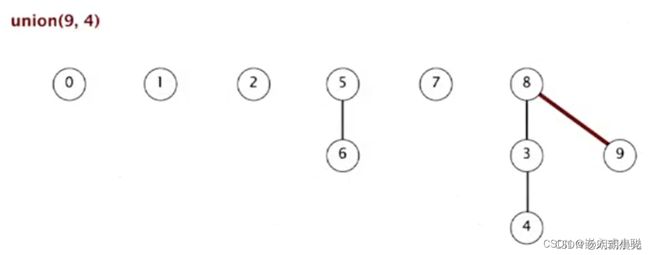
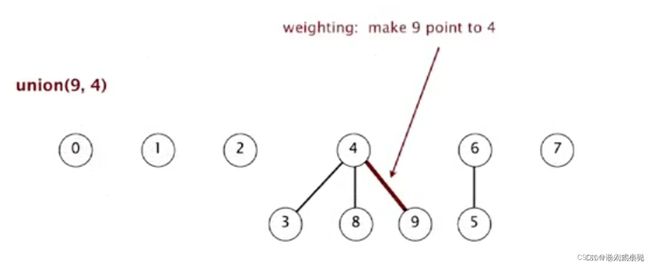
5、union(9,4):4 的根为 8,所以 9 的父亲为 8
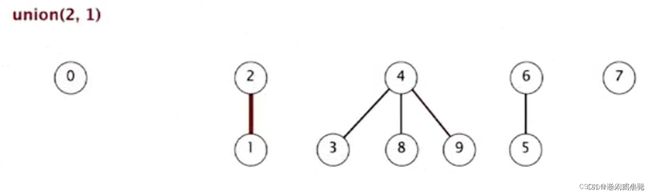
6、union(2,1):2 的父亲为 1
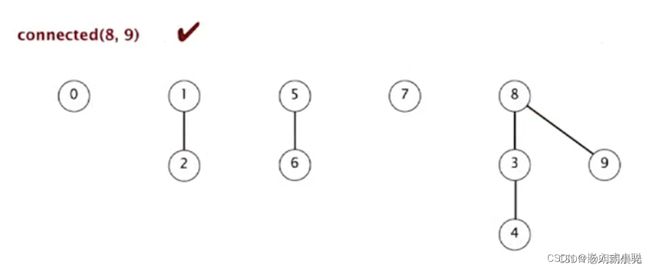
7、connected(8,9):8 和 9 的根相同,所以 8 和 9 是连通的
8、connected(5,4):5 的根为 5, 4 的根为8,二者不同,所以不连通
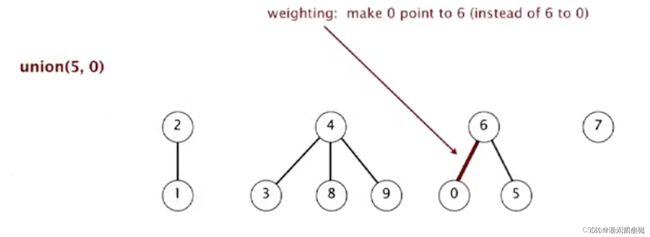
9、union(5,0):5 的父亲是 0
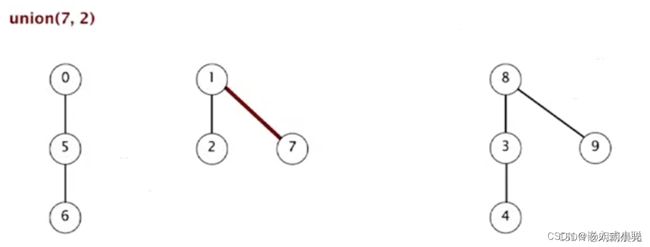
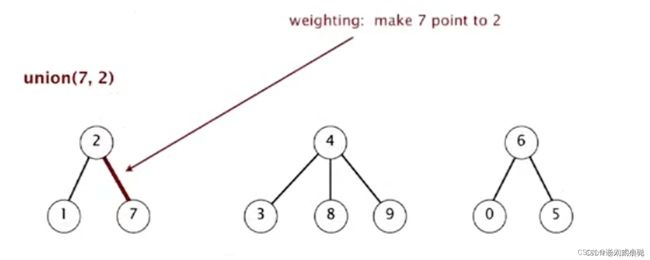
10、union(7,2):2 的根为 1, 所以 7 的父亲是 1
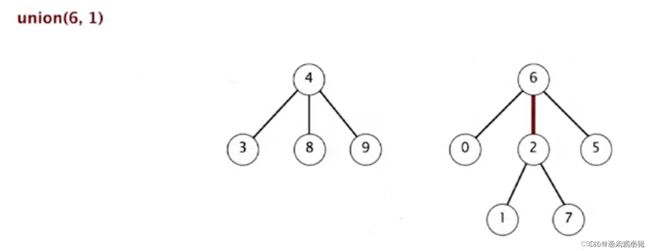
11、union(6,1):6 的根为0, 1 的根为1, 所以 0 是 1 的孩子
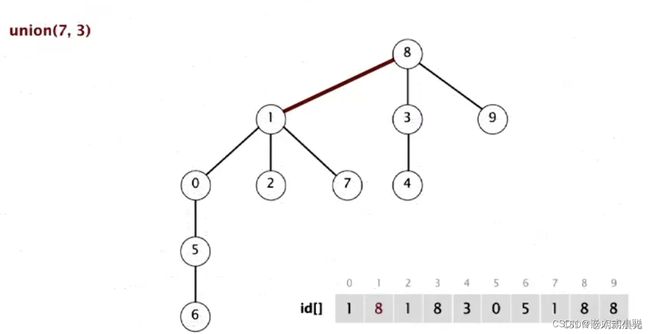
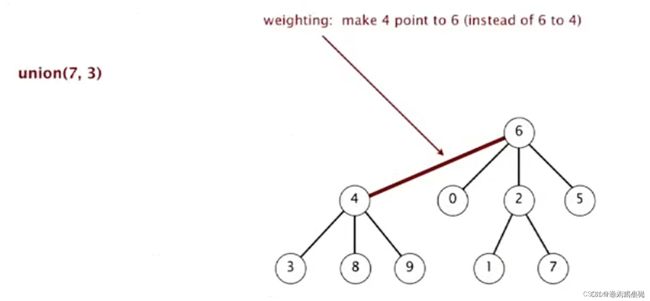
12、union(7,3): 7 的根为1, 3 的根为 8,所以 1 的父亲是 8
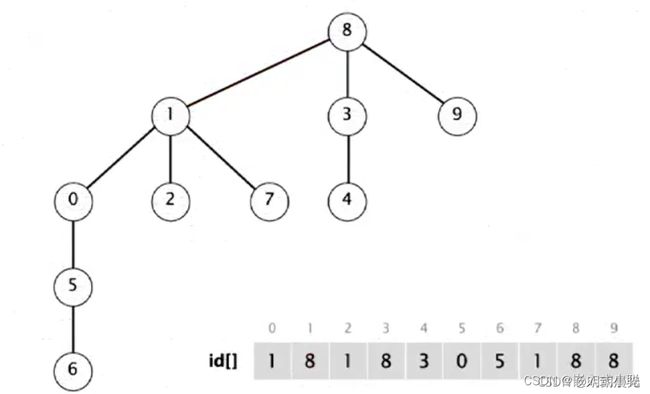
13、最终的结果:
这些 Union 操作中的每一个操作只会更改数组中的一个数据。
代码实现:
#include#include #define MAX_N 10000 int fa[MAX_N + 1]; //记录每个点的根结点 //初始化每个点的值为数组下标 void init(int n) { for (int i = 0; i <= n; i++) fa[i] = i; return ; } //查找某个点的根结点 int find(int x) { if (fa[x] == x) return x; return find(fa[x]); } //合并两棵树(将a变成b的子树) bool merge(int a, int b) { int aa = find(a), bb = find(b); if (aa == bb) return false; fa[aa] = bb; return true; } //打印 void output(int n) { int ret = 0; for (int i = 0; i <= n; i++) ret += printf("%3d", i); printf("\n"); for (int i = 0; i < ret; i++) printf("-"); printf("\n"); for (int i = 0; i <= n; i++) { printf("%3d", fa[i]); } printf("\n"); return ; } int main(int argc, char *argv[]) { int n, a, b; //n:(点的数量) a:(点a) b:(点b) scanf("%d", &n); init(n); //初始化每个点的值为数组下标 while (1) { scanf("%d%d", &a, &b); if ((a >= 0 && a <= n) && (b >= 0 && b <= n)) { if (merge(a, b)) printf("merge %d with %d : %d\n", a, b, merge(a, b)); } else break; output(n); } return 0; }
练习:
四. 按秩合并(Weighted Quick-union)
先找到根,然后将节点少的树合并到节点多的树下,如果发现结点个数相同,就使用
quick-union算法将前面一个节点作为子树合并到后面一个节点子树下
过程演示:
1、起始
2、union(4,3)
3、union(3,8):因为 8 是比较小的树
4、union(6,5):哪个下降都不重要
5、union(9,4):9 是比较小的树,4是比较大的树
6、union(2,1)
7、union(5,0):5所在的树是比较大的树,而0 是小树,所以 0 指向 5 的根 6
8、union(7,2)
9、union(6,1)
10、union(7,3)
11、最终结果:
quick-union中总结中的图对应的weighted quick-union:并查集逻辑思维上可以看作是树结构,
n个集合就是n棵树,而n棵树就是森林。
代码实现:
#include#include #define MAX_N 10000 int fa[MAX_N + 1]; //记录每个点的根结点 int size[MAX_N + 1]; //保存树的结点数量 //初始化每个点的值为数组arr下标和数组size的值为1 void init(int n) { for (int i = 0; i <= n; i++) { fa[i] = i; size[i] = 1; } return ; } //查找某个点的根结点 int find(int x) { if (fa[x] == x) return x; return find(fa[x]); } //合并两棵树(将结点数量较少的树变成结点数量较多的树的子树) bool merge(int a, int b) { int aa = find(a), bb = find(b); if (aa == bb) return false; if (size[aa] < size[bb]) { fa[aa] = bb; size[bb] += size[aa]; } else { fa[bb] = aa; size[aa] += size[bb]; } return true; } //打印 void output(int n) { int ret = 0; for (int i = 0; i <= n; i++) ret += printf("%3d", i); printf("\n"); for (int i = 0; i < ret; i++) printf("-"); printf("\n"); for (int i = 0; i <= n; i++) printf("%3d", fa[i]); printf("\n"); for (int i = 0; i <= n; i++) printf("%3d", size[i]); printf("\n"); return ; } int main(int argc, char *argv[]) { int n, a, b; //n:(点的数量) a:(点a) b:(点b) scanf("%d", &n); init(n); //初始化 while (1) { scanf("%d%d", &a, &b); if ((a >= 0 && a <= n) && (b >= 0 && b <= n)) { if (merge(a, b)) printf("merge %d with %d : %d\n", a, b, merge(a, b)); } else break; output(n); } return 0; }
五. 路径压缩(Weighted Quick-union with path compression)
优化查找过程:扁平化,使得x节点直接指向根
代码实现:
#include#include #define MAX_N 10000 int fa[MAX_N + 1]; int size[MAX_N + 1]; void init(int n) { for (int i = 0; i <= n; i++) { fa[i] = i; size[i] = 1; } return ; } //优化:查找 //return fa[a] = a; //先将a的值赋值给fa[a],然后再返回fa[a]的值(即a)。 int find(int x) //扁平化,使得x节点直接指向根 { return fa[x] = (fa[x] == x ? x : find(fa[x])); } //合并两棵树(将结点数量较少的树变成结点数量较多的树的子树) int merge(int a, int b) { int aa = find(a), bb = find(b); if (aa == bb) return false; if (size[aa] < size[bb]) { fa[aa] = bb; size[bb] += size[aa]; } else { fa[bb] = aa; size[aa] += size[bb]; } return true; } //打印 void output(int n) { int ret = 0; for (int i = 0; i <= n; i++) ret += printf("%3d", i); printf("\n"); for (int i = 0; i < ret; i++) printf("-"); printf("\n"); for (int i = 0; i <= n; i++) printf("%3d", fa[i]); printf("\n"); for (int i = 0; i <= n; i++) printf("%3d", size[i]); printf("\n"); return ; } int main(int argc, char *argv[]) { int n, a, b; //n:(点的数量) a:(点a) b:(点b) scanf("%d", &n); init(n); //初始化 while (1) { scanf("%d%d", &a, &b); if ((a >= 0 && a <= n) && (b >= 0 && b <= n)) { if (merge(a, b)) printf("merge %d with %d : %d\n", a, b, merge(a, b)); } else break; output(n); } return 0; }
六. 练习
1. 海贼OJ #71. 朋友圈
代码实现:
#include#include int colour[10000]; //初始化每个点的颜色为数组下标 void init(int n) { for (int i = 0; i <= n; i++) colour[i] = i; return ; } //查找某个点的颜色 int find(int a) { return colour[a]; } //合并两个集合(全部改成b集合颜色) /* 连通判断:O(1) 合并操作:O(n) */ bool merge(int a, int b, int n) { int aa = find(a), bb = find(b); if (aa == bb) return false; for (int i = 0; i <= n; i++) { if (colour[i] == aa) colour[i] = bb; } return true; } int main(int argc, char *argv[]) { int n, m; int a, b, c; scanf("%d%d", &n, &m); //n:人数 m:操作数 init(n); //初始化颜色 int i = m; while (i--) { scanf("%d%d%d", &a, &b, &c); if (a == 1) merge(b, c, n); if (a == 2) { if (colour[b] == colour[c]) printf("Yes\n"); else printf("No\n"); } } return 0; }
2. 力扣 128. 最长连续序列
代码实现:
1)排序+去重+模拟 超出时间限制
int longestConsecutive(int* nums, int numsSize) { if (numsSize == 0 || numsSize == 1) return numsSize; //冒泡排序 int flag = 1; int i, j; for (i = numsSize - 1; i >= 1 && flag; i--) { flag = 0; for (j = 0; j < i; j++) //j决定哪两个元素进行比较 { if (nums[j] > nums[j + 1]) { flag = 1; int temp = nums[j]; nums[j] = nums[j + 1]; nums[j + 1] = temp; } } } //去重 int *a = malloc(sizeof(int) * numsSize); j = 0; a[j++] = nums[0]; for (i = 1; i < numsSize; i++) { if(nums[i] == nums[i - 1]) continue; else a[j++] = nums[i]; } int max = 1; int len = 1; for (i = 0; i < j - 1; i++) { if (a[i] + 1 == a[i + 1]) { len++; if (len > max) max = len; } else len = 1; } return max; }2)并查集