【数据结构(四)】前缀、中缀、后缀表达式(逆波兰表达式)和逆波兰计算器的代码实现（2）

---

1. 前缀表达式(波兰表达式)

    前缀表达式又称波兰表达式，前缀表达式的运算符位于操作数之前

举例说明： (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6

1.1. 前缀表达式的计算机求值

    从右至左扫描表达式，遇到数字时，将数字压入堆栈；遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素 和 次顶元素），并将结果入栈；重复上述过程直到表达式最左端，最后运算得出的值即为表达式的结果。

例如:
(3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下:
    ①从右至左扫描，将 6、5、4、3 压入堆栈
    ②遇到 + 运算符，因此弹出 3 和 4（3为栈顶元素，4为次顶元素），计算出 3 + 4 的值，得 7，再将 7 入栈
    ③接下来是 × 运算符，因此弹出 7 和 5 ，计算出 7 × 5 = 35，将35入栈
    ④最后是 - 运算符，计算出 35 - 6 的值，即 29 ，由此得出最终结果

2. 中缀表达式

    
    中缀表达式就是常见的运算表达式，如(3+4)×5-6

    中缀表达式的求值是我们人最熟悉的，但是对计算机来说却不好操作(前面我们讲的案例就能看的这个问题)，因此，在计算结果时，往往会将中缀表达式转成其它表达式来操作(一般转成后缀表达式)

3. 后缀表达式(逆波兰表达式)

    后缀表达式又称逆波兰表达式，与前缀表达式相似，只是运算符位于操作数之后

举例说明：

正常表达式	后缀表达式
(3+4)×5-6	3 4 + 5 × 6 –
a+b	a b +
a+(b-c)	a b c - +
a+(b-c)*d	a b c - d * +
a+d*(b-c)	a d b c - * +
a=1+3	a 1 3 + =

3.1. 后缀表达式的计算机求值

    
    从左至右扫描表达式，遇到数字时，将数字压入堆栈；遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素 和 栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果。

例如:
(3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下:

    ①从左至右扫描，将3和4压入堆栈；
    ②遇到 + 运算符，因此弹出 4 和 3（4 为栈顶元素，3 为次顶元素），计算出 3 + 4 的值，得 7 ，再将 7 入栈；
    ③将 5 入栈；
    ④接下来是 × 运算符，因此弹出 5 和 7 ，计算出 7 × 5 = 35 ，将 35 入栈；
    ⑤将 6 入栈；
    ⑥最后是-运算符，计算出 35 - 6 的值，即 29 ，由此得出最终结果

---

3.2. 逆波兰计算器的实现

    
完成一个逆波兰计算器，要求完成如下任务:
    输入一个逆波兰表达式(后缀表达式)，使用栈(Stack), 计算其结果
    支持小括号和多位数整数(因为这里主要讲的是数据结构，因此计算器进行简化，只支持对整数的计算)

    
思路分析： 3.2. 小节已给出
    
代码实现：

package stack;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class PolandNotation {
    public static void main(String[] args) {
        // 定义一个逆波兰表达式
        // (3+4)×5-6 --> "3 4 + 5 × 6 -"
        // 为了方便，逆波兰表达式的数字和符号使用 空格 隔开
        String suffixExpression = "3 4 + 5 * 6 -";

        // 思路
        // 1.先将"3 4 + 5 × 6 -"放到ArrayList中
        // 2.将ArrayList传递给一个方法，利用栈，完成计算
        List<String> rpnList = getListString(suffixExpression);
        System.out.println("rpnList=" + rpnList);

        int res = calculate(rpnList);

        System.out.println("计算的结果是=" + res);

    }

    // 将一个逆波兰表达式，依次将数据和运算符放入到ArrayList中
    public static List<String> getListString(String suffixExpression) {
        // 将suffixExpression分割
        String[] split = suffixExpression.split(" ");
        List<String> list = new ArrayList<String>();
        for (String ele : split) {
            list.add(ele);
        }
        return list;
    }

    // 完成对逆波兰表达式的运算
    /**
     * 1.从左至右扫描，将3和4压入堆栈；
     * 2.到 + 运算符，因此弹出 4 和 3（4 为栈顶元素，3 为次顶元素），计算出 3 + 4 的值，得 7 ，再将 7 入栈；
     * 3.将 5 入栈；
     * 4.接下来是 × 运算符，因此弹出 5 和 7 ，计算出 7 × 5 = 35 ，将 35 入栈；
     * 5.将 6 入栈；
     * 6.最后是-运算符，计算出 35 - 6 的值，即 29 ，由此得出最终结果
     */
    public static int calculate(List<String> ls) {
        // 创建一个栈，只需要一个即可
        Stack<String> stack = new Stack<String>();
        // 遍历 ls
        for (String item : ls) {
            // 这里使用正则表达式来取出数
            if (item.matches("\\d+")) {// 匹配的是多位数
                // 入栈
                stack.push(item);
            } else {
                // pop出两个数，并运算
                int num2 = Integer.parseInt(stack.pop());// 先pop出的数
                int num1 = Integer.parseInt(stack.pop());// 后pop出的数
                int res = 0;
                if (item.equals("+")) {
                    res = num1 + num2;
                } else if (item.equals("-")) {
                    res = num1 - num2;
                } else if (item.equals("*")) {
                    res = num1 * num2;
                } else if (item.equals("/")) {
                    res = num1 / num2;
                } else {
                    throw new RuntimeException("运算符有误");
                }
                // 把res入栈
                stack.push("" + res);
            }
        }
        // 最后留在stack中的数据就是运算结果
        return Integer.parseInt(stack.pop());
    }

}

运行结果：

注：也可以计算多位数，读者可自行测试

4. 中缀表达式 转 后缀表达式

    从前面讲的内容可以看出，后缀表达式适合计算机进行运算，但是人却不太容易写出来，尤其是表达式很长的情况下，因此在开发中，我们需要将 中缀表达式 转成 后缀表达式。

4.1. 思路分析

    

具体步骤如下：

    1.初始化两个栈：运算符栈s1和储存中间结果的栈s2；
    2.从左至右扫描中缀表达式；
    3.遇到操作数时，将其压s2；
    4.遇到运算符时，比较其与s1栈顶运算符的优先级：
      （1）如果s1为空，或栈顶运算符为左括号“ ( ”，则直接将此运算符入栈；
      （2）否则，若优先级比栈顶运算符的高，也将运算符压入s1；
      （3）否则，将s1栈顶的运算符弹出并压入到s2中，再次转到 4.(1) 与s1中新的栈顶运算符相比较；

    5.遇到括号时：
      （1）如果是左括号“ ( ”，则直接压入s1
      （2） 如果是右括号“ ) ”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
    6.重复步骤2至5，直到表达式的最右边
    7.将s1中剩余的运算符依次弹出并压入s2
    8.依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

    
    

---

实例分析：
    下面，以中缀表达式：1 + ((2 + 3) * 4) - 5 为例，实现将其转成后缀表达式。

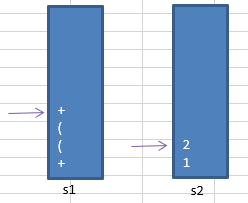
①初始化两个栈：运算符栈s1和储存中间结果的栈s2；从左至右扫描中缀表达式；
②遇到操作数时，将其压s2（首先扫描到 1 ）

③遇到运算符时，比较其与s1栈顶运算符的优先级：
    （1）如果s1为空，或栈顶运算符为左括号“ ( ”，则直接将此运算符入栈（将 + 直接入s1栈，后面连续遇到两个" ( “，根据步骤5.(1)，同理，直接将两个” ( "入s1栈）
    

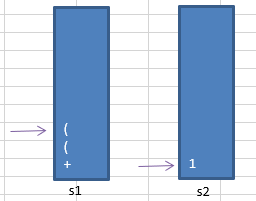
④遇到操作数时，将其压s2（扫描到 2 ）

⑤因为下一个扫描到 + 运算符，而 " ( " 不是运算符，故直接将 + 入s1栈

⑥遇到操作数时，将其压s2（扫描到 3 ）

⑦根据5.(2)：如果是右括号“ ) ”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃

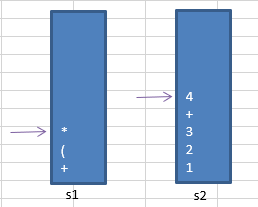
⑧因为下一个扫描到 * 运算符，而 " ( " 不是运算符，故直接将 * 入s1栈；

接着扫描到 4 ，直接入s2栈

⑨根据5.(2)：如果是右括号“ ) ”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃

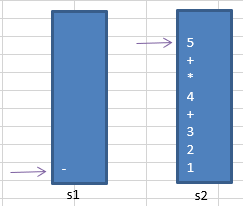
⑩下一个扫描到 - 符号，由于 - 的优先级与 + 相同，故执行 4.(3)：将s1栈顶的运算符弹出并压入到s2中，再次转到 4.(1) 与s1中新的栈顶运算符相比较，由于原来的 + 入了s2栈，即s1栈为空，所以直接将 - 运算符入s1栈。

⑪下一个扫描到 5 ，入s2栈。这时已经到了表达式最右边，扫描完毕

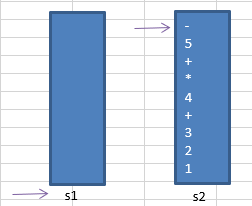
⑫执行步骤7：将s1中剩余的运算符依次弹出并压入s2

⑬步骤8：依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

- 5 + * 4 + 3 2 1 – > 1 2 3 + 4 * + 5 -

通过图表来说明上述步骤：

    

4.2. 代码实现

    

package stack;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class PolandNotation {
    public static void main(String[] args) {

        // 完成将一个中缀表达式转成后缀表达式的功能
        // 说明
        // 1.将 "1+((2+3)*4)-5" 转成 "1 2 3 + 4 * + 5 -"
        // 2.先将 "1+((2+3)*4)-5" -->中缀表达式对应的List
        // 即 "1+((2+3)*4)-5"-->ArrayList[1,+,(,(,2,+,3,),*,4,),-,5]
        String expression = "1+((2+3)*4)-5";
        List<String> infixExpressionList = toInfixExpressionList(expression);
        System.out.println(infixExpressionList);
        System.out.println("中缀表达式对应的List" + infixExpressionList);

        // 3.中缀表达式对应的List --> 后缀表达式对应的List
        // 即将ArrayList[1,+,(,(,2,+,3,),*,4,),-,5] --> ArrayList[1,2,3,+,4,*,5,-]
        List<String> suffixExpressionList = parseSuffixExpressionList(infixExpressionList);
        System.out.println("后缀表达式对应的List" + suffixExpressionList);

        System.out.printf("expression = %d", calculate(suffixExpressionList));

    }

    // 方法：中缀表达式对应的List --> 后缀表达式对应的List
    public static List<String> parseSuffixExpressionList(List<String> ls) {
        // 定义两个栈
        Stack<String> s1 = new Stack<String>();// 符号栈
        // 说明：因为s2这个栈，再整个转换过程中，没有pop操作，而且后面我们还需要逆序输出
        // 此方法比较麻烦，这里就不用Stack,直接使用List s2
        // Stack s2 = new Stack();//存储中间结果的栈s2
        List<String> s2 = new ArrayList<String>();// 存储中间结果的List2

        // 遍历ls
        for (String item : ls) {
            // 如果是一个数，加入s2
            if (item.matches("\\d+")) {
                s2.add(item);
            } else if (item.equals("(")) {
                s1.push(item);
            } else if (item.equals(")")) {
                // 如果是")"，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
                while (!s1.peek().equals("(")) {
                    s2.add(s1.pop());
                }
                s1.pop();// 将"("弹出s1，消除小括号
            } else {
                // 当item的优先级小于s1栈顶运算符，将s1栈顶的运算符弹出并加入到s2中，再次转到(4.1)与s1中新的栈顶运算符相比较
                // 问题：需要一个比较优先级高低的方法
                while (s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)) {
                    s2.add(s1.pop());
                }
                // 将item压入
                s1.push(item);

            }
        }

        // 将s1中剩余的运算符依次弹出并加入s2
        while (s1.size() != 0) {
            s2.add(s1.pop());
        }
        return s2;// 因为是存放到List，因此按顺序输出就是对应的后缀表达式

    }

    // 方法：将中缀表达式转成对应的List
    public static List<String> toInfixExpressionList(String s) {
        // 定义一个List,存放中缀表达式 对应内容
        List<String> ls = new ArrayList<String>();
        int i = 0;// 这是一个指针，用于遍历中缀表达式字符串
        String str;// 对多位数的拼接
        char c;// 每遍历到一个字符，就放入到c
        do {
            // 如果c是一个非数字，需要加入到ls
            if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {
                ls.add("" + c);
                i++;// i需要后移
            } else {// 如果是一个数，需要考虑多位数
                str = "";// 先将str置成"";
                while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {
                    str += c;// 拼接
                    i++;
                }
                ls.add(str);
            }
        } while (i < s.length());
        return ls;
    }

    // 将一个逆波兰表达式，依次将数据和运算符放入到ArrayList中
    public static List<String> getListString(String suffixExpression) {
        // 将suffixExpression分割
        String[] split = suffixExpression.split(" ");
        List<String> list = new ArrayList<String>();
        for (String ele : split) {
            list.add(ele);
        }
        return list;
    }

    // 完成对逆波兰表达式的运算
    /**
     * 1.从左至右扫描，将3和4压入堆栈；
     * 2.到 + 运算符，因此弹出 4 和 3（4 为栈顶元素，3 为次顶元素），计算出 3 + 4 的值，得 7 ，再将 7 入栈；
     * 3.将 5 入栈；
     * 4.接下来是 × 运算符，因此弹出 5 和 7 ，计算出 7 × 5 = 35 ，将 35 入栈；
     * 5.将 6 入栈；
     * 6.最后是-运算符，计算出 35 - 6 的值，即 29 ，由此得出最终结果
     */
    public static int calculate(List<String> ls) {
        // 创建一个栈，只需要一个即可
        Stack<String> stack = new Stack<String>();
        // 遍历 ls
        for (String item : ls) {
            // 这里使用正则表达式来取出数
            if (item.matches("\\d+")) {// 匹配的是多位数
                // 入栈
                stack.push(item);
            } else {
                // pop出两个数，并运算
                int num2 = Integer.parseInt(stack.pop());// 先pop出的数
                int num1 = Integer.parseInt(stack.pop());// 后pop出的数
                int res = 0;
                if (item.equals("+")) {
                    res = num1 + num2;
                } else if (item.equals("-")) {
                    res = num1 - num2;
                } else if (item.equals("*")) {
                    res = num1 * num2;
                } else if (item.equals("/")) {
                    res = num1 / num2;
                } else {
                    throw new RuntimeException("运算符有误");
                }
                // 把res入栈
                stack.push("" + res);
            }
        }
        // 最后留在stack中的数据就是运算结果
        return Integer.parseInt(stack.pop());
    }

}

// 编写一个类Operation，可以返回一个运算符对应的优先级
class Operation {
    private static int ADD = 1;
    private static int SUB = 2;
    private static int MUL = 3;
    private static int DIV = 4;

    // 写一个方法，返回对应的优先级数字
    public static int getValue(String operation) {
        int result = 0;
        switch (operation) {
            case "+":
                result = ADD;
            case "-":
                result = SUB;
            case "*":
                result = MUL;
            case "/":
                result = DIV;
                break;
            default:
                System.out.println("不存在该运算符");
                break;
        }
        return result;
    }
}

运行结果：

5. 逆波兰计算器的完整版

完整版的逆波兰计算器，功能包括：
    ①支持 + - * / ( )
    ②多位数，支持小数,
    ③兼容处理, 过滤任何空白字符，包括空格、制表符、换页符

逆波兰计算器完整版考虑的因素较多，但基本思路和前面一样，也是使用到：中缀表达式转后缀表达式。

代码实现：

package stack;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Stack;
import java.util.regex.Pattern;

public class ReversePolishMultiCalc {

    /**
     * 匹配 + - * / ( ) 运算符
     */
    static final String SYMBOL = "\\+|-|\\*|/|\\(|\\)";

    static final String LEFT = "(";
    static final String RIGHT = ")";
    static final String ADD = "+";
    static final String MINUS = "-";
    static final String TIMES = "*";
    static final String DIVISION = "/";

    /**
     * 加減 + -
     */
    static final int LEVEL_01 = 1;
    /**
     * 乘除 * /
     */
    static final int LEVEL_02 = 2;

    /**
     * 括号
     */
    static final int LEVEL_HIGH = Integer.MAX_VALUE;

    static Stack<String> stack = new Stack<>();
    static List<String> data = Collections.synchronizedList(new ArrayList<String>());

    /**
     * 去除所有空白符
     * 
     * @param s
     * @return
     */
    public static String replaceAllBlank(String s) {
        // \\s+ 匹配任何空白字符，包括空格、制表符、换页符等等, 等价于[ \f\n\r\t\v]
        return s.replaceAll("\\s+", "");
    }

    /**
     * 判断是不是数字 int double long float
     * 
     * @param s
     * @return
     */
    public static boolean isNumber(String s) {
        Pattern pattern = Pattern.compile("^[-\\+]?[.\\d]*$");
        return pattern.matcher(s).matches();
    }

    /**
     * 判断是不是运算符
     * 
     * @param s
     * @return
     */
    public static boolean isSymbol(String s) {
        return s.matches(SYMBOL);
    }

    /**
     * 匹配运算等级
     * 
     * @param s
     * @return
     */
    public static int calcLevel(String s) {
        if ("+".equals(s) || "-".equals(s)) {
            return LEVEL_01;
        } else if ("*".equals(s) || "/".equals(s)) {
            return LEVEL_02;
        }
        return LEVEL_HIGH;
    }

    /**
     * 匹配
     * 
     * @param s
     * @throws Exception
     */
    public static List<String> doMatch(String s) throws Exception {
        if (s == null || "".equals(s.trim()))
            throw new RuntimeException("data is empty");
        if (!isNumber(s.charAt(0) + ""))
            throw new RuntimeException("data illeagle,start not with a number");

        s = replaceAllBlank(s);

        String each;
        int start = 0;

        for (int i = 0; i < s.length(); i++) {
            if (isSymbol(s.charAt(i) + "")) {
                each = s.charAt(i) + "";
                // 栈为空，(操作符，或者 操作符优先级大于栈顶优先级 && 操作符优先级不是( )的优先级 及是 ) 不能直接入栈
                if (stack.isEmpty() || LEFT.equals(each)
                        || ((calcLevel(each) > calcLevel(stack.peek())) && calcLevel(each) < LEVEL_HIGH)) {
                    stack.push(each);
                } else if (!stack.isEmpty() && calcLevel(each) <= calcLevel(stack.peek())) {
                    // 栈非空，操作符优先级小于等于栈顶优先级时出栈入列，直到栈为空，或者遇到了(，最后操作符入栈
                    while (!stack.isEmpty() && calcLevel(each) <= calcLevel(stack.peek())) {
                        if (calcLevel(stack.peek()) == LEVEL_HIGH) {
                            break;
                        }
                        data.add(stack.pop());
                    }
                    stack.push(each);
                } else if (RIGHT.equals(each)) {
                    // ) 操作符，依次出栈入列直到空栈或者遇到了第一个)操作符，此时)出栈
                    while (!stack.isEmpty() && LEVEL_HIGH >= calcLevel(stack.peek())) {
                        if (LEVEL_HIGH == calcLevel(stack.peek())) {
                            stack.pop();
                            break;
                        }
                        data.add(stack.pop());
                    }
                }
                start = i; // 前一个运算符的位置
            } else if (i == s.length() - 1 || isSymbol(s.charAt(i + 1) + "")) {
                each = start == 0 ? s.substring(start, i + 1) : s.substring(start + 1, i + 1);
                if (isNumber(each)) {
                    data.add(each);
                    continue;
                }
                throw new RuntimeException("data not match number");
            }
        }
        // 如果栈里还有元素，此时元素需要依次出栈入列，可以想象栈里剩下栈顶为/，栈底为+，应该依次出栈入列，可以直接翻转整个stack 添加到队列
        Collections.reverse(stack);
        data.addAll(new ArrayList<>(stack));

        System.out.println(data);
        return data;
    }

    /**
     * 算出结果
     * 
     * @param list
     * @return
     */
    public static Double doCalc(List<String> list) {
        Double d = 0d;
        if (list == null || list.isEmpty()) {
            return null;
        }
        if (list.size() == 1) {
            System.out.println(list);
            d = Double.valueOf(list.get(0));
            return d;
        }
        ArrayList<String> list1 = new ArrayList<>();
        for (int i = 0; i < list.size(); i++) {
            list1.add(list.get(i));
            if (isSymbol(list.get(i))) {
                Double d1 = doTheMath(list.get(i - 2), list.get(i - 1), list.get(i));
                list1.remove(i);
                list1.remove(i - 1);
                list1.set(i - 2, d1 + "");
                list1.addAll(list.subList(i + 1, list.size()));
                break;
            }
        }
        doCalc(list1);
        return d;
    }

    /**
     * 运算
     * 
     * @param s1
     * @param s2
     * @param symbol
     * @return
     */
    public static Double doTheMath(String s1, String s2, String symbol) {
        Double result;
        switch (symbol) {
            case ADD:
                result = Double.valueOf(s1) + Double.valueOf(s2);
                break;
            case MINUS:
                result = Double.valueOf(s1) - Double.valueOf(s2);
                break;
            case TIMES:
                result = Double.valueOf(s1) * Double.valueOf(s2);
                break;
            case DIVISION:
                result = Double.valueOf(s1) / Double.valueOf(s2);
                break;
            default:
                result = null;
        }
        return result;

    }

    public static void main(String[] args) {
        // String math = "9+(3-1)*3+10/2";
        String math = "12.8 + (2 - 3.55)*4+10/5.0";
        try {
            doCalc(doMatch(math));
        } catch (Exception e) {
            e.printStackTrace();
        }
    }

}

运行结果：