力扣第二十二题-括号生成

前言

力扣第二十二题 括号生成 如下所示：

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

• 1 <= n <= 8

一、思路

这题共有两种方式，暴力法和回溯

穷举

穷举法：列举所有的排列情况，然后排除非有效的括号

以 n = 3 为例，总共有 2^2*n，即2^6 中排列结果（每一个位置都有两种可能左括号或右括号，共六个位置）

回溯（合理剪枝）

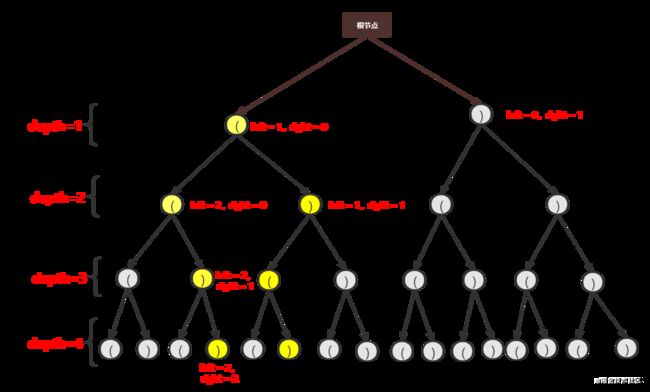
你可以把生成括号的过程想做树的遍历（从根节点向下每个节点都有左右两个子节点，为深度为N的满二叉树）。

那么问题就变成了，如何合理的遍历这个树呢？其实也很简单，既然要组成有效的括号，就排除非有效括号的情况就行了。

要保证生成的是一个有效括号，只需要保证以下两点即可：

1. 如左括号数量需小于N，可添加左括号
2. 如右括号数量小于左括号数量，可添加右括号

以 N=4 做为例子，即有 8 个空位置，从左至右添加括号。只要保证以上两条，最后的括号一定是有效的。
为什么呢？
因为这样可以有效排除右括号先出现，以及左右括号数量不一致的情况

图解回溯（合理剪枝）

此处以 N = 2 为例，会有 4 个可填充的位置
left：已选择左孩子的个数
right：已选择右孩子的个数
黄色：已选择的节点
灰色：已剪枝的节点

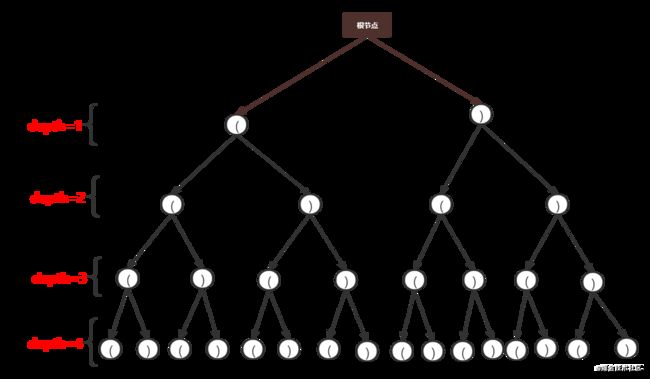
一个N = 2，深度为 4 的完全二叉树如下所示：

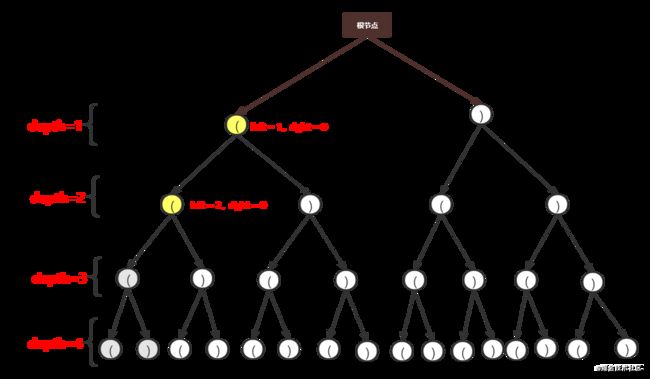
遍历时，先选择左孩子

从根节点开始，先选择左孩子，选择了两次左孩子后如下所示：

继续向下时发现 left = 3, left > 2，此时会剪枝。剪枝后如下所示：

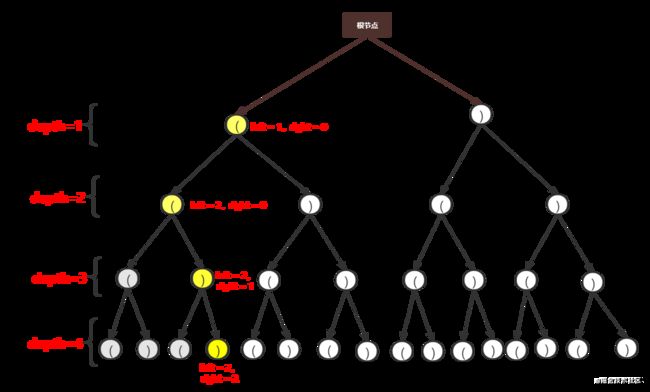
再选择当前节点的右孩子，如下图所示：

继续向下时会发现 left = 3, left > 2，此时会再次剪枝。剪枝后如下所示：

再选择当前节点的右孩子，此时得到了第一个正确的结果 (())，如下图所示：

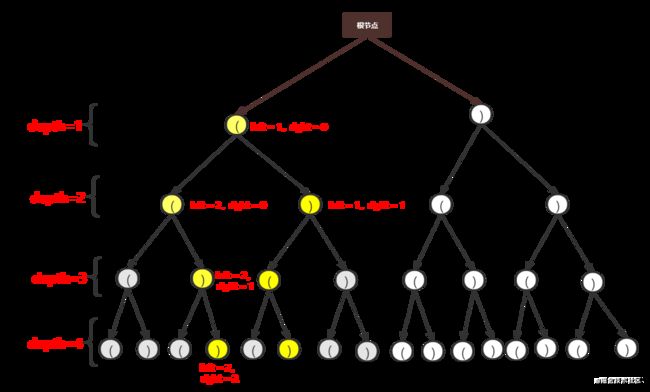
向上回溯，选择 depth = 2的第二个节点。如下所示：

继续向下，可以得到第二个正确的结果 ()()。结果和剪枝如下所示：

继续 向上回溯，会发现 depth=1 的第二个节点需要剪枝。此时 left = 0, right = 1，right > left 需要剪枝。如下图所示：

以上就是在回溯的过程中合理的剪枝了。通过图解的方式，你应该能对回溯有更深的理解了！

二、实现

穷举

实现代码

    public List<String> generateParenthesis(int n) {
        List<String> result = new ArrayList<>();
        generateAll(new char[2 * n], 0, result);
        return result;
    }

    /**
     * 递归生成所有的组合，并去除非有效的括号
     */
    public void generateAll(char[] current, int pos, List<String> result) {
        // 递归结束条件：长度为 2n
        if (pos == current.length) {
            if (valid(current)) {
                result.add(new String(current));
            }
        } else {
            // 当前位置为 (
            current[pos] = '(';
            generateAll(current, pos + 1, result);
            // 当前位置为 )
            current[pos] = ')';
            generateAll(current, pos + 1, result);
        }
    }

    /**
     * 如果在遍历过程中出现右括号多于左括号，则不为有效的括号
     */
    public boolean valid(char[] current) {
        int balance = 0;
        for (char c: current) {
            if (c == '(') {
                ++balance;
            } else {
                --balance;
            }
            if (balance < 0) {
                return false;
            }
        }
        return balance == 0;
    }

测试代码

    public static void main(String[] args) {
        List<String> result = new Number22().generateParenthesis(2);
        for (String str : result) {
            System.out.println(str);
        }
    }

结果

回溯（合理剪枝）

实现代码

tips：无论是添加了左括号还是右括号，都要在之后删除掉，以保证能够正确回溯

    public List<String> generateParenthesis(int n) {
        List<String> result = new ArrayList<>();
        dfs(result, new StringBuilder(), n, 0, 0);
        return result;
    }

    /**
     * 回溯
     * @param ret 结果集
     * @param path 当前遍历的结果
     * @param n 括号的对数
     * @param leftN 左括号数量
     * @param rightN 右括号数量
     */
    public void dfs(List<String> ret, StringBuilder path, int n, int leftN, int rightN) {
        if (path.length() == 2 * n) {
            ret.add(path.toString());
            return;
        }
        // 左括号数量小于n，可添加左括号
        if (leftN < n) {
            dfs(ret, path.append("("), n, leftN + 1, rightN);
            // 删除路径中最后一个元素
            path.deleteCharAt(path.length() - 1);
        }
        // 右括号数量小于左括号数量，可添加右括号
        if (rightN < leftN) {
            dfs(ret, path.append(")"), n, leftN, rightN + 1);
            // 删除路径中最后一个元素
            path.deleteCharAt(path.length() - 1);
        }
    }

结果

三、总结

感谢看到最后，非常荣幸能够帮助到你~♥