数据结构-栈和队列篇

数据结构-栈和队列篇：

---

内容：

1. 思维导图（基于教材）
2. 错题复盘+计算题（基于习题解析）

---

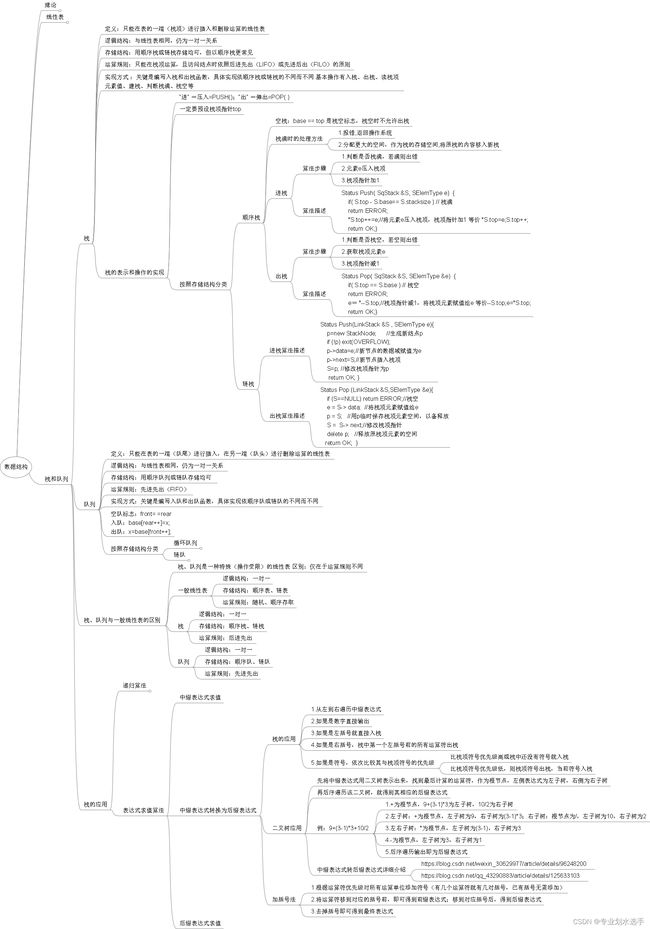
1.思维导图

---

2.错题复盘+计算题

1 若已知一个栈的入栈序列是1，2，3，…n，其输出序列为P1，P2，P3，…，Pn，若P1=n，则Pi为（C）

A.i B.n-i C.n-i+1 D.不确定
解析：一个栈的入栈序列是1，2，3，…n，而其输出P1=n，说明是一次性入栈再一次性输出的，所以P1=n，P2=n-1，Pi=n-i+1

2 设有一个递归算法如下：则计算fact(n)需要调用该函数的次数为（A）

int fact(int n){//n≥0
    if(n<0) return 1;
    else return n*fact(n-1);}

A.n+1 B.n-1 C.n D.n+2
解析：函数递归调用一次，n就减1，从n减到0，才结束递归，所以一共需要n+1次

3 栈在（D）中有所应用

A.递归调用 B.函数调用 C.表达式求值 D.前三个选项都有
解析：编译器是借助栈完成递归调用和函数调用的，在表达式计算中需要通过运算符优先关系来求值，栈都用到了

4 设栈S和队列Q的初始状态为空，元素e1，e2，e3，e4，e5，e6依次进入栈S，一个元素出栈后即进入队列Q，若6个元素出队的序列是e2，e4，e3，e6，e5，e1，则栈S的容量至少为（B）

A.2 B.3 C.4 D.6
解析：由题可知，出栈序列跟出队序列是一样的，再结合入栈序列：e2出栈前，栈里有e2、e1两个元素；e4出栈前，栈里有e4、e3、e1三个元素；e3出栈前，有e3、e1两个元素；e6出栈前，有e6、e5、e1三个；e5出栈前，有e5、e1两个；最后e1出栈。所以至少有3个容量

5 一个递归算法必须包括（B）

A.递归部分
B.终止条件和递归部分
C.迭代部分
D.终止条件和迭代部分

6 若一个栈的入栈序列是1，2，3，…n，输出的第一个元素是i，则第j个输出元素为（D）

A.i-j-1 B.i-j C.j-i+1 D.不确定
解析：栈的出栈序列种数要利用卡特兰公式计算，除非跟第一题一样数据一次性入栈，再一次性出栈才能让数据倒序，这题输出的第一个元素是i，根本不确定第j个能输出啥玩意

7 若用一个大小为6的数组来实现循环队列，且当前rear和front的值分别为0和3，当从队列中删除一个元素，再插入两个元素后，rear和front的值分别为（B）

A.1和5 B.2和4 C.4和2 D.5和1

解析：队头元素出队时，头指针执行Q.front＝（Q.front+1）%M；队尾元素入队时，尾指针rear执行Q.rear=（Q.rear+1）%M。题目说了当前rear和front的值分别为0和3，当从队列中删除一个元素时，front=（3+1）%6=4；再插入两个元素rear=（0+1+1）%6=2

8 设有一个递归算法如下：则计算X(X(8))需要调用该函数的次数为（D）

int X(int n){
    if(n<=3) return 1;
    else return X(n-2)+X(n-4)+1

A.8 B.9 C.16 D.18
解析：如下图所示，先算里面的X(8)，递归9次，算出来的结果是9，然后再化简算最外的递归X(9)，刚好也递归9次，所以一共递归调用了18次

9 四个元素依次进栈，能得到（C）中不同的出栈序列

A.16 B.15 C.14 D.13
解析：4个元素不多，可以用穷举法，一个一个列出来，也可用卡特兰公式f(n)=C(2n,n)/(n+1)计算出栈序列种数，能得到C(24,4)/(4+1)=(8765/4/3/2/1)/5=14种不同的出栈序列

10 设栈的初始状态为空，当字符序列’mp3’作为栈的输入时，输出长度为3，且可以用作C语言标识符的序列有（B）个

A.3 B.4 C.5 D.6
解析：用穷举法更简单，在上题基础上附加个条件就是C语言标识符不能用数字作开头，所以存在mp3、m3p、p3m、pm3这四种输出序列

11 链栈的结点表示为(data,next)，top指向栈顶，则插入一个新结点（用指针x指向）的操作为（B）

A.top->next=x;
B.x->next=top;top=x;
C.x->next=top;top=top->next;
D.x->next=top->next;top->next=x;
解析：链栈在入栈时会先在栈顶插入一个结点，再将栈顶元素指向该结点

12 （B)算法设计策略与递归技术的联系最弱

A.回溯法 B.贪心法 C.分治法 D.动态规划

13 链队中头指针为front，尾指针为rear，则将新结点（用指针x指向）插入队列需要指向的操作是（C）

A.front->next=x;front=front->next;x->next=NULL;
B.rear->next=x;rear=rear->next;
C.x->next=NULL;rear->next=x;rear=rear->next;
D.x->next=rear->next;rear=x
解析：在队列插入新结点时，首先将新结点的指针域x->next置空，表明为尾结点，再将新结点插到链队的尾部，让尾指针rear指向新结点

14 一个空顺序栈的栈顶指针为top=-1，依次执行Push，Push，Pop，Push，Push，Pop，Pop，Push，Push操作后，栈顶指针的值为（B）

A.3 B.2 C.1 D.0
解析：唯一一次遇到这么别出心裁的题目，我连题目都没看懂-_-简单讲模拟出入栈的操作，执行Push操作时，top+1，执行Pop操作时，top-1，加加减减最终top=2

15 最适合用作链队的链表是（B）

A.带头指针和尾指针的循环单链表
B.带头指针和尾指针的非循环单链表
C.只带头指针的非循环单链表
D.只带头指针的循环单链表
解析：队列只允许队尾入队，队头出队。CD的只有头指针，那么入队是从表头开始遍历，再执行入队操作，时间复杂度是O(n)，所以排除；A虽然可以完成队列的操作，但是吧循环单链表要多几步操作，所以是B最合适

16 设循环队列采用一维数组A[0…15]存储，头指针front=10，队列中元素个数size=6，在连续删除两个元素后，队尾位置为（A）

A.0 B.1 C.15 D.17
解析：根据循环队列求解元素个数的公式：元素个数size=(队尾位置rear-队头位置front+M)%M可得rear=0，又因为出队影响的是头指针，所以队尾位置还是0，队头位置为8

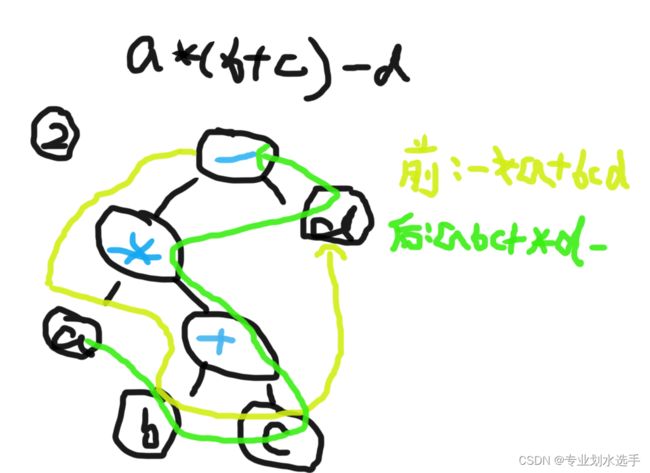
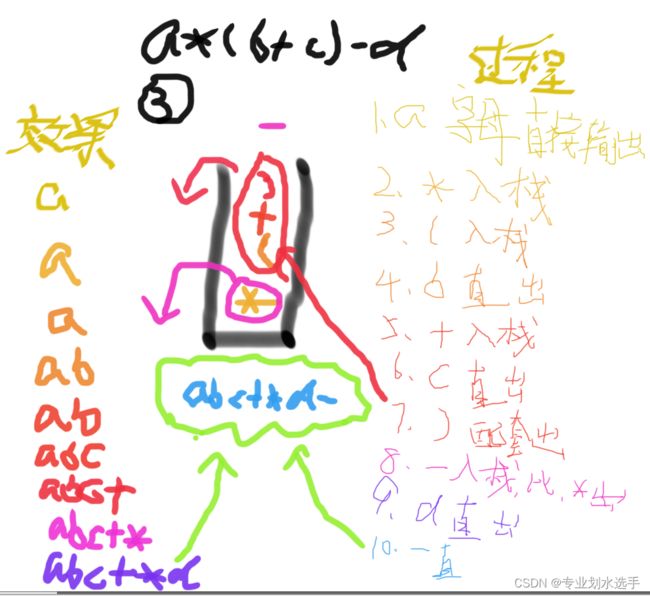
17 表达式a*(b+c)-d的前缀表达式和后缀表达式分别是（B）

A.-+*abcd、abc+*d-
B.-*a+bcd、abc+*d-
C.-a+bcd、abc+d-
D.-+abcd、abc+d-
解析：正如思维导图描述的一样，有3种方式，如下图所示，最好用的就是第一种加括号法了

18 若元素a，b，c，d，e，f依次进栈，允许出栈，退栈操作交替运行，但不允许连续三次进行退栈操作，则不可能得到的出栈序列是（D）

A.d，c，e，b，f，e B.c，b，d，a，e，f C.b，c，a，e，f，d D.a，f，e，d，c，b
解析：穷举法；根据不允许连续三次进行退栈操作要求，可得出栈必定是序列长度<3的连续逆序子序列，D有4个，不符合要求

19 某队列允许在其两端进行入队操作，但仅允许在一端进行出队操作，若元素a，b，c，d，e依次入此队列后再进行出队操作，则不可能得到的出队序列是（C）

A.b，a，c，d，e B.d，b，a，c，e C.d，b，c，a，e D.e，c，b，a，d
解析：穷举法；根据队列的特点，先进先出可得，a、b必定相邻

20 已知循环队列存储在一维数组A[0…n-1]种，且队列非空时front和rear分别指向队头元素和队尾元素。若初始队列为空，且要求第1个进入队列的元素存储在A[0]处，则初始时front和rear的值分别是（B）

A.0、0 B.0、n-1 C.n-1、0 D.n-1、n-1
解析：入队尾指针rear=(rear+1)%n，所以要求第1个进入队列的元素存储在A[0]时，front和rear都指向0，那么rear初值为n-1，front为0

21 求整数n(n≥0)的阶乘的算法如下，其时间复杂度是（B）

long fact(int n){
    if(n<=1) return 1;
    else return (n*fact(n-1));}

A.O(log2n) B.O(n) C.O(nlog2n) D.O(n^2)
解析：设fact(n)的运行时间函数时T(n)。该函数中语句return 1;的运行时间是O(1)，语句return (n*fact(n-1))的运行时间是T(n-1)+O(1)，其中O(1)是常量运行时间

22 操作符包括+-*/()。将中缀表达式a+b-a*((c+d)/e-f)+g转换为等价的后缀表达式ab+acd+e/f-*-g+时，用栈来存放暂时还不能确定运算次序的操作符，若栈初始时为空，则转换过程中同时保存在栈中的操作符的最大个数时（A）

A.5 B.7 C.8 D.11
解析：跟17题的第3种方式一样，这次主要看的是栈里面存放的操作符数量，懒得画了

23 一个栈的入栈序列为1，2，3，…n，其出栈序列为P1，P2，P3…Pn。若P1=3，则P3可能的取值个数时（C）

A.n-3 B.n-2 C.n-1 D.无法确定
解析：除了3本身外，其他值都可以取到

24 假设栈初始为空，在将中缀表达式a/b+(c*d-e*f)/g转换为等价的后缀表达式的过程中，当扫描到f时，栈中的元素依次是（A）

A.+(*- B.+(-* C./+(*-* D./+-*
解析：跟17题的第3种方式一样，这次主要看的是栈里面存放的操作符值，懒得画了

25 已知程序如下：

int S(int n){
    return (n<=0)?0:S(n-1)+n;}
void main(){
    cout<<S(1);}

程序运行时使用栈来保存调用过程的信息，自栈底到栈顶保存的信息依次对应的是（C）
A.main()->S(1)->S(0) B.S(0)->S(1)->main() C.main()->S(0)->S(1) D.S(1)->S(2)->main()
解析：运行程序时，先进入主函数main()，运行语句cout<，调用函数S(1)，然后通过三目运算符判断返回值，最终调用S(0)

26 下列关于栈的叙述中，错误的是（C）

1.采用非递归方式重写递归程序时必须使用栈
2.函数调用时，系统要用栈保存必要的信息
3.只要确定了入栈次序，即可确定出栈次序
4.栈是一种受限的线性表，允许在其两端进行操作
A.仅1 B.仅1、2、3 C.仅1、3、4 D.仅2、3、4
解析：1.采用非递归方式重写递归程序时可以使用栈，但对于单向递归（如Fibonacci数）和尾递归可以用迭代的方式来消除递归。2.正确。3.栈是一种后进先出的线性表，前面几题有做过，知道了入栈序列，不能确定出栈序列。4.栈只允许在其一端进行操作

27 若栈S1中保存整数，栈S2中保存运算符，函数F()依次执行下列各步操作：

1.从S1中依次弹出两个操作数a，b
2.从S2中弹出一个运算符OP
3.执行 b op a
4.将运行结果压入S1
假定S1的操作数依次是5，8，3，2（2在栈顶），S2中的运算符依次是*，-，+（+在栈顶）。调用3次F()后，S1栈保存的值是（B）
A.-15 B.15 C.-20 D.20
解析：F(1) ：3+2=5；S1=5，8，5 F(2)：8-5=3；S1=5，3 F(3)：5*3=15；S1=15

28 现有队列Q与栈S，初始时Q中的元素依次是1，2，3，4，5，6（在队头），S为空。若仅允许下列3种操作：1.出队并输出出队队列 2、出队并将出队元素入栈 3.出栈并输出出栈元素，则不能得到的输出序列是（C）

A.1，2，5，6，4，3 B.2，3，4，5，6，1 C.3，4，5，6，1，2 D.6，5，4，3，2，1
解析：因为队列是先进先出，所以栈的入栈序列=队列序列，而栈先进后出，且输出序列不确定，所以要根据选项反推答案
A.1，2进栈迅速出栈，5出栈的话，说明栈里有4，3，然后6进栈火速出栈，然后4，3出栈
B.2出栈，栈里存1，然后3，4，5，6依次进栈火速出栈，最后把1弹出
C.3出栈，栈里存2，1，然后4，5，6依次进栈火速出栈，然后2，1出栈，所以错误
D.一次性入栈之后，一次性出栈

这章老师倒是没上章讲的细，弄明白栈先进后出，队列先进先出，我期末没考到这章

---