数据结构课程设计(C语言实现)

仅供自己学习使用

---

一、设计任务

  设计一个应用程序（C/C++），利用多级菜单实现单链表、栈、队列、二叉树及图五种结构的基本操作及应用。具体内容包括：

1. 单链表的基本操作及应用
   ①创建
   ②插入
   ③删除
   ④查找
   ⑤应用
   注：利用基本操作（可扩展）实现单链表的应用，如一元多项式运算、通讯录设计等。
2. 栈的基本操作及应用
   ①进栈
   ②出栈
   ③取栈顶元素
   ④应用
   注：利用基本操作（可扩展）实现栈的应用，如表达式求值、深度优先遍历等。
3. 队列的基本操作及应用
   ①入列
   ②出列
   ③取队头元素
   ④取队尾元素
   ⑤应用
   注：利用基本操作（可扩展）实现队列的应用，如酒店客房分配、广度优先遍历等。
4. 二叉树的基本操作及应用
   ①创建
   ②遍历（先序、中序、后序）
   ③求结点个数
   ④求树的深度
   ⑤查找双亲
   ⑥查找兄弟（左/右）
   ⑦查找孩子（左/右）
   ⑧应用
   注：利用基本操作（可扩展）实现二叉树的应用，如二叉排序树、Huffman编码等。
5. 图的基本操作及应用
   ①创建（邻接矩阵/邻接表）
   ②遍历（深度/广度）
   ③定位
   ④找第一个邻接点
   ⑤找下一个邻接点
   ⑥插入（点/边）
   ⑦删除（点/边）
   ⑧应用
   注：利用图的基本操作（可扩展）实现图的应用，如拓扑排序、关键路径等。

二、运行效果图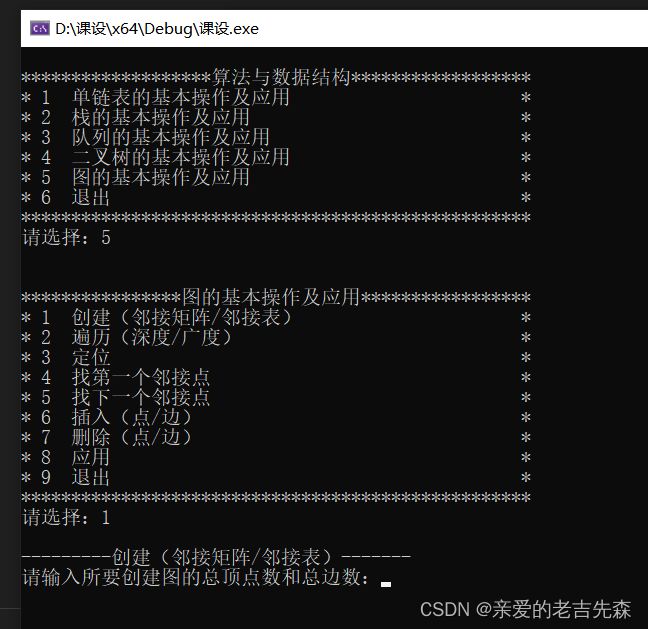

三、部分源代码

1. bitree.h

#include
#include
#include"user.h"

//二叉树结构体
typedef struct BiTNode {
	char data;
	struct BiTNode* lchild, * rchild;
} BiTNode, * BiTree;

//初始化
Status InitBiTree(BiTree& T) {
	T = (BiTree)malloc(sizeof(BiTNode));
	if (!T) {
		printf("内存分配失败。\a\n\n");
	}
	T->lchild = T->rchild = NULL;
	return OK;
}

//先序创建
void CreateBiTree(BiTree& T) {
	char ch;
	printf("请输入结点数据（先序）：");
	scanf_s("%c", &ch);
	getchar();
	if (ch == '*')
		T = NULL;
	else {
		T = new BiTNode;
		T->data = ch;
		CreateBiTree(T->lchild);
		CreateBiTree(T->rchild);
	}
}
//先序遍历
void PreOrderTraverse1(BiTree T) {

	if (T) {
		printf("%c", T->data);
		PreOrderTraverse1(T->lchild);
		PreOrderTraverse1(T->rchild);
	}
}
//中序遍历
void InOrderTraverse2(BiTree T) {

	if (T) {
		InOrderTraverse2(T->lchild);
		printf("%c", T->data);
		InOrderTraverse2(T->rchild);
	}
}
//后序遍历
void PostOrderTraverse3(BiTree T) {

	if (T) {
		PostOrderTraverse3(T->lchild);
		PostOrderTraverse3(T->rchild);
		printf("%c", T->data);
	}
}
//二叉树深度
int Depth(BiTree T) {
	int n, m;
	if (T == NULL)
		return 0;
	else {
		m = Depth(T->lchild);
		n = Depth(T->rchild);
		if (m > n)
			return(m + 1);
		else
			return(n + 1);
	}
}
//叶子结点个数
int LeafCount(BiTree T) {
	if (T == NULL)
	{
		return 0;
	}
	if ((T->lchild == NULL) && (T->rchild == NULL))
	{
		return 1;
	}
	return LeafCount(T->lchild) + LeafCount(T->rchild);
}
//查找双亲
Status Parent(BiTree T, char e)// 初始条件：二叉树T存在，e是T中某个结点
// 操作结果：若e是T的非根结点，则返回它的双亲；否则返回“空”
{
	Status m;
	if (T == NULL) // 空树
		return 0;
	if ((T->lchild && T->lchild->data == e) || (T->rchild && T->rchild->data == e)) {
		printf("结点的双亲数据是：%c\n\n",T->data);
		return OK;
	}
	m = Parent(T->lchild, e);
	if (m == 0)   m = Parent(T->rchild, e);
	return m;
}
//查找兄弟
Status Brother(BiTree T, char e) {
	Status m;
	if (T == NULL) // 空树
		return 0;
	if (T->lchild && T->lchild->data == e) {
		printf("结点存在右兄弟，且右兄弟数据是：%c\n\n", T->rchild->data);
		return OK;
	}
	if (T->rchild && T->rchild->data == e) {
		printf("结点存在左兄弟，且左兄弟数据是：%c\n\n", T->lchild->data);
		return OK;
	}
	m = Brother(T->lchild, e);
	if (m == 0)  m = Brother(T->rchild, e);
	return m;
}

// 查找孩子
Status Child(BiTree T, char e) {
	Status m;
	if (T == NULL) {
		return 0;
	}
	if (T->data == e) {
		if (T->lchild && !T->rchild) {
			printf("存在左孩子，且左孩子数据是：%c\n\n",T->lchild->data);
			return OK;
		}
		if (T->rchild && !T->lchild) {
			printf("存在左孩子，且左孩子数据是：%c\n\n", T->rchild->data);
			return OK;
		}
		if (T->rchild && T->lchild) {
			printf("左孩子数据是：%c，右孩子数据是：%c\n\n",T->lchild->data,T->rchild->data);
			return OK;
		}
	}
	m = Child(T->lchild, e);
	if (m == 0)  m = Child(T->rchild, e);
	return m;
}

// 二叉树的应用


///*********** 测试 *************/
//int main(void) {
//	BiTree root;
//	CreateBiTree(root);
//	printf("\n");
//	//	//printf("先序遍历结果是：");
//	//	//PreOrderTraverse1(root);
//	//	//printf("\n");
//	//	//printf("中序遍历结果是：");
//	//	//InOrderTraverse2(root);
//	//	//printf("\n");
//	//	//printf("后序遍历结果是：");
//	//	//PostOrderTraverse3(root);
//	//	//printf("\n");
//	//	printf("您所创建的二叉树深度是：%d\n\n", Depth(root));
//	//	printf("您所创建的二叉树的叶子结点个数是：%d\n\n", LeafCount(root));
//	//	char data;
//	//	printf("请您输入要查找双亲的结点信息：");
//	//	scanf_s("%c", &data);
//	//	if (!Parent(root, data)) {
//	//		printf("不存在该结点或该结点是根结点。\a\n\n");
//	//	}
//	char data;
//	printf("请您输入要查找兄弟的结点信息：");
//	scanf_s("%c", &data);
//	if (!Child(root, data)) {
//		printf("不存在该结点或该结点是叶子结点。\a\n\n");
//	}
//	return 0;
//}
}

2. LinkList.h

#include
#include
#include"user.h"


typedef struct LNode {
	int data;
	struct LNode* next;
}LNode, *Linklist;

Status ListInit(Linklist& L) { // 初始化
	L = (LNode*)malloc(sizeof(LNode));
	if (!L) {
		printf("内存分配失败！\a\n");
		exit(ERROR);
	}
	L->next = NULL;
	L->data = 0; //头节点的数据存放结点个数
	printf("单链表初始化成功！\n\n");
	return OK;
}

Status ListCreate(Linklist& L) {  // 创建(尾插法)
	int i; // i是循环变量
	int n;//n用于记录元素个数
	printf("请输入元素个数：");
	scanf_s("%d", &n);
	for (i = 0; i < n; i++) {
		LNode* newNode = (LNode*)malloc(sizeof(LNode));
		if (!newNode) {
			printf("内存分配失败！\a\n");
			exit(ERROR);
		}
		printf("\t请输入第%d个元素的数据：", n - i);
		scanf_s("%d", &newNode->data);
		newNode->next = L->next;
		L->next = newNode;
		L->data++;
	}
	printf("单链表创建成功！\n\n");
	return OK;
}

Status ListInsert(Linklist L) {  // 插入
	LNode* sign = L;
	int j = 0;
	int location;
	printf("请输入要插入的位置：");
	scanf_s("%d", &location);
	while (sign && j < location - 1) {
		sign = sign->next;
		++j;
	}
	if (!sign || j > location - 1) {
		printf("位置不合法！\a\n");
		exit(ERROR);
	}
	LNode* newNode = (LNode*)malloc(sizeof(LNode));
	if (!newNode) {
		printf("内存分配失败！\a\n");
		exit(ERROR);
	}
	printf("请输入要插入的数据：");
	scanf_s("%d", &newNode->data);
	newNode->next = sign->next;
	sign->next = newNode;
	L->data++;
	printf("插入成功！\n\n");
	return OK;
}

int ListDelete(Linklist L) {  //删除
	int location;
	printf("请输入要删除元素所在的位置：");
	scanf_s("%d", &location);
	int j = 0;
	LNode* sign = L;
	while (sign->next && j < location - 1) {
		sign = sign->next;
		++j;
	}
	if (!sign || j > location - 1) {
		printf("位置不合法！\a\n");
		exit(ERROR);
	}
	LNode* temp = sign->next;
	sign->next = temp->next;
	int data = temp->data;
	free(temp);
	printf("删除成功！\n\n");
	return data;
}

Status ListShow(Linklist& L) {  //打印
	LNode* sign = L->next;
	int i = 1;
	printf("现在开始打印单链表中的数据：\n");
	while (sign) {
		printf("\t第%d个数据是：%d\n", i++, sign->data);
		sign = sign->next;
	}
	printf("数据打印完毕！\n\n");
	return OK;
}

Status ListLocate(Linklist& L) { //查找
	int data;
	int location = 1; //记录元素位置
	printf("请输入您要查找的元素：");
	scanf_s("%d", &data);
	LNode* sign = L->next;
	while (sign && sign->data != data) {
		sign = sign->next;
		location++;
	}
	if (!sign) {
		printf("当前链表中不存在您要查找的元素。\n\n");
		return FALSE;
	}
	else {
		printf("元素所在位置是第%d个。\n\n", location);
		return OK;
	}
}

// 单链表的应用，多项式相加减
typedef struct pnode
{
	int coef;   //系数
	int exp;   // 指数
	struct pnode* next;  // 后继指针
}PolyNode;

PolyNode* aHead, * bHead;

void DispPoly(PolyNode* head)
{
	PolyNode* p;
	p = head;
	while (p != NULL)
	{
		if (p->coef > 0 && p != head)
		{
			printf("+");
		}
		if (p->exp == 0)
		{
			printf("%d", p->coef);
		}
		else if (p->exp == 1)
		{
			printf("%dx", p->coef);
		}
		else
		{
			printf("%dx^%d", p->coef, p->exp);
		}
		p = p->next;
	}
	printf("\n");
}



void createList(PolyNode*& head)
{
	int m; // m代表多项式的系数
	while (1)
	{
		printf("\n\t\t请输入多项式的项数：");
		scanf_s("%d", &m);
		if (m != 0)
		{
			break;
		}
		else
		{
			printf("\n\t\t不允许输入 0 项！请重新输入！\n");
		}
	}

	PolyNode* p = NULL, * s = NULL;
	for (int i = 0; i < m; i++)
	{

		p = (PolyNode*)malloc(sizeof(PolyNode));
		printf("\n\t\t第%2d项  系数：", i + 1);
		scanf_s("%d", &p->coef);
		printf("\t\t\t指数：");
		scanf_s("%d", &p->exp);
		if (head == NULL)
		{
			head = p;
		}
		else
		{
			s->next = p;
		}
		s = p;
	}

	s->next = NULL;
}

void Add(PolyNode*& ahead, PolyNode*& bhead)
{
	PolyNode* p = NULL, * q = NULL, * s = NULL;
	q = aHead;
	while (q != NULL)
	{
		p = q;
		q = q->next;
	}
	p->next = bHead;
	printf("\n\n\t\t连接：");
	DispPoly(aHead);

	q = aHead;
	while (q != NULL)
	{
		p = q;
		s = q;
		p = p->next;
		while (p != NULL)
		{
			if (p->exp == q->exp)
			{
				q->coef = q->coef + p->coef;
				s->next = p->next;
				free(p);
				p = s;
			}
			s = p;
			p = p->next;
		}
		q = q->next;
	}
	printf("\n\t\t相加得多项式：");
	DispPoly(aHead);
}

void Sub(PolyNode*& ahead, PolyNode*& bhead)
{
	PolyNode* p = NULL, * q = NULL, * s = NULL;
	q = aHead;
	while (q != NULL)
	{
		p = q;
		if (q->coef > 0) q->coef = -(q->coef);
		q = q->next;
	}
	p->next = bHead;
	printf("\n\n\t\t连接：");
	DispPoly(aHead);

	q = aHead;
	while (q != NULL)
	{
		p = q;
		s = q;
		p = p->next;
		while (p != NULL)
		{
			if (p->exp == q->exp)
			{
				q->coef = q->coef + p->coef;
				s->next = p->next;
				free(p);
				p = s;
			}
			s = p;  
			p = p->next;
		}
		q = q->next;
	}
	printf("\n\t\t相减得多项式：");
	DispPoly(aHead);
}

/*********** 测试 *************/
//int main(void) {
//	Linklist L = NULL;
//	ListInit(L); //初始化单链表
//	ListCreate(L); //创建单链表
//	// ListShow(L);  //打印单链表
//	//ListInsert(L);  //插入到单链表
//	//printf("此时单链表中一共有%d个元素.\n", L->data);
//	//ListShow(L);  //打印单链表
//	//ListDelete(L);
//	//ListShow(L);  //打印单链表
//	ListLocate(L);
//}

3. map.h

#include 
using namespace std;
#define MAX 100     //最大顶点数
bool visited[MAX];  //标志数组，用于标记顶点是否被访问过

//边的存储结构
typedef struct BNode
{
	int pointPosite;             //该边所指向顶点的位置
	struct BNode* nextB;         //指向下一条边的指针
	int info;            		 //和边相关的信息
}BNode;

//顶点的存储结构
typedef struct DNode
{
	string data;                //存放顶点信息
	BNode* firstB;              //指针指向第一条依附该顶点的边
}DNode, AdjList[MAX];			//AdjList表领接表类型

//邻接表的存储结构
typedef struct
{
	AdjList vertices;           //顶点向量
	int DNum, BNum;             //图的当前顶点数和边数
}TGraph;

//顺序队列的存储表示
typedef struct
{
	string* base;  	//存储空间的基地址
	int front;		//头指针
	int rear;		//尾指针
}SqQueue;

//队列的初始化
void InitQueue(SqQueue& Q)
{//构造一个空队列
	Q.base = new string[MAX];
	if (!Q.base)
	{
		cout << "内存分配失败" << endl;
	}
	Q.front = Q.rear = 0;
}

// 入队
void EnQueue(SqQueue& Q, string e)
{
	if ((Q.rear + 1) % MAX == Q.front)
	{
		cout << "队列已满" << endl;
	}
	Q.base[Q.rear] = e;
	Q.rear = (Q.rear + 1) % MAX;
}

// 出队
string DeQueue(SqQueue& Q, string& e)
{
	if (Q.front == Q.rear)
	{
		cout << "队列为空" << endl;
	}
	e = Q.base[Q.front];
	Q.front = (Q.front + 1) % MAX;
	return e;
}

// 判断队列是否尾空
bool Empty(SqQueue Q)
{
	if (Q.front == Q.rear)
	{
		return true;
	}
	return false;
}

// 找所给顶点在图中的序号
int LocateVex(TGraph G, string v)
{
	for (int i = 0; i < G.DNum; ++i)
	{
		if (v == G.vertices[i].data)
		{
			return i;
		}
	}
	return -1;
}

// 邻接表创建无向图
void CreateUDG(TGraph& G)       //无向图UDG
{
	string v1, v2;
	cout << "请输入所要创建图的总顶点数和总边数：";
	cin >> G.DNum >> G.BNum;         //输入总顶点数和总边数
	for (int i = 0; i < G.DNum; ++i) //输入各点，构造表头结点表
	{
		cout << "请输入第" << i + 1 << "个顶点的值：";
		cin >> G.vertices[i].data;    //输入顶点值
		G.vertices[i].firstB = NULL;//初始化表头结点指针域为空
	}
	for (int k = 0; k < G.BNum; ++k) //输入各边，构造领接表
	{
		BNode* p1, * p2;
		cout << "请输入第" << k + 1 << "条边的信息：";
		cin >> v1 >> v2;                //输入一条边依附的两个顶点
		int m = LocateVex(G, v1); int n = LocateVex(G, v2); //得到v1 v2在G.vertices中的序号
		p1 = new BNode;         //生成一个新的边结点*p1
		p1->pointPosite = n;    //邻接点序号为n
		p1->nextB = G.vertices[m].firstB;   //头插法
		G.vertices[m].firstB = p1;
		p2 = new BNode;
		p2->pointPosite = m;
		p2->nextB = G.vertices[n].firstB;
		G.vertices[n].firstB = p2;
	}
	cout << "无向图创建成功。\n\n";
}

// 打印图的邻接表
void UDGprint(TGraph G)
{
	BNode* p;
	for (int i = 0; i < G.DNum; ++i)
	{
		cout << G.vertices[i].data;
		p = G.vertices[i].firstB;
		while (p)
		{
			cout << ": ";
			cout << p->pointPosite;
			p = p->nextB;
		}
		cout << endl;
	}
}

// 深度优先遍历
void deepTravel(TGraph G, string v)
{
	int b, w;
	BNode* p;
	cout << v << " ";
	b = LocateVex(G, v);
	visited[b] = true;  //访问第b个顶点，标志为true
	p = G.vertices[b].firstB;    //p指向v的边链表的第一个边结点
	while (p != NULL)            //如果p不为空
	{
		w = p->pointPosite;     //w为v的第一个边结点
		if (!visited[w])         //若w未被访问 则继续递归
		{
			string a;
			for (int i = 0; i < G.DNum; ++i)
			{
				if (w == i)
				{
					a = G.vertices[i].data;
				}
			}
			deepTravel(G, a);
		}
		p = p->nextB;       //否则p指向下一个v的边结点
	}
}

// 广度优先遍历
void breadthTravel(TGraph G, string v)
{
	BNode* p;
	int l;
	string e;
	int b = LocateVex(G, v);
	SqQueue Q;
	InitQueue(Q);
	for (int i = 0; i < G.DNum; i++)
		visited[i] = false;
	if (!visited[b])
	{
		visited[b] = true;
		cout << v << " ";
		EnQueue(Q, v);
		while (!Empty(Q))
		{
			string s = DeQueue(Q, e);
			int u = LocateVex(G, s);
			p = G.vertices[u].firstB;
			while (p)
			{
				l = p->pointPosite;
				if (!visited[l])
				{
					visited[l] = true;
					cout << G.vertices[l].data << " ";
					EnQueue(Q, G.vertices[l].data);
				}
				p = p->nextB;
			}
		}
	}
}

// 查找第一个邻接点
int FirstAdjVex(TGraph G, string v)
{
	BNode* p;
	int v1;
	v1 = LocateVex(G, v);//v1为顶点v在图G中的序号
	p = G.vertices[v1].firstB;
	if (p)
	{
		return p->pointPosite;
	}
	else
	{
		return -1;
	}
}

// 查找下一个邻接点
int NextAdjVex(TGraph G, string v, string w)
{
	BNode* p;
	int v1, v2;
	v1 = LocateVex(G, v);//v1为顶点v在图G中的序号
	v2 = LocateVex(G, w);//v2为顶点v在图G中的序号
	p = G.vertices[v1].firstB;
	for (; p->nextB && p->pointPosite != v2; p = p->nextB);
	if (p->nextB && p->pointPosite == v2)
	{
		return p->nextB->pointPosite;
	}
	else
	{
		return -1;
	}
}

// 插入结点
void InsertNode(TGraph& G, string data)
{
	G.DNum++;
	G.vertices[G.DNum - 1].data = data;
	G.vertices[G.DNum - 1].firstB = NULL;
	printf("插入成功。\n\n");
}

// 删除结点
void DeleteNode(TGraph& G, string data)
{
	int c = LocateVex(G, data);
	BNode* p, * q;
	for (int i = 0; i < G.DNum; ++i)
	{
		p = G.vertices[i].firstB;
		q = p;
		if (G.vertices[i].firstB->pointPosite)
			if (c > G.vertices[i].firstB->pointPosite)
			{
				q = p;
				p = p->nextB;
			}
			else if (G.vertices[i].firstB->pointPosite == c)
			{
				G.vertices[i].firstB = p->nextB;
				q = G.vertices[i].firstB;
				p = p->nextB;
				while (p)
				{
					if (c > p->pointPosite)
					{
						q = p;
						p = p->nextB;
					}
					else
					{
						p->pointPosite -= 1;
						q = p;
						p = p->nextB;
					}
				}
				continue;
			}
			else
			{
				G.vertices[i].firstB->pointPosite -= 1;
				q = p;
				p = p->nextB;
			}
		while (p)
		{
			if (c > p->pointPosite)
			{
				p = p->nextB;
			}
			else if (c == p->pointPosite)
			{
				q->nextB = p->nextB;
				p = p->nextB;

				while (p)
				{
					if (c > p->pointPosite)
					{
						p = p->nextB;
					}
					else
					{
						p->pointPosite -= 1;
						p = p->nextB;
					}
				}
				continue;
			}
			else
			{
				p->pointPosite -= 1;
				q = p;
				p = p->nextB;
			}
		}
	}
	for (int j = 0; j < G.DNum; j++)
	{
		if (G.vertices[j].data == data)
		{
			for (; j < G.DNum; j++)
			{
				G.vertices[j] = G.vertices[j + 1];
			}
			G.DNum -= 1;
			break;
		}
	}
}

/**********应用**********/
// 判断图的联通性
bool Judge(TGraph G)
{
	for (int v = 0; v < G.DNum; v++)
	{
		visited[v] = false;
	}
	deepTravel(G, G.vertices[0].data);                      //从任意一点遍历，这里从下标为0的点开始
	for (int v = 0; v < G.DNum; v++)
	{
		if (!visited[v])
		{
			return false;
		}
	}
	return true;
}


/**************测试***************/
//int main()
//{
//	string ch;
//	TGraph G;
//	CreateUDG(G);
//	cout << "建立的邻接表如下： " << endl;
//	UDGprint(G);
//	cout << "请输入遍历开始的结点：";
//	cin >> ch;
//	cout << "深度遍历序列为： ";
//	deepTravel(G, ch);
//	cout << "\n广度遍历序列为： ";
//	breadthTravel(G, ch);
//	return 0;
//}

完整下载链接

数据结构课程设计