代码随想录-刷题第十天

459. 重复的子字符串

题目链接：459. 重复的子字符串

提示：Java中转为字符数组，不使用charAt()，效率会更高。

思路1：暴力解法。起始下标从0开始，第一个for循环寻找子串的结束位置。只需要遍历到中间位置，因为子串结束位置大于中间位置的话，一定不能重复组成字符串。第二个for循环用来判断子串是否符合条件。

时间复杂度O(n^2)

class Solution {
    public boolean repeatedSubstringPattern(String s) {
        char[] ch = s.toCharArray();
        boolean target = false;
        for (int i = 0; i < ch.length / 2; i++) {
            int k = 0;
            for (int j = 0; j < ch.length; j++, k++) {
                if (k > i) {
                    k = 0;
                }
                if (ch[j] != ch[k]) {
                    break;
                }
            }
            if (k == i + 1) {
                target = true;
            }
        }
        return target;
    }
}

思路2：移动匹配。如果字符串内部可以由字串组成，那么用s+s进行拼接，一定能够从内部再找到一个s。借用随想录中的图片理解一下，如果s如下图。

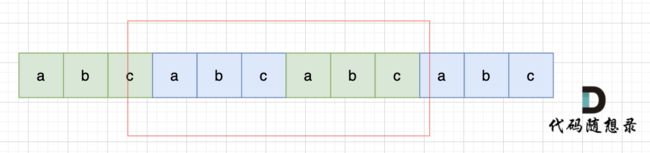
那么s+s就如下图所示。

注意：拼接后的字符串要删除首字符和尾字符，防止在s+s中找出原来的s。

时间复杂度O(m + n)

class Solution { 
    public boolean repeatedSubstringPattern(String s) { 
        // 移动匹配 
        StringBuilder sb = new StringBuilder(); 
        sb.append(s.substring(1)); 
        sb.append(s.substring(0, s.length() - 1)); 
        if (sb.indexOf(s) != -1) { 
            return true; 
        } 
        return false; 
    } 
}

思路3：kmp。重点在于，在由重复子串组成的字符串中，最长相等前后缀不包含的子串就是最小重复子串。具体推导过程移步代码随想录b站讲解。了解这句话后，我们只需要求解next数组，然后判断如果最小重复子串不是整个字符串，并且最小重复子串的长度能够被字符串的长度整除，则说明最小重复子串可以拼接成字符串。

时间复杂度O(n)

class Solution {
    public boolean repeatedSubstringPattern(String s) {
        // kmp
        // 在由重复子串组成的字符串中，最长相等前后缀不包含的子串就是最小重复子串
        char[] ch = s.toCharArray();
        int len = ch.length;
        int[] next = new int[len];
        int j = 0;
        next[0] = 0;
        // 构造 next 数组的过程
        for (int i = 1; i < len; i++) {
            while (j > 0 && ch[i] != ch[j]) {
                j = next[j - 1];
            }
            if (ch[i] == ch[j]) {
                j++;
            }
            next[i] = j;
        }
        // 如果存在最长相等前后缀，
        // 并且最小重复子串的长度能够被字符串长度整除，说明符合条件
        if (next[len - 1] != 0 && len % (len - next[len - 1]) == 0) {
            return true;
        }
        return false;
    }
}

---

字符串总结

双指针法

字符串的题目有的和数组的操作十分相似，可以考虑双指针法。双指针法在数组，链表和字符串中很常用。

反转的题目

这里的很多题目可以考虑，先整体反转再局部反转，或者先局部反转再整体反转。

kmp

kmp主要在匹配子串的题目中用到。重点在于求解next数组。

---

双指针法总结

总结一些双指针法做过的题目。双指针法通常用来降低时间复杂度，提高效率。代码随想录中双指针总结（十分清晰，必看！）

数组类题目

在数组：就移除个元素很难么？中，原地移除数组上的元素，我们说到了数组上的元素，不能真正的删除，只能覆盖。所以此时使用双指针法才展现出效率的优势：通过两个指针在一个for循环下完成两个for循环的工作。

字符串类题目

在字符串：这道题目，使用库函数一行代码搞定中讲解了反转字符串，注意这里强调要原地反转，要不然就失去了题目的意义。

在替换空格中介绍使用双指针填充字符串的方法，如果想把这道题目做到极致，就不要只用额外的辅助空间了！思路就是首先扩充数组到每个空格替换成"%20"之后的大小。然后双指针从后向前替换空格。

那么在字符串：花式反转还不够！中，我们使用双指针法，用O(n)的时间复杂度完成字符串删除类的操作，因为题目要删除冗余空格。在删除冗余空格的过程中，如果不注意代码效率，很容易写成了O(n^2)的时间复杂度。其实使用双指针法O(n)就可以搞定。

链表类题目

在链表：听说过两天反转链表又写不出来了？中，讲如何使用双指针法来翻转链表，只需要改变链表的next指针的指向，直接将链表反转 ，而不用重新定义一个新的链表。

在链表中求环，应该是双指针在链表里最经典的应用，在链表：环找到了，那入口呢？中讲解了如何通过双指针判断是否有环，而且还要找到环的入口。使用快慢指针（双指针法），分别定义 fast 和 slow指针，从头结点出发，fast指针每次移动两个节点，slow指针每次移动一个节点，如果 fast 和 slow指针在途中相遇 ，说明这个链表有环。

n数之和类题目

在哈希表：解决了两数之和，那么能解决三数之和么？中，讲到使用哈希法可以解决1.两数之和的问题。其实使用双指针也可以解决1.两数之和的问题，只不过1.两数之和求的是两个元素的下标，没法用双指针，如果改成求具体两个元素的数值就可以了。使用了哈希法解决了两数之和，但是哈希法并不使用于三数之和！使用双指针法才是最为合适的，用双指针做这道题目才能就能真正体会到，通过前后两个指针不算向中间逼近，在一个for循环下完成两个for循环的工作。

在双指针法：一样的道理，能解决四数之和中，讲到了四数之和，其实思路是一样的，在三数之和的基础上再套一层for循环，依然是使用双指针法。对于三数之和使用双指针法就是将原本暴力O( n^3 )的解法，降为O( n^2 )的解法，四数之和的双指针解法就是将原本暴力O( n^4 )的解法，降为O( n^3 )的解法。同样的道理，五数之和，n数之和都是在这个基础上累加。

---