相关性分析
来源:数学建内容整理
- 选择哪种相关系数?

文章目录
- 一:皮尔逊Person相关系数
-
- 01 数学表达式
- 02 相关性可视化
- 03 皮尔逊相关系数的正确用法
- 04 描述性统计 ※
-
- (1)matlab描述性统计
- (2)Excel描述性统计
- (3)SPSS描述性统计
- 05 皮尔逊相关系数的计算
- 假设检验
-
- 01 检验前的条件
-
- JB检验( 条件:样本量n>30 )
- 夏皮洛-威尔克检验 ( 条件:3≤样本量≤50 )
- Q-Q图 对比 (样本量要非常多)
- 02 开始检验
- 二:斯皮尔曼spearman相关系数
-
- 01 数学表达式
- 02 斯皮尔曼相关系数计算
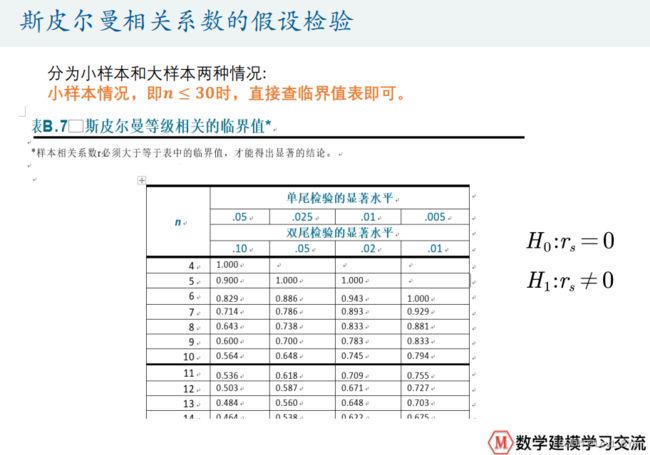
- 03 假设检验
- 自定义matlab

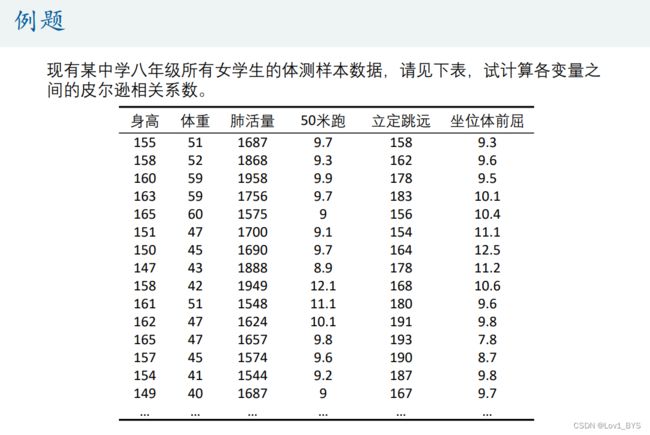
一:皮尔逊Person相关系数
01 数学表达式
02 相关性可视化
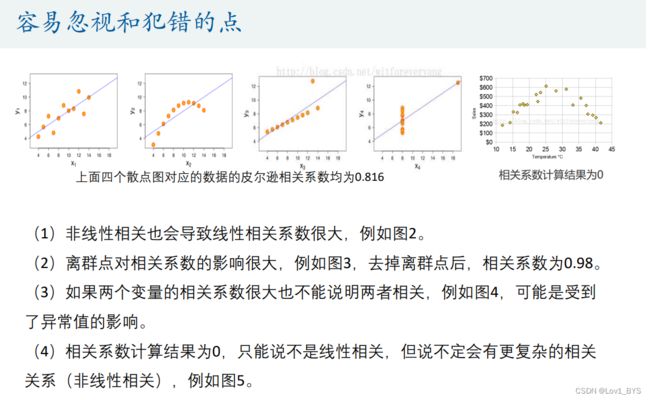
03 皮尔逊相关系数的正确用法
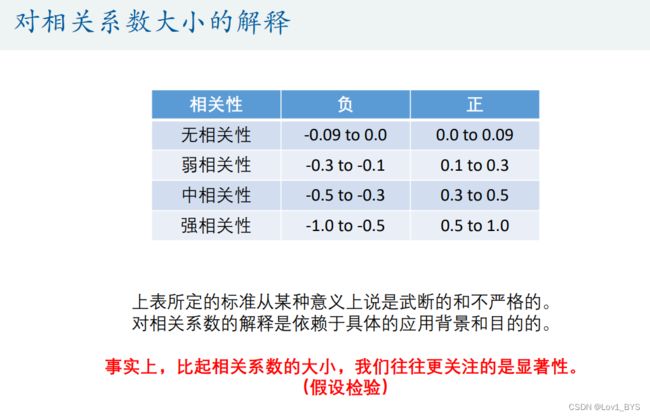
(1)如果两个变量本身就是线性的关系,那么皮尔逊相关系数绝对值大的就是相关性强,小的就是相关性弱;
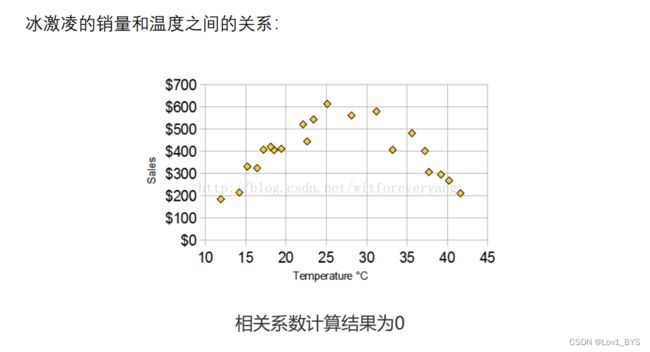
(2)在不确定两个变量是什么关系的情况下,即使算出皮尔逊相关系数,发现很大,也不能说明那两个变量线性相关,甚至不能说他们相关,我们一定要画出散点图来看才行。
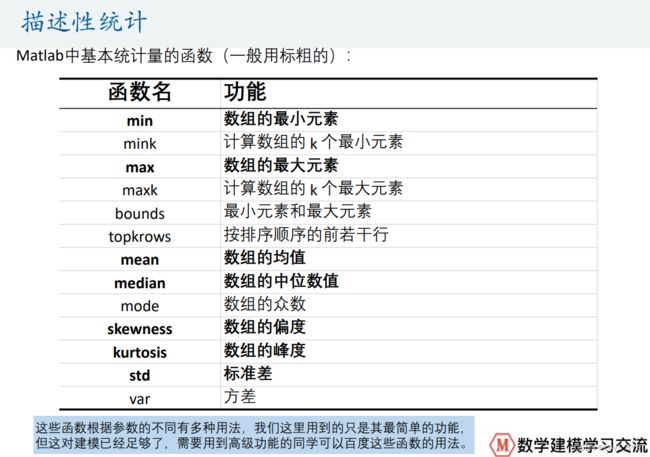
04 描述性统计 ※
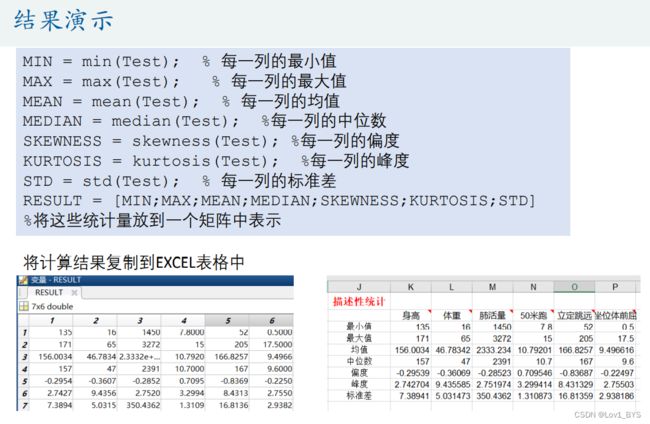
(1)matlab描述性统计
clear;clc load 'physical fitness test.mat' %文件名如果有空格隔开,那么需要加引号 %% 统计描述 MIN =min(Test); % 每一列的最小值 MAX = max(Test); % 每一列的最大值 MEAN = mean(Test); % 每一列的均值 MEDIAN = median(Test); %每一列的中位数 SKEWNESS = skewness(Test);%每一列的偏度 KURTOSIS = kurtosis(Test); %每一列的峰度 STD = std(Test); %每一列的标准差 RESULT = [MIN;MAX;MEAN;MEDIAN;SKEWNESS;KURTOSIS;STD] %将这些统计量放到一个矩阵中表示
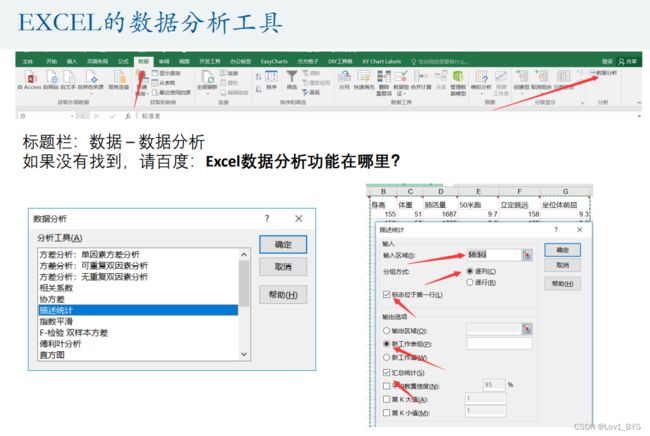
(2)Excel描述性统计
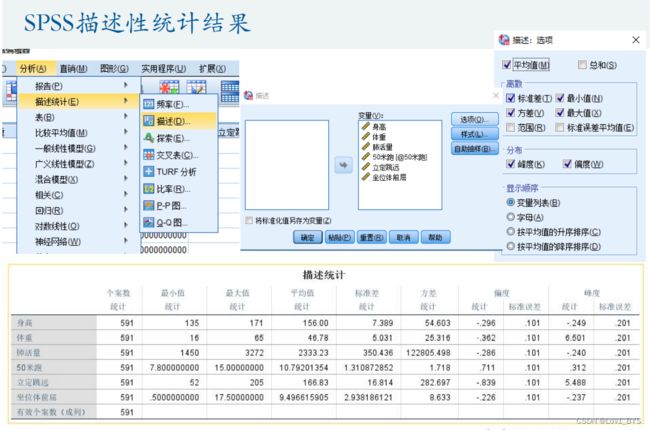
(3)SPSS描述性统计
05 皮尔逊相关系数的计算
%% 计算各列之间的相关系数
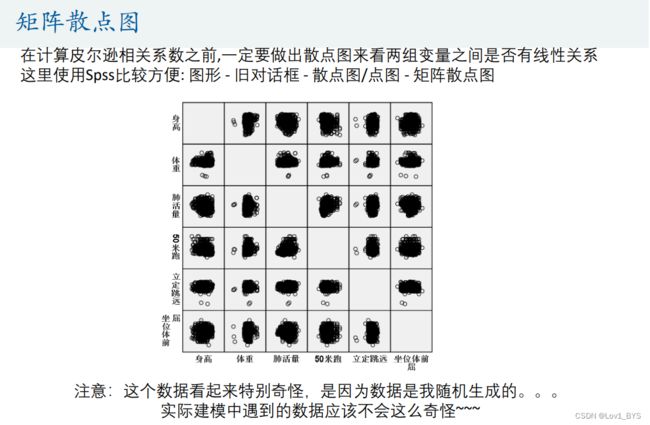
% 在计算皮尔逊相关系数之前,一定要做出散点图来看两组变量之间是否有线性关系
% 这里使用Spss比较方便: 图形 - 旧对话框 - 散点图/点图 - 矩阵散点图
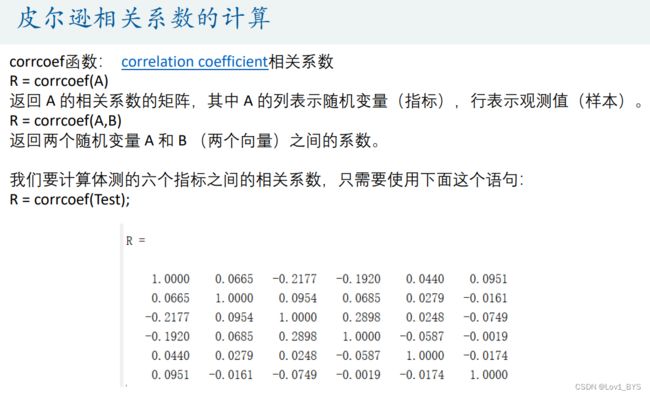
R = corrcoef(Test) % correlation coefficient
-----> 相关系数函数详解
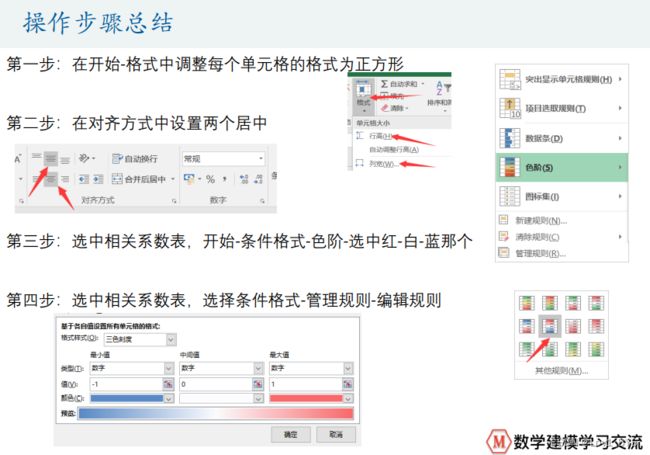
- 美化相关系数表
假设检验
①写出 H 0 H_0 H0 和 H 1 H_1 H1 ;
②在 H 0 H_0 H0 成立条件下,构造一个构造量,该统计量有一个分布;
③在给定置信区间 β β β 下,求出接受域
即 ρ ( a ≤ 统 计 量 ≤ b ) = β ρ(a≤统计量≤b)=β ρ(a≤统计量≤b)=β ( β β β=90%、95%、99%)
④用已知的样本数据代入计算统计量,得到检验值,
若检验落在[a,b]内;则无法拒绝原假设;否则拒绝原假设。
- 先保证满足假设检验条件
- 进行假设检验找出显著性
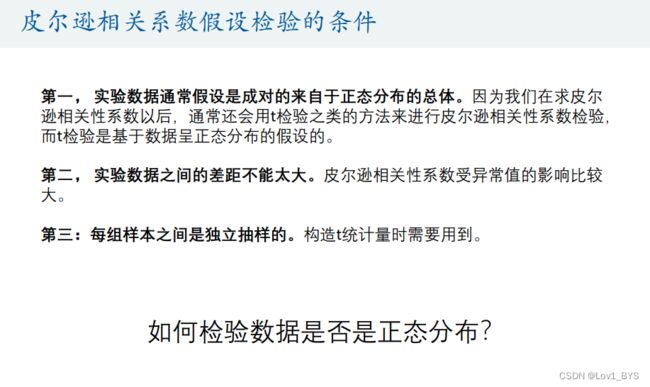
01 检验前的条件
JB检验( 条件:样本量n>30 )
%% 正态分布检验
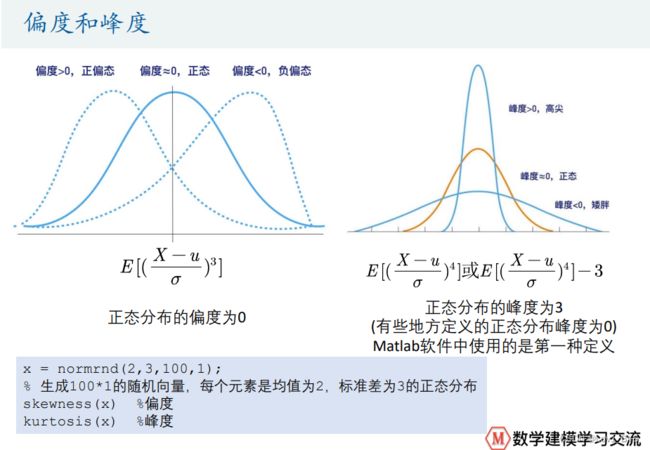
% 正态分布的偏度和峰度
x = normrnd(2,3,100,1); % 生成100*1的随机向量,每个元素是均值为2,标准差为3的正态分布
skewness(x) %偏度
kurtosis(x) %峰度
qqplot(x)
% 检验第一列数据是否为正态分布
[h,p] = jbtest(Test(:,1),0.05)
[h,p] = jbtest(Test(:,1),0.01)
% 用循环检验所有列的数据
n_c = size(Test,2); % number of column 数据的列数
H = zeros(1,6); % 初始化节省时间和消耗
P = zeros(1,6);
for i = 1:n_c
[h,p] = jbtest(Test(:,i),0.05);
H(i)=h;
P(i)=p;
end
disp(H)
disp(P)
%输出等于1时,表示拒绝原假设;h等于0则代表不能拒绝原假设
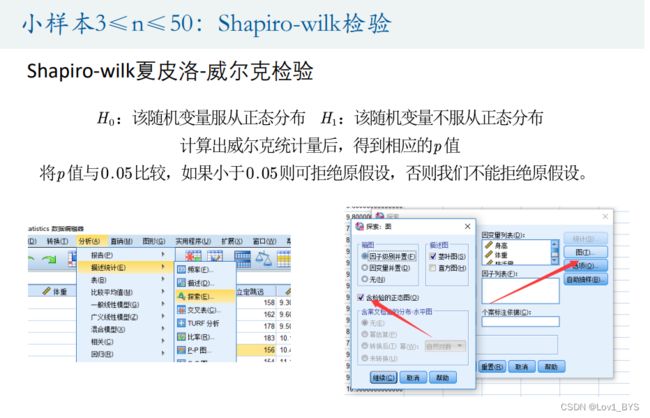
夏皮洛-威尔克检验 ( 条件:3≤样本量≤50 )
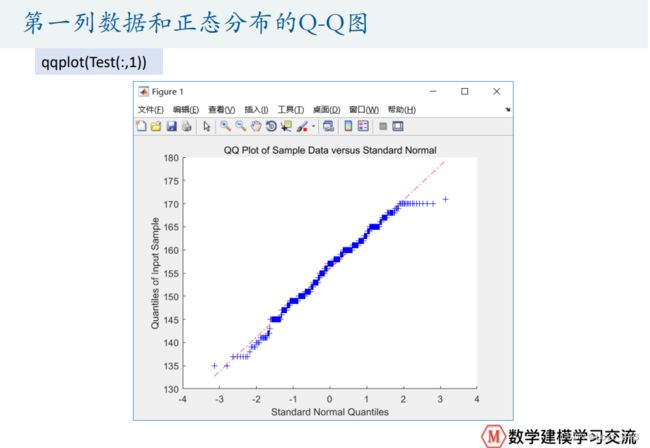
Q-Q图 对比 (样本量要非常多)
% Q-Q图
qqplot(Test(:,1))
02 开始检验
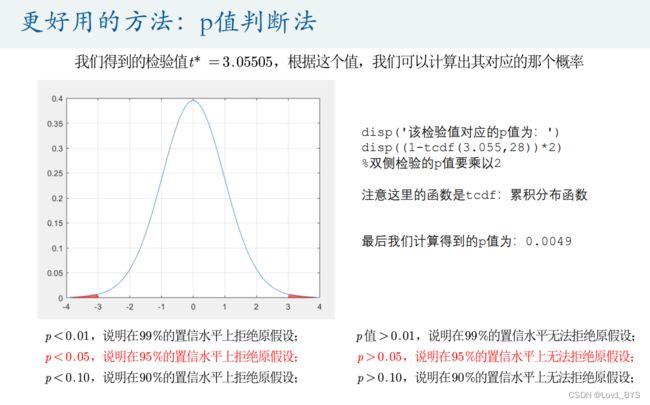
%% 计算p值
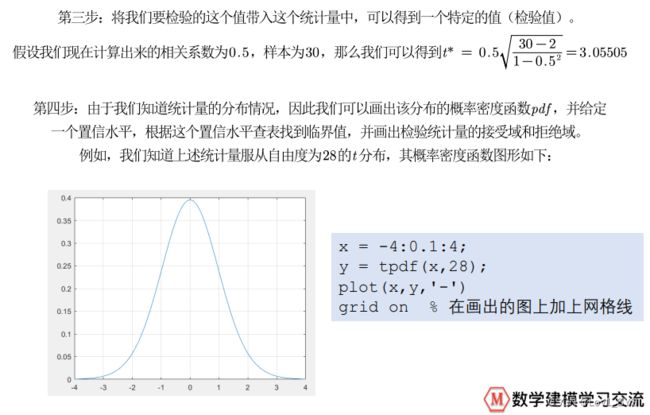
x = -4:0.1:4;
y = tpdf(x,28);
figure(2)
plot(x,y,'-')
grid on
hold on
% 画线段的方法
plot([-3.055,-3.055],[0,tpdf(-3.055,28)],'r-')
plot([3.055,3.055],[0,tpdf(3.055,28)],'r-')
disp('该检验值对应的p值为:')
disp((1-tcdf(3.055,28))*2) %双侧检验的p值要乘以2
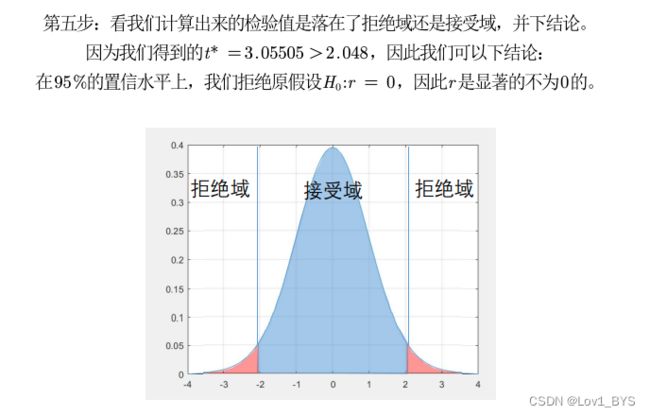
------> t分布查表&https://wenku.baidu.com/view/d94dbd116bd97f192279e94a.html
- 优化
0.5表示不显著; 0.5*表示 p<0.10,说明在90%的置信水平上拒绝原假设; 0.5**表示 p<0.05,说明在95%的置信水平上拒绝原假设; 0.5***表示 p<0.01,说明在99%的置信水平上拒绝原假设;
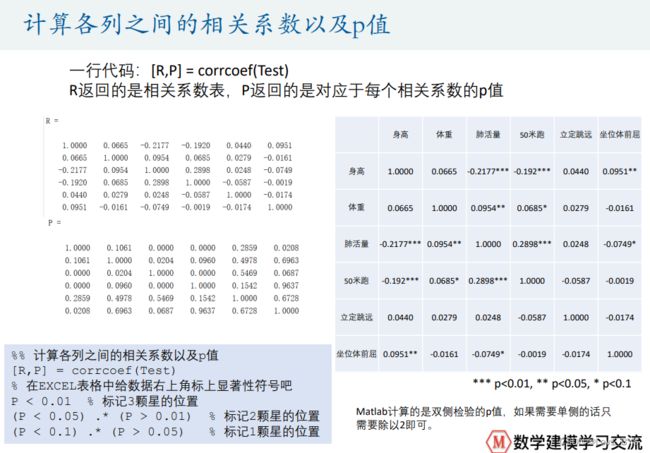
%% 计算各列之间的相关系数以及p值
[R,P] = corrcoef(Test)
% 在EXCEL表格中给数据右上角标上显著性符号吧
P < 0.01 % 标记3颗星的位置
(P < 0.05) .* (P > 0.01) % 标记2颗星的位置
(P < 0.1) .* (P > 0.05) % % 标记1颗星的位置
% matlab只能筛选出,不能标;使用SPSS更方便快捷,可以自动标出*
SPSS操作如下:
分析->相关->双边变量->勾选✔皮尔逊(双尾即双侧检验)->勾选✔标记显著性相关性
二:斯皮尔曼spearman相关系数
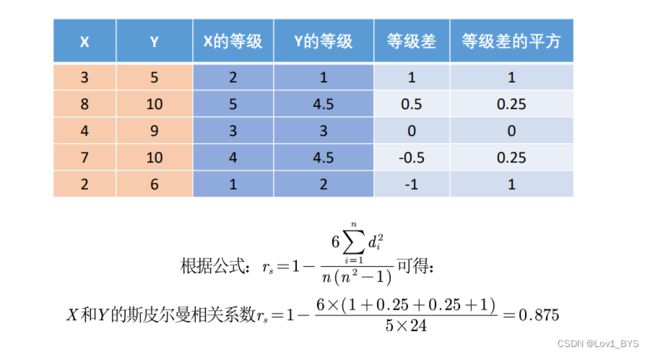
01 数学表达式
X = [3 8 4 7 2]' % 一定要是列向量,一撇'表示求转置
Y = [5 10 9 10 6]'
% 第一种计算方法
1-6*(1+0.25+0.25+1)/5/24
X = [3 8 4 7 2]' % 一定要是列向量,一撇'表示求转置
Y = [5 10 9 10 6]'
% 第二种计算方法
coeff = corr(X , Y , 'type' , 'Spearman')
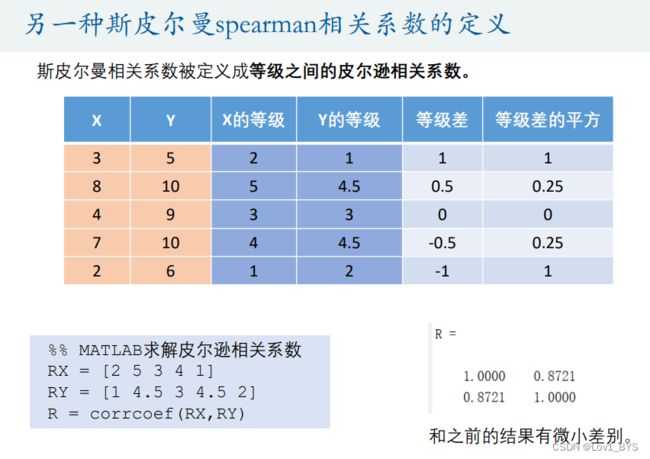
% 等价于:
RX = [2 5 3 4 1]
RY = [1 4.5 3 4.5 2]
R = corrcoef(RX,RY)
02 斯皮尔曼相关系数计算
X = [3 8 4 7 2]' % 一定要是列向量,一撇'表示求转置
Y = [5 10 9 10 6]'
% 计算矩阵各列的斯皮尔曼相关系数
R = corr(Test, 'type' , 'Spearman')
03 假设检验
% 大样本下的假设检验
% 计算检验值
disp(sqrt(590)*0.0301)
% 计算p值
disp((1-normcdf(0.7311))*2) % normcdf用来计算标准正态分布的累积概率密度函数
% 直接给出相关系数和p值
[R,P]=corr(Test, 'type' , 'Spearman')
自定义matlab
- 此代码为第一种方法的计算
(1)加载自定义函数.m文件
- 计算p值的子函数
function [p]= calculate_p(r, m, kind)
% % 输入值:
% r:斯皮尔曼相关系数
% m: 样本个数
% kind: 1表示单侧检验 2表示双侧检验
% % 返回值:
% p:计算出来的p值
z = abs(r) * sqrt(m-1); % 计算检验值 注意这里的相关系数我们先转换为正数再进行计算
p = (1 - normcdf(z)) * kind; % 计算p值,双侧检验的p值是单侧检验的2倍
end
- 计算相关系数r的子函数
function [r]= calculate_r(X, Y)
% % 输入值:
% X: 列向量
% Y: 列向量,且与X同维度
% % 返回值:
% r: X和Y的斯皮尔曼相关系数(第一种定义方法)
RX = rank_data(X); % 调用自定义函数 rank_data 来计算X的等级
RY = rank_data(Y); % 调用自定义函数 rank_data 来计算Y的等级
d = RX - RY; % 计算X和Y等级差
n = size(X,1); % 计算样本个数n
r = 1 - (6 * sum(d .* d)) / (n * (n^2-1)); % 利用公式计算斯皮尔曼相关系数
end
- 排序的子函数
function [RX]= rank_data(X)
% % 输入值:
% X: 列向量
% % 返回值:
% RX: 对应的X的等级
% 举个例子X = [5 10 9 10 6]'
[~ ,index] = sort(X); % ~表示我们不需要第一个输出值(即我们排序后的X [5 6 9 10 10])
% 注意这里的index = [1 5 3 2 4]' 是我们排序后的X在原向量中的位置
[~ ,RX] = sort(index); % 对index进行一次升序,得到的rx就是我们想要的等级 rx = [1 4 3 5 2]'
% 但是这个等级还有一点小问题 ,那就是没有考虑到相等取平均值的问题
for i = 1:size(X,1) % 设置一个循环 (假设此时程序运行到了i = 2)
position = ( X == X(i) ); % 得到X中与X(i)相等的位置,返回一个列向量,向量值全为1或0
% (i= 2时,position = [0 1 0 1 0]' )
RX(position == 1) = sum(RX .* position) / sum(position); % 对RX进行处理
% rx .* position = [0 4 0 5 0]'
% 那么 sum(rx .* position) / sum(position) = (4+5) / 2 = 4.5
% rx(position == 1) = 4.5 : 对rx中与position == 1对应位置的元素(即第2和第4个位置)进行赋值操作
end
end
- 主函数(也为自定义子函数,可以调用)
可计算出X各列之间的相关系数矩阵R和求出对应P值
function [ R , P ]= fun_spearman(X, kind)
% % 输入值:
% X: m*n维数据矩阵,每一行表示一个样本,每一列表示一个指标;且 m >=30 以及 n >= 2
% kind=1: 单侧检验;kind=2: 双侧检验 (不输入默认为2)
% % 返回值:
% R: 斯皮尔曼相关系数矩阵(n*n维)
% P: 对应的p值矩阵(n*n维)
if nargin == 1 % 判断用户输入的参数,如果只输入了一个参数,则默认kind = 2
kind = 2;
end
[m,n] = size(X); % 计算样本个数和指标个数
if m < 30 % 判断是否样本数太少
disp('样本个数少于30,请直接查临界值表进行假设检验')
elseif n <2 % 判断是否指标数太少
disp('指标个数太少,无法计算')
elseif kind ~= 1 && kind ~= 2 % 判断kind是否为1或者2
disp('kind只能取1或者2')
else % 如果上述输入均没问题的话就执行下面的操作
R = ones(n); % 初始化R矩阵
P = ones(n); % 初始化P矩阵
for i = 1: n
for j = (i+1): n % 这样设置循环只计算主对角线上半部分的值
r = calculate_r(X(:, i), X(:, j)); % 用子函数 calculate_r 计算i和j两列的相关系数r
p = calculate_p(r, m, kind); % 用子函数 calculate_p 计算p值
R(i, j) = r; R(j, i) = r; % 把计算出来的相关系数r填充到我们的R矩阵中,注意R矩阵对称
P(i, j) = p; P(j, i) = p; % 把计算出来的p值填充到我们的P矩阵中,注意P矩阵对称
end
end
end
end