李宏毅深度学习课程笔记(一)——Self-attention和Transformer
李宏毅深度学习课程笔记(一)——Self-attention和Transformer
- 1. 前言
- 2. Self-attention
- 3. Multi-head Self-attention
- 4. Position Encoding
- 5. Transformer
-
- 5.1 Encoder
- 5.2 Decoder
- 5.3 Cross Attention
视频课程链接: https://www.bilibili.com/video/BV1Xp4y1b7ih?
1. 前言
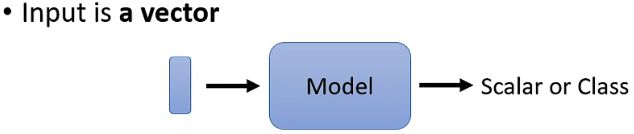
在过去的使用场景中,模型的输入通常只有一个单独的向量,而模型的输出则是预测的数值或类别,如上图。
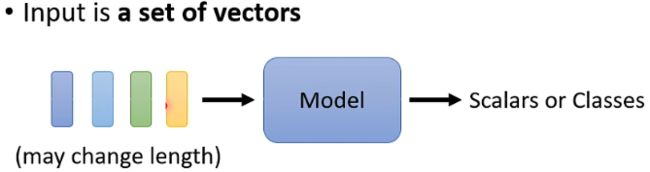
但是假设输入的是一排向量(或序列),且向量的长度不是固定的,例如声音信号、语句、基因序列等,如上图。而对于模型输出而言,可以分为如下图所示的三种类型,即输入输出序列长度不变,只有一个输出和输出长度不确定。

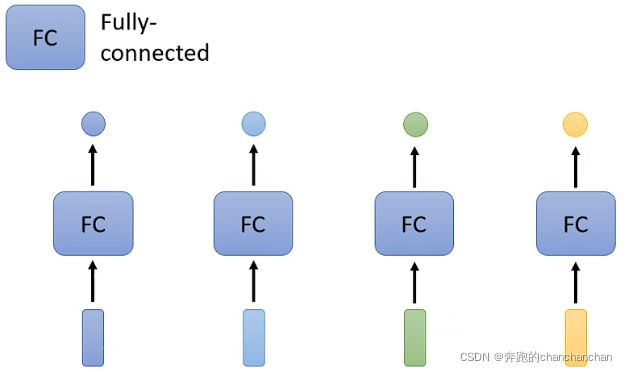
以第一种类型为例,常规的想法是采取各个击破的方法,给每个向量添加一个全连接层,从而得到我们想要的输出,但是这样的方法并没有考虑到各个输入向量之间的关系。
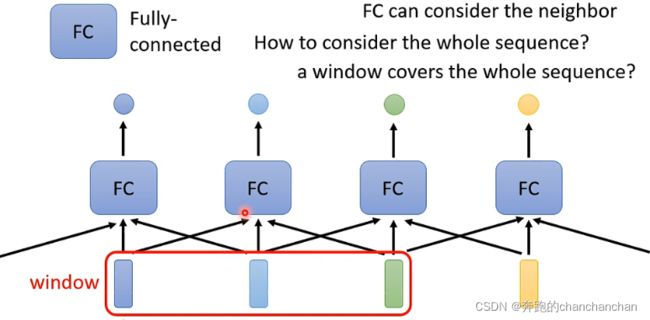
因此为了让全连接层能够考虑到上下文信息之间的关系,可以将多个相邻的输入向量或序列串联起来给到全连接层,但是到底需要多少个相邻的输入向量,以及如何能够把整个序列作为输入,这就是Self-attention所要做的工作。
2. Self-attention

Self-attention的内部机制大致如上图所示,每个输出 b i b^i bi都考虑了所有的输入 a j a^j aj。以单个输出 b 1 b^1 b1为例,Self-attention的具体操作流程如下:
-
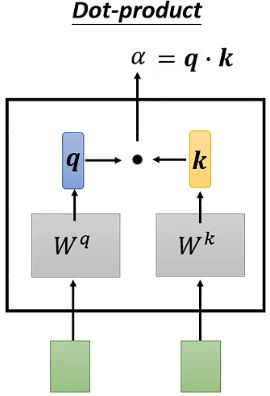
将两个输入向量各自乘以 W q W^q Wq和 W k W^k Wk,得到 q q q和 k k k,再将 q q q和 k k k做点乘,从而得到两个输入向量之间的关联性,记作 α \alpha α。
如下图所示,分别得到输入向量 a 1 a^1 a1和 a 2 a^2 a2之间的关联性 α 1 , 2 \alpha_{1,2} α1,2,输入向量 a 1 a^1 a1和 a 3 a^3 a3之间的关联性 α 1 , 3 \alpha_{1,3} α1,3,输入向量 a 1 a^1 a1和 a 4 a^4 a4之间的关联性 α 1 , 4 \alpha_{1,4} α1,4。
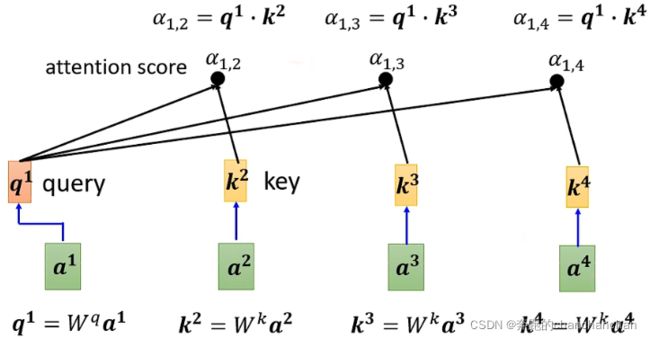
-
通常情况下,还需要计算输入向量与自身的关联性,然后将计算得到的所有关联性 α \alpha α给到Softmax激活函数,得到 α ′ \alpha^{'} α′。

-
根据输入向量之间的关联性 α ′ \alpha^{'} α′进一步提取向量中的重要信息,即将每个输入向量 a i a^i ai乘以 W v W^v Wv得到 v i v^i vi,并与其相关的关联性分数 α 1 , i ′ \alpha^{'}_{1,i} α1,i′相乘,最后将结果累加得到 b 1 b^1 b1。
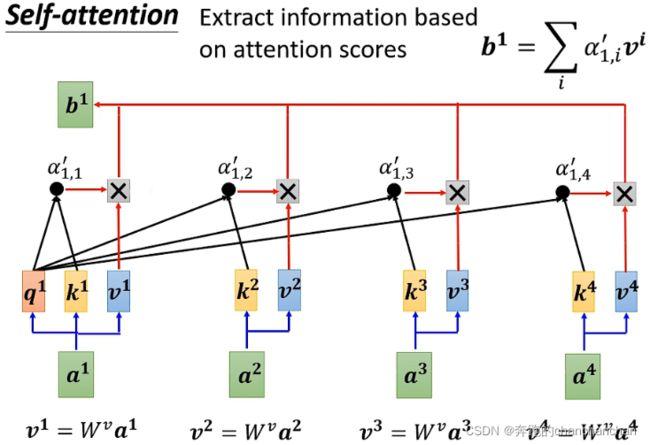 这样一来,假设输入向量 a 1 a^1 a1和 a 2 a^2 a2之间的关联性较大,即 α 1 , 2 ′ \alpha^{'}_{1,2} α1,2′的值较大,根据累加得到的 b 1 b^1 b1也会更加接近 α 1 , 2 ′ \alpha^{'}_{1,2} α1,2′。
这样一来,假设输入向量 a 1 a^1 a1和 a 2 a^2 a2之间的关联性较大,即 α 1 , 2 ′ \alpha^{'}_{1,2} α1,2′的值较大,根据累加得到的 b 1 b^1 b1也会更加接近 α 1 , 2 ′ \alpha^{'}_{1,2} α1,2′。
实际上,Self-attention的输出 b 1 b^1 b1、 b 2 b^2 b2、 b 3 b^3 b3、 b 4 b^4 b4可以同时得到。从矩阵运算的角度来说,Self-attention的具体操作流程如下:
- 将输入向量 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4按列组合成一个矩阵 I I I,与 W q W^q Wq相乘得到矩阵 Q Q Q,其中矩阵 Q Q Q包含了所有输入向量对应的 q u e r y query query,同理可以得到 k e y key key和 v a l u e value value对应的矩阵 K K K和 V V V。
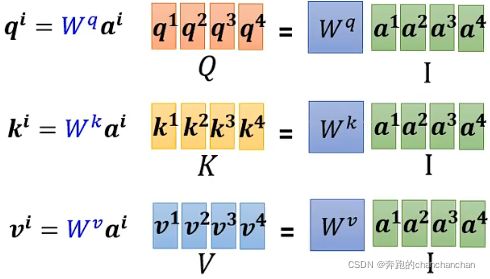
- 将各个向量对应的 k e y key key按行组合,与输入向量 a 1 a^1 a1相乘,得到与输入向量 a 1 a^1 a1之间的所有关联性分数 a 1 , 1 a_{1,1} a1,1、 a 1 , 2 a_{1,2} a1,2、 a 1 , 3 a_{1,3} a1,3、 a 1 , 4 a_{1,4} a1,4。

由此可知,将矩阵 K K K转置后,与矩阵 Q Q Q相乘得到矩阵 A A A,其中矩阵 A A A包含了所有输入向量之间的关联性分数。

然后再将矩阵 A A A给到Softmax激活函数,得到矩阵 A ′ A^{'} A′。
- 最后将各个输入向量对应的 v a l u e value value按列组合成一个矩阵 V V V,并与矩阵 A ′ A^{'} A′相乘得到Self-attention的输出矩阵 O O O。

3. Multi-head Self-attention
因为两者之间的关联性具有不同的定义和形式,因此需要不同的参数矩阵 Q Q Q、 K K K和 V V V来定义不同种类的关联性。Multi-head Self-attention就是由多个单独的Self-attention堆叠而成,每个Self-attention之间具有独立的参数矩阵,相互之间不共享参数。
以2 heads为例,首先通过输入向量 a i a^i ai与矩阵 W q W^q Wq相乘得到 q i q^i qi,再将向量 q i q^i qi与2个不同的矩阵相乘得到两个参数 q i , 1 q^{i,1} qi,1和 q i , 2 q^{i,2} qi,2,同理可以得到参数 k i , 1 k^{i,1} ki,1、 k i , 2 k^{i,2} ki,2、 v i , 1 v^{i,1} vi,1和 v i , 2 v^{i,2} vi,2。对于另一个输入向量 a j a^j aj,同样可以得到两组参数 q j , 1 q^{j,1} qj,1和 q j , 2 q^{j,2} qj,2, k j , 1 k^{j,1} kj,1和 k j , 2 k^{j,2} kj,2, v j , 1 v^{j,1} vj,1和 v j , 2 v^{j,2} vj,2。
在计算关联度分数时,只需先对第一类的参数进行计算,得到 b i , 1 b^{i,1} bi,1,如下图所示。

再对第二类的参数进行计算,得到 b i , 2 b^{i,2} bi,2,如下图所示。
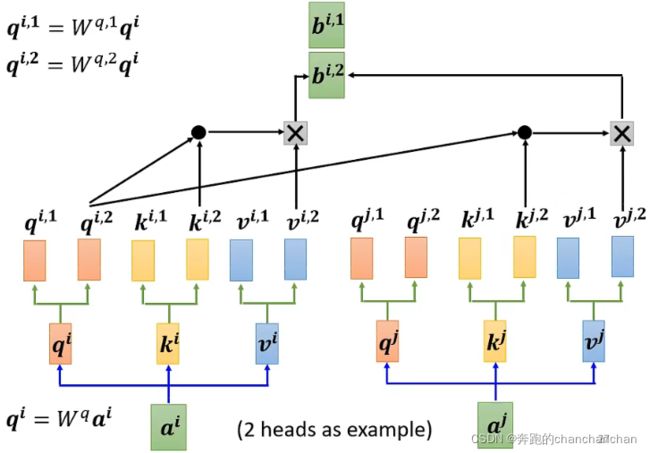
最后将 b i , 1 b^{i,1} bi,1和 b i , 2 b^{i,2} bi,2拼接起来,与矩阵 W O W^O WO相乘得到Multi-head Self-attention的第 i i i个输出 b i b^i bi。

4. Position Encoding
由于在Self-attention的计算中不包含位置信息,因此为了加入位置信息,需要在每个位置都定义一个位置向量 e i e^i ei,并且直接加到输入向量 a i a^i ai上。

位置向量 e i e^i ei通常是手动设置,也可以通过学习得到。
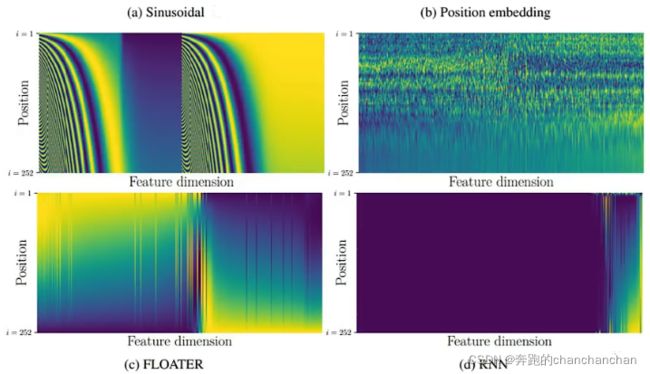
5. Transformer
Transformer本质上是一个Sequence-to-sequence(Seq2seq) 的模型,它的输出序列长度不再是固定的,而是由模型自身决定。
Sequence-to-sequence(Seq2seq) 的模型结构通常如上图所示,由Encoder对输入向量(或序列)进行处理,处理完之后给到Decoder,并由Decoder决定输出向量(或序列)。
5.1 Encoder
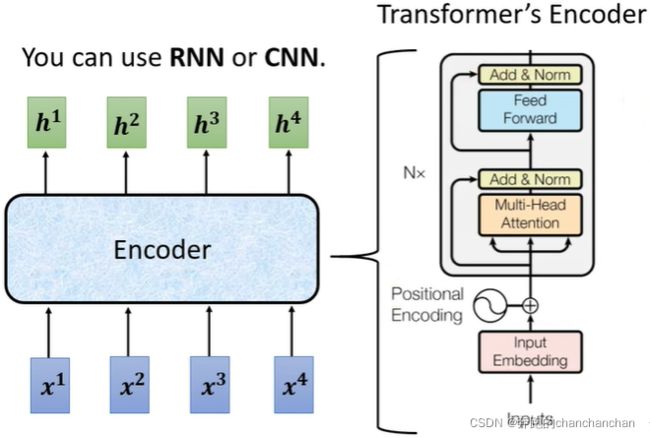
其中Encoder部分的作用是给定一组向量(或序列),输出一组相同长度的向量(或序列),如上图。
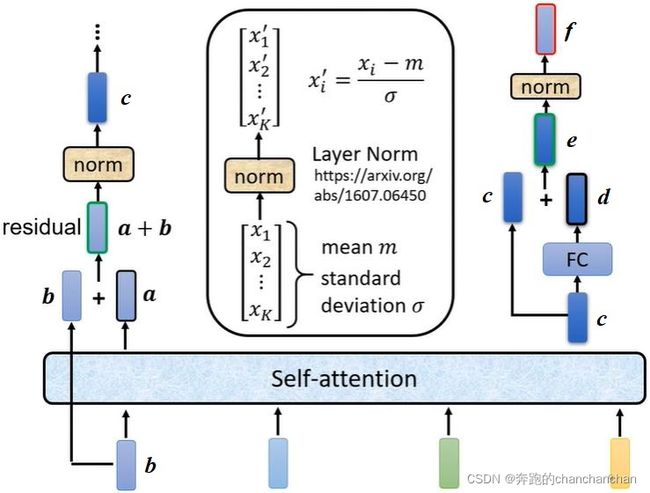
根据原论文Attention Is All You Need中的介绍,进一步拆解它的内部结构可以看到,输入向量 b b b经过Self-attention得到向量 a a a,同时由相应的输入向量 b b b通过跳跃连接与向量 a a a相加,经过一次Layer Norm操作后得到向量 c c c。将向量 c c c给到全连接层得到向量 d d d,并与自身通过跳跃连接相加得到向量 e e e,最后再做一次Layer Norm操作得到向量 f f f。
5.2 Decoder
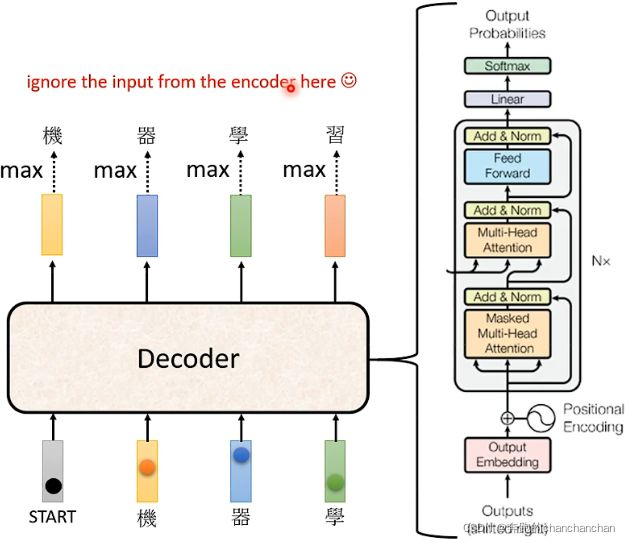
根据原论文Attention Is All You Need中的介绍,Decoder的内部结构如上图所示。
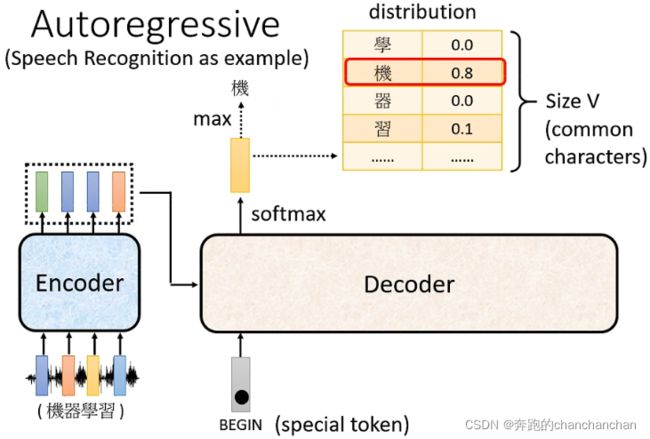
在Decoder中,Encoder的输出在经过cross attention处理之后,来作为Decoder的输入,另外还需要给予一个one-hot形式的BEGIN信号让Decoder开始输出一个向量。在NLP任务中,这个向量的长度由任务所需要的语言单词或短语的数量来决定,例如识别的语言是中文,那么这个向量可能就需要包含所有的中文汉字或常见字。同时为了让模型自己决定需要输出多长的序列,向量中还包含了一个END信号。向量中的每个单词或短语都带有对应的模型预测概率,概率最高的那一项才是最终的输出。
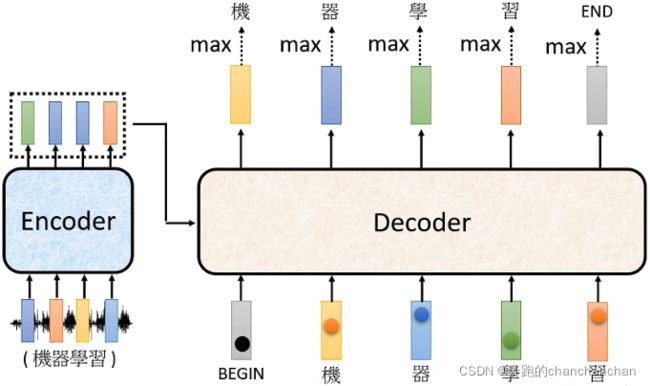
接下来再将第一个输出给到Decoder,作为新的输入,从而得到第二个输出。以此为例,新的输出再次给到Decoder中,直到输出END信号表示向量输出的结束。
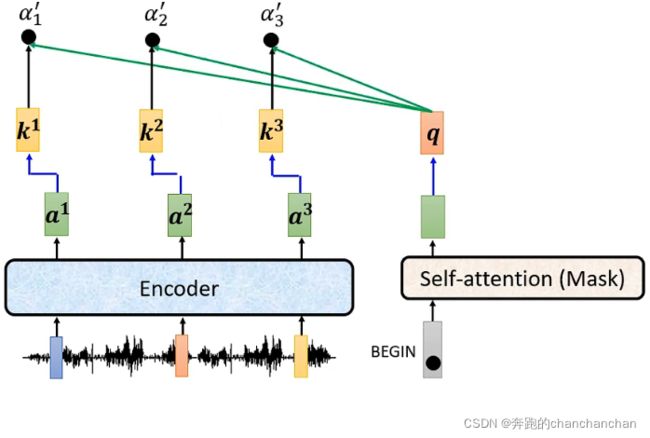
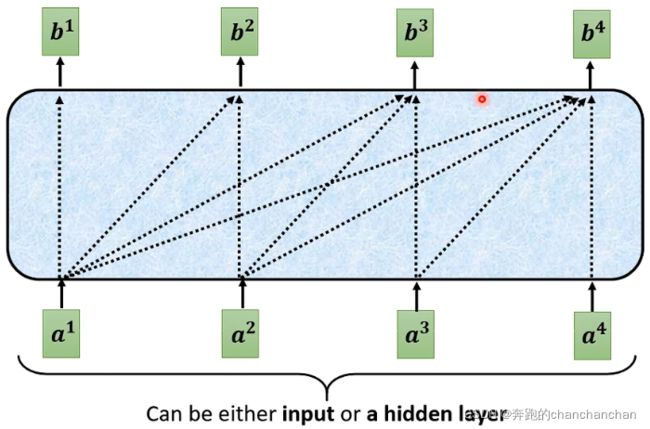
正是因为新的输入是由之前的输出所得到的,因此在Decoder中使用了Masked Multi-Head Attention,与Encoder中的Multi-Head Attention所不同的是,在计算输出的时候只考虑自身及其左边的输入向量,而不需要考虑右边那些还没得到的输入向量,如下图。
5.3 Cross Attention
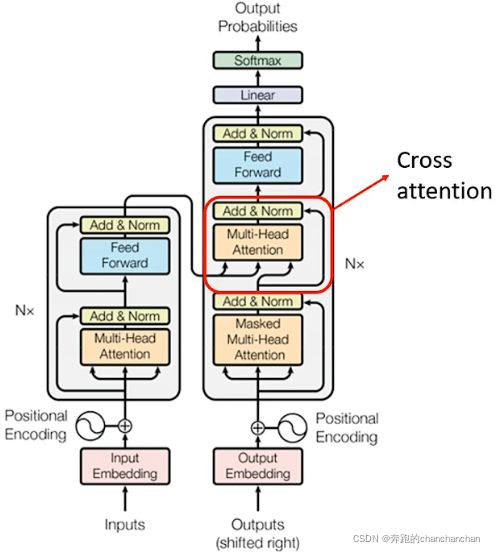
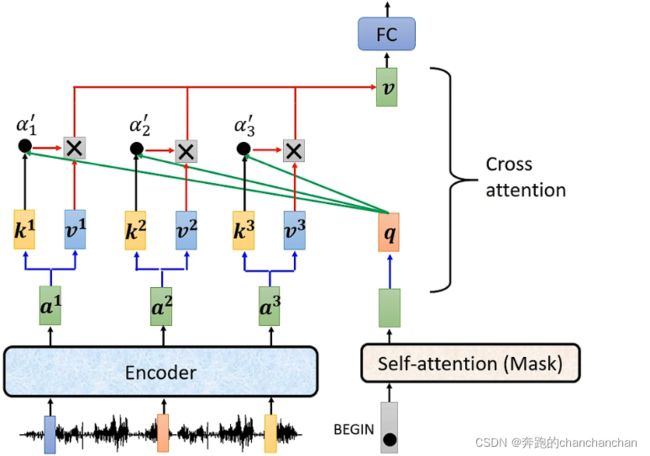
Decoder部分不仅有自身的输入向量,还有Encoder部分的输出作为输入向量。而Encoder部分的输出与Decoder中Masked Multi-Head Attention的输出一起被送到Multi-Head Attetion进行处理,这部分就叫Cross Attention,如上图。
Cross Attention的具体实现流程如下: