【AC.HASH】OpenHarmony啃论文俱乐部——哈希技术：综述和分类(译)

• 本文出自 AC.HASH 团队，AC<=>Adaptive Creator，适应性创作者，旨在于能够在未来新领域下创造出新的哈希算法以应对未来局面。
• 产出本文的成员：
  • 中原工学院大二在校生（昵称:莫凡）
• 我们在OpenHarmony成长计划啃论文俱乐部里，通过啃论文方式学习hash技术…
• 原文网盘链接: https://pan.baidu.com/s/1qfXyvZ1IsBlTakRcV04KmQ 提取码: 5kb4

---

---

随着信息存储和网络技术的迅速发展，每天从社交网络、业务交易、传感器等众多领域产生数以百万的字节的数据。日益增长的数据量对传统的数据分析工具在存储、处理和分析这些极其庞大的数据方面提出了重大挑战。几十年来，哈希一直是用来压缩数据，为了能够快速访问和分析，以及信息完整性验证的最有效工具之一。为了有效地进行哈希，哈希技术也从简单的随机化方法发展到考虑局部、结构、标签信息和数据安全的自适应方法。本调查将现有的哈希技术作为一个分类法进行回顾和分类，以及对不同类型的数据和应用提供主流哈希技术的全面视图。该分类学还研究了每种方法的独特性，因此可以作为理解不同哈希机制的生态位的技术参考，用于未来的发展。

类别和主题描述：A . 1 [介绍和调查]：哈希通用术语：设计、算法附加关键词和短语：哈希、压缩、降维、数据编码、密码哈希

1. 介绍

近年来信息系统的发展，包括存储设备和网络技术的进步，使得许多应用产生了大量的数据，需要大量存储、快速传递和快速分析。这样的现实对如何准确、高效地检索/比较数百万种不同数据类型的记录，如文本、图片、图形、软件等，提出了根本性的挑战。为了支持快速检索和验证，应用程序(如数据库系统)经常使用短消息‘键’来表示一个大表中的记录，这样用户就可以高效地从一个大的存储库中检索项目。

事实上，在收集数据进行存储或处理时，使用较少的信息来表示它们的意义。这激发了哈希技术，将数据记录转换为更短的定长值(固定长度)或桶地址，这些定长值或桶地址可以用大幅减少的运行时或存储消耗来表示原始数据。这样的转换可以通过使用哈希函数( )将原始数据记录映射到更低维空间来实现，条件是：( 1 )每个项在哈希空间中随机/策略性地映射到一个点，( 2 )两个值相同的项将产生相同的哈希值并映射到同一个点。借助哈希函数，可以在几乎恒定的时间内以$O(1)$的代价对数据进行插入、删除和查找等典型的数据访问操作。

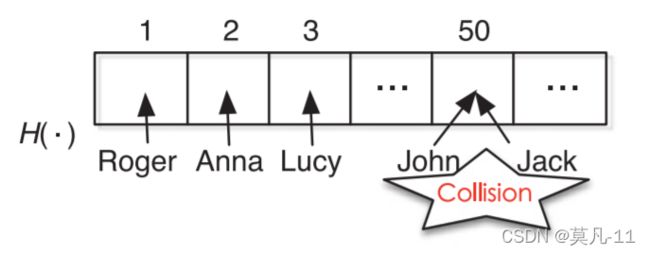图1 .一个哈希实例：每个字符串代表一个名称，数字代表哈希空间中对应每个字符串的哈希值的点。一个哈希函数h ( · )将每个黑字符串映射到相应的数字上。红色的“碰撞”表示两个不同的字符串映射到同一位置，因此发生碰撞。

当将每个记录映射到哈希空间时，不同值的数据记录可能具有相同的哈希输出，因此被映射到相同的位置并导致碰撞。如果数据记录多于哈希点，冲突不可避免，如图1所示。因此，哈希算法主要面临两个问题：( 1 )如何在高效的基础上设计更好的哈希函数来最小化碰撞或者提高精度；( 2 )当碰撞发生时，如何处理。

图1演示了为高效数据访问使用哈希的概念视图。一个哈希函数h ( · )将每个字符串映射为数值。在搜索记录时，可以对查询项进行哈希，并直接生成对应于该记录的哈希值。由于哈希值可以用恒定的时间计算，所以哈希可以以O ( 1 )的代价检索一个查询，这比通过所有记录( 通常服从 O ( n )或O ( logn )代价搜索n个记录 )要高效得多。

Hashing可以非常有利于许多应用，例如

1. text classification（文本分类）[Chi et al. 2014; Xu et al. 2011a]
2. image retrieval（图像检索）[Chum et al. 2008; Kulis and Grauman 2009; Torralba et al. 2008]
3. multimedia search（多媒体搜索）[ Zhu et al. 2013a, 2013b; Song 2015 ]
4. data verification（数据验证）[ FIPS 1995; Black et al. 1999; Breitinger et al. 2014; Hsieh 2004 ]

例如，在图像检索中，一个重要的挑战就是在内存消耗很少的情况下，开发高效的相似性度量和快速匹配方法。在现实中，图像数据库往往非常庞大，很难甚至不可能将所有的图像信息存储在内存中。另一方面，直接比较图像比较耗时。因此，从大型图像数据库中查找与查询示例相似的图像，是耗时的。在这种情况下，压缩数据有利于加快搜索过程。例如，二进制程序表示可以将原始特征空间中的相似点映射到哈希码空间中的附近二进制代码。哈希中的紧凑表示可以有效地节省存储，实现对大规模数据集的快速查询。此外，哈希还可以帮助验证大量数据是否被第三方修改，通过比较哈希消息代替原始数据，例如，验证软件是否被恶意修改为植物病毒代码[ Hsieh 2004 ]。

在使用哈希技术时，应用程序主要由两个截然不同的动机驱动：( 1 )如何从大量的数据集合中检索或比较项目 或( 2 )如何验证大量信息是否确实来自其所有者，并且没有第三方进行任何更改或修改。第一个动机是数据驱动，数据访问效率起着至关重要的作用。另一方面，第二个动机是安全驱动，具有数据验证的目的。尽管它们都使用哈希原理，但对数据或安全视角的关注往往导致不同的哈希技术和解决方案。面向数据的哈希通常采用两类方法，数据无关哈希和数据依赖哈希。如果哈希函数集是独立于要哈希的数据而定义的，而不涉及来自数据的一个训练过程，那么我们就参考了诸如数据无关哈希等方法。否则，它们被归为数据依赖的哈希。对于面向安全的哈希，它通常使用密码安全散列或密码不安全散列的方法，前者比后者具有更严格的安全属性。

许多哈希技术是为了不同的目的而存在的，实际的哈希机制因数据特性或底层应用程序的目标而异。然而，目前还没有一个全面的调查能够提供对主要哈希技术的 强弱以及不同类型哈希方法的生态位的完整看法。这样的限制使得设计新的哈希方法在技术上变得困难，特别是对于数据工程师或从业者。

在本调查中，我们将现有的哈希技术分为两个主要的层次分类：面向数据的哈希和面向安全的哈希。我们的调查将回顾 这两个层次的主流方法的独特性和强度，并总结涉及哈希的主要领域应用。从技术和应用的角度进行的联合审查提供了理论和实践的观点，因此，这项调查有助于激发新的哈希技术，并为实际实现提供技术参考。

调查内容安排如下。第2节简要介绍了哈希历史并定义了一些术语。第3节将哈希方法分类为一个层次分类。第4节审查了详细的哈希技术。第5节介绍哈希应用，我们在第6节中总结了这一调查。

---

2. 历史和初步准备

2.1 哈希简史

“哈希”一词源自物理世界，其中“哈希”的标准含义是“切碎搅拌”（chop and mix），直观地表示哈希函数“斩拌”信息并导出哈希结果。哈希技术的重要性从计算机系统的早期阶段就得到了很好的认识。1950年第一台真正的电子计算机发明后不久，哈希的概念在1953年首先被提及[ Luhn 1953 ]，在这里定义了一个使用随机密钥的一般哈希函数，可以达到等效于均匀分布随机变量的数学概念。在计算机科学中，要得到完全均匀分布几乎是不可能的。创建均匀分布只能通过考虑密钥的结构来实现。对于任意一组密钥，由于无法事先获得密钥，因此也不可能创建一个性能更好的通用哈希函数。在这种情况下，随机均匀哈希是最好的。

1957年，出于使用业务应用容量非常大的随机访问系统的需要，Peterson [1957] 提供了大量搜索的方法，为了能够在几类存储系统中 准确定位一条记录，包括包括索引表方法和排序文件方法。1968年，“哈希”一词首次被使用[ Morris1968 ]。

2.2. 定义

2.2.1 定义 哈希函数（Hashing function）

哈希函数是任何函数$h(\ast )$，可以用来将任意大小的数据映射到固定的区间$[0，m]$。给定一个包含n个数据点$X=[x1,x2,...xn]\in R^D$的数据集和一个哈希函数$h(\ast )$，则$h(X)=[(x1),(x2),...,(xn)]\in [0,m]$可称为数据点$X=[x1,x2,...xn]\in R^D$的哈希值或简单的哈希。

哈希函数的一个实际用途是一种称为哈希表的数据结构，它已被广泛应用于快速数据查找。

2.2.2 定义 最近邻 (NN) (Nearest neighbor (NN))

给定一组n个数据点$X=[x1,x2,...xn]\in R^D$，$NN$表示$X$中最接近查询点$x_q$的一个或多个数据项。

2.2.3 定义 近似最近邻 (Approximate nearest neighbor (ANN))

给定一组$n$个数据点$X=[x1,x2,...xn]\in RD$，$ANN$打算寻找一个数据点$x_a\in X$，即查询点$x_q$的ε-近似最近邻，对于所有的$x_a\in X$，$x_a$ 与 $x$的距离满足 $d(x_a,x)\le (1+\epsilon )d(x_q,x)$。

---

3. 哈希技术分类

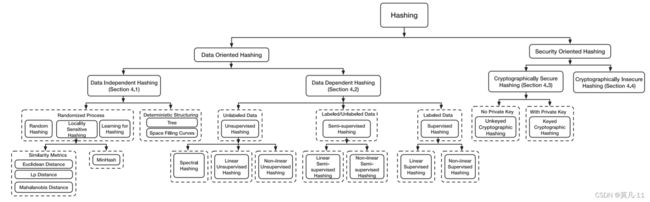图2.哈希技术的层次分类法。Hash方法分为两类：面向数据的Hash方法和面向安全的Hash方法。每个小组包括两个小组，其内容在各自的小节中审查。

在图2中，我们分别从数据和面向安全的角度将哈希技术归类为一个层次分类。从面向数据的角度来看，哈希主要用于加快数据检索过程，通过使用数据无关的哈希或数据依赖的哈希。从面向安全的角度来看，哈希作为消息摘要器产生签名进行验证，其中数据安全是首要关注的问题。面向安全的哈希也有两种主要类型，密码学上的不安全哈希和密码学上的安全哈希，考虑到某些安全属性是否得到保证，如collision resistance or preimage resistance（碰撞抵抗或原像抵抗）[ Menezes et al 1996年 ]。

---

3.1 面向数据的哈希（Data-Oriented Hashing）

面向数据哈希是指打算使用哈希来加快数据检索或比较的方法，其中哈希表通常是为了查询而维护的。

3.1.1 数据无关哈希（Data-Independent Hashing）

如果一个哈希函数是独立于要处理的数据而定义的，而不涉及来自数据的训练过程，那么我们将这种哈希技术称为数据无关哈希。一个数据无关的哈希方法没有任何标记的数据/信息来帮助评估哈希结果的质量。哈希函数通常是预先指定的，尽管其中一些函数可以学习数据分布以改进哈希结果，例如对局部性敏感的哈希或学习哈希。与数据无关的哈希函数根据底层投影模式可分为四类：随机投影、局部性敏感投影、哈希学习和结构化投影。

3.1.2 数据依赖哈希（Data-Dependent Hashing）

基于数据的哈希学习是在给定一组训练数据的基础上学习哈希函数，使得哈希函数能够为所有数据记录找到最佳的紧致码。由于数据依赖的哈希结果对底层数据高度敏感，因此伴随着更快的查询时间和更少的内存消耗。为了更好地保存局部信息并实现更好的选择性，数据依赖的哈希需要通过为给定的训练数据集唯一定义哈希函数族来紧密地拟合特征空间中的数据分布。此外，数据依赖哈希通常考虑比较与训练数据中特征的相似性。
根据训练数据中标签信息的可获得性，数据依赖哈希方法分为无监督哈希、半监督哈希和监督哈希3大类。
标签提供了有价值的信息来揭示每个实例的语义分类( 或实例之间的相关性 )。这些标签提供了与每个实例的特征值相比较的额外信息，以便找到适合训练数据的良好哈希函数。此外，即使每个实例的实际标记未知，也可以指定弱标记或部分标记信息，如成对标记，以指示某些实例之间是否接近( 例如 ,属于同一群体 )。这样的弱标签信息对设计哈希函数也非常有帮助。这类方法通常被称为半监督哈希。另一方面，如果根本没有提供标签信息进行训练，我们将这类哈希称为无监督哈希。

3.2 面向安全的哈希（Security-Oriented Hashing）

面向安全的哈希是指用于验证或确认的哈希方法。例如，用户可能会从公共Web服务器下载软件，但担心软件是否被第三方修改。为了验证目的，软件所有者可以发布软件的MD5 [ Rivest 1992 ]哈希代码。用户可以从不同来源下载软件并生成新的MD5代码。如果两个MD5代码完全相同，就意味着下载的拷贝是原始的，软件没有改变。由于MD5代码相对较小( 例如 128位 )，比比较几百兆的原始数据要容易得多。同时，由于面向安全的哈希代码往往比面向数据的哈希代码长得多，所以通常不需要或无法维护哈希表。该类中的方法主要关注安全属性。由于这样的原因，与面向数据的哈希方法相比，它们往往计算代价高，效率低。

3.2.1 加密安全的哈希（Cryptographically Secure Hashing）

加密安全哈希，或简称加密哈希，是指那些哈希函数设计为单向且非常困难(如果不是不可行的话)的方法来进行可逆。在应用这种方法时，输入长度( 又称‘消息’。)是任意的，输出大小(也称"消息摘要" )是固定的。固定大小的哈希结果被用作签名来表示用于验证的原始消息。由于这种安全敏感的性质，密码哈希具有严格的雪崩效应，这就要求如果输入发生了变化( 例如 ,在输入中改变一个单比特 )，一个哈希输出发生明显变化( 例如 ,大约一半的输出比特发生变化 )。

对于加密哈希，通常强制三个属性：( 1 )原像抵抗（preimage
resistance），( 2 )第二原像抵抗（second preimage resistance），( 3 )碰撞抵抗（collision resistance）。原像抵抗意味着如果仅知道输出(消息摘要) ( 即单向属性 )，输入(消息)很难找到。第二个原像抵抗是指给定消息$m_i$及其哈希输出$hash(k,m_i)$，其中k是哈希密钥，很难找到另一个满足$hash(k,m_i)=hash(k,m_j)$ ( 也就是说 ,第二原像攻击 )的消息$m_j$。抗碰撞要求两个消息$m_i$和$m_j$具有不同的哈希结果，以避免 a birthday attack(即攻击者可以找到两个具有相同哈希输出的输入消息)。

3.2.2 加密不安全的哈希（Cryptographically Insecure Hashing）

虽然加密安全哈希具有很好的安全属性，但它们往往计算效率不高。对于没有强烈安全关注度的应用，一种更简单的哈希机制，称为加密不安全哈希或非加密哈希，更具有实用性。对于非加密哈希，如:Fowler-Noll-V ( FNV )哈希函数[ Fowler 1991 ]，主要目标仍然是生成哈希输出进行验证，但哈希过程不必考虑密码学。因此，与加密安全哈希方法相比，它具有更快的处理速度、更低的碰撞概率、更高的检测小错误的概率和更容易的碰撞检测。这种哈希方法在需要快速搜索或处理的应用程序中尤其流行，例如Twitter、域名服务( DNS )服务器或数据库实现。

---

4. 哈希技术描述

在这一部分中，我们首先回顾了面向数据和面向安全的哈希方法，将它们分为四个小节，如图2所示。之后，我们将总结所有四类方法的时间复杂度。

4.1 Data-Independent Hashing Methods

下面我们首先介绍最简单的投影方法——随机投影，然后推进到局部性敏感投影，以保存数据的局部性特征。之后，我们将进一步引入学习哈希投影和结构化投影。哈希算法类别见表Ⅰ。

Table I. Categorization of Data-Independent Hashing Methods

Random Hashing	Random Projection Hashing; Universal Hashing
Locality Sensitive Hashing
	Locality-Sensitive Hashing (LSH)
	MinHash; Weighted MinHash (WMH)
	Shift-Invariant Kernel-Based Hashing (SIKH)
	Nested Subtree Hashing (NSH)
	Discriminative Clique Hashing (DICH)
Learning for Hashing	BoostMap
Structured Projection	Quadtree; Hilbert Curve; Z curve

4.1.1 Random Hashing

随机投影哈希是一种通用的数据约简技术，它将原始高维数据随机投影到低维子空间中。例如，一个具有d维特征的原始数据项经过随机投影哈希后可以投影到k维($k\ll d$)子空间。

随机投影哈希最早提出[ Donald 1999 ]，利用一个随机函数h：$U\to V$在域V (对应于k维数据)中一个随机哈希值$h(x)$，并与原域U ( 与 d维数据对应 )中的数据项关联。在随机投影中，一个随机函数需要$d\times lgk$位来表示，从而导致存储一个随机选择的函数的不可行性。据此，一些研究者开始在随机投影中使用固定函数。Carter和Wegman 提出了一种通用哈希方法，该方法从一个小函数族中随机选择哈希函数，而不是从所有函数中随机选择哈希函数。从而保证了可证明性能，实现了哈希函数的可行、简洁存储。例如，Shakhnarovich [2005]提出了一种任务特定的相似性度量来从哈希函数族F中统一选择哈希函数：
$$\left\{x⟶((ax+b)modp)modv|0<a<p,0\le b<p\right\}$$
整个家族由参数p和v定义，特定的哈希函数由参数a和b定义。
在这种通用哈希中，U中的每一组n个元素统一投影为随机独立的值，对应的族F是n向独立的。Wegman 和 Carter [1981] 提出了这类函数族，其中一个随机函数需要$nlgd$比特的空间来存储。在相当长的一段时间内，所有睿智独立的族用来评估哈希函数的时间复杂度为$O(n)$。然而，Siegel [2004] 的一个重要突破提出了极端随机的恒定时间散列函数（extremely random constant-time hash functions），其中散列族相对较小且高度独立，因此可以在恒定时间内对其进行评估。

尽管随机投影技术简单，计算效率高，但其主要缺点是高度不稳定性。换句话说，不同的随机哈希函数可能导致完全不同的哈希值。另一方面，如果两个元素在一个比特上有差异，它们将有两个不同的哈希值，并被投影到两个完全不同的随机点上。因此，纯粹基于随机投影的哈希固有地丢弃了原始特征空间的特性，对于某些应用无法取得良好的性能。为了保存原始特征空间中的数据特征，引入了局部性敏感哈希。

4.1.2 Locality-Sensitive Hashing

最常见的与数据无关的随机投影方法是局部敏感哈希( LSH ) [ Indyk和Motwani 1998；Gionis等人1999 ]。由于它的广泛普及，我们简要介绍这种具有代表性的方法，以及它的优缺点。

LSH：给定一个包含n个数据点/项$X=[x_1,x_2,...x_n]\in R^D$的数据集和包含K个哈希函数的哈希函数$H(\ast )$，LSH将一个数据点$x_i$映射到一个K位哈希码$\in${0, 1}：
$$H(x_i)=[h_1(x_i),h_2(x_i),...,h_k(x_i)]$$
LSH的一个重要特点是距离较小的两个数据点，在原始特征空间中，更可能有类似的哈希码。换句话说，在Hamming空间中，LSH很大程度上保留了原始的局部信息。这样的局部保持性质可以用下列方程在两个数据点x和y之间进行阐述：
$$P\left\{H(x)=H(y)\right\}=sim(x,y)$$
其中$sim(x,y)$是相似性度量，可以用距离函数表示，如：p范数(p-norm)距离($p\in (0,2]$) [ Datar等 . 2004年 ]、马氏距离(Mahalanobis distance)[ Shakhnarovich 2005 ]、角相似性(angular similarity)[ 查里卡尔 2002年；Ji等。 2012 ] 和核相似性(kernel similarity)[ Kulis和 Grauman 2009 ]。对于随机投影散列，LSH有
$$H(x)=sign(w^{T}x+b)$$
其中w从几何角度表示随机超平面，b表示随机截距。每个数据点的标记由超平面w的边决定。因此，LSH满足
$$H(x)=\{\begin{array}{cc}0& if(w^{T}x<b)\\ 1& otherwise\end{array}$$
具体地，基于此哈希函数，对于任意两点$x，y\in R^D$，LSH满足
$$P\left\{h_m(x)=h_m(y)\right\}=1-\frac{1}{\pi }{\cos }^{-1}(x^{T}y)$$
LSH不仅保存了哈希空间中的数据特征，而且保证了相似数据点之间的碰撞概率。尽管LSH具有不可忽视的优点，但它仍然存在一个不可回避的缺点，那就是哈希码的低效性。首先，LSH中哈希函数的随机生成和数据的独立性不能保证效率。第二，LSH在每个哈希表中通常需要较长的代码才能保证一个可以接受的精度，这就增加了查找的复杂度。根据方程上述公式，碰撞概率随码长呈指数递减，因此LSH在满足渐近理论性质的前提下，需要长二进制码才能达到较好的精度，这也导致在创建哈希查找表时召回率较低。因此，最近的一些研究工作集中在生成短紧凑型哈希码上。在所有这些努力中，数据依赖哈希得到了显著的注意点( 我们很快将在第 4.2节中审查 )。

借助简单的随机投影，距离较小的两个对象更可能拥有相同的LSH哈希码。对于LSH中的相似性度量，有很多方法[ Datar等。2004；Shakhnarovich 2005；恰里卡尔 2002；库利斯和格劳曼2009；Ji等。2012 ] 使用p范数对$p\in (1,2]$ [ Datar等 . 2004年 ]，马氏距离[ Shakhnarovich 2005 ]，角相似度[ 恰里卡尔 2002 ; Ji等。 2012年 ]，核相似度[ 2009年 Kulis和 格劳曼 ]。LSH的基本思想是首先选择一个随机超平面，然后利用该超平面对输入向量进行哈希。超平面常被用来将数据点划分成两个集合，两个不同的二进制码会根据这个集合分配给每个数据点。对于超平面，为了优化分配每一个LSH超平面的可变比特数，Moran等人[ 2013a , 2013b ]提出了称为邻域保持量化( NPQ ) [ Moran等人 2013a ]和称为可变比特量化( VBQ ) [ Moran等人。2013B ]。前者基于自适应学习阈值为每个超平面分配多个比特，后者提供了数据驱动的跨超平面非均匀比特分配。基于LSH的随机投影，Zhang等人 [2013] 提出了分发意识LSH ( DALSH )，它使用数据自适应投影来解决对真实数据缺乏适应的问题。

MinHash，又称min-wise独立排列局部性敏感哈希方案，是另一种LSH相关哈希技术，常用于文本挖掘或需要快速评估两组之间相似度的应用程序[ Broder1997；Bharat和Broder1998 ]。最小哈希可以有效地估计两个集合$S_1$和$S_2$之间的相似度，每个集合包含多个元素( 例如 ,使用共享关键词查找两个文档之间的相似度 )。为了发现$S_1$和$S_2$之间的相似性，分别对$S_1$和$S_2$中的元素应用K个哈希函数(随机排列)。$S_1$，$S_2$的最小哈希值为$S_1$，$S_2$的最小哈希。通过检查两个集合之间的最小哈希值，可以快速评估$S_1$和$S_2$之间的相似性，而不需要涉及复杂的集合运算来检查它们的成员关系，如下列公式所定义：
$$\hat{\mathrm{J}}\left(S_1,S_2\right)=\frac{{\sum }_{k=1}^{K}1\left({\hslash }_k\left(S_1\right)={\hslash }_k\left(S_2\right)\right)}{K}$$
$where1\left({\hslash }_k\left(S_1\right)={\hslash }_k\left(S_2\right)\right)=1if{\hslash }_k\left(S_1\right)={\hslash }_k\left(S_2\right)$ , and $1\left({\hslash }_k\left(S_1\right)={\hslash }_k\left(S_2\right)\right)=0$ 即如果相等，则值为1反之值为0。
$otherwise.AsK\to \infty ,\hat{ȷ}\left(S_1,S_2\right)\to \mathrm{J}\left(S_1,S_2\right)$

除了计算效率外，最小哈希还具有非常好的性质：如下方公式所示，$S_1$和$S_2$可以哈希到相同的最小哈希值的概率等于$S_1$，$S_2$的Jaccard相似系数。也就是说，如果使用了足够多的置换，基于最小哈希的相似系数就相当于常用的集合相似性度量Jaccard相似系数：
$$\mathrm{Pr}\left(\hslash \left(S_1\right)=\hslash \left(S_2\right)\right)=\frac{\left|S_1\cap S_2\right|}{\left|S_1\cup S_2\right|}=\mathrm{J}\left(S_1,S_2\right)$$
在图3中，我们演示了一个Min-wise散列过程的例子。给定两个集合$S_1=$ { 1，2，4，7 }和$S_2=$ { 3，4，7 }，以及两个独立的随机元素置换$h_1=[2,5,7,6,4,3,1]$和$h_2=[7,3,1,2,5,4,6]$，对于集合$S_1$，最小$h_1$散列值为2，最小$h_2$散列值为7。对于集合$S_2$，最小 $h_1$哈希值为7，最小 $h_2$哈希值为7。因此，$S_1$和$S_2$的相似度为1 / 2。

图3. 最小哈希过程的一个例子：在表的最后两列中，"1"或"0"表示相应元素在集合(S ₁或S ₂)中或不在；h ₁和h ₂表示两个不同的哈希函数。

Min-wise散列方案最初是在Broder[1997]中提出的，后来被用于从 AltaVista 搜索引擎[ Bharat和 Broder 1998 ]、大规模文档聚类[ Broder 1997 ]、近重复图像检测[ Chum等人 2008年 ]和大规模文本分类[ Chi等 . 2014 ]中检测和消除重复网页，使用递归Min-wise散列 ( RMH )保存上下文信息。同样，通常使用另一种称为SimHash [ Sadowski和 Levin 2007 ]的相似哈希函数来确定文件相似度。为了将MinHash与SimHash进行比较，Shrivastava 和 Li [ 2014c ]提供了第一种在不同相似性度量下进行比较的可证明方法，并验证了MinHash即使在 cosine相似性 上也优于SimHash。

尽管MinHash被验证是一种高效的哈希方法，但仍有很大的改进空间。为了节省存储空间，Li等人提出，Li和Konig [ 2010、 2011年 ]，以及Li等人。将最小哈希技术扩展到 b-bit Min-wise散列，改变了传统的64位Min-wise散列方法中存储每个哈希值的方法。为了使Min-wise散列更快，Shrivastava and Li [ 2014a , 2014b ]利用排列和致密化的思想，相对于Min-wise散列提供了大量的计算开销节省。Manasse等人[2010]从另一个角度受到加权抽样的启发。Ioffe [2010] 和 Shrivastava [2016] 逐渐提出了一种 Weighted Minwise Hsahing（WMH），并验证了WMH更简单、更快、更高效的记忆。

另一种随机投影哈希技术包括 Shift Invariant Kernel-Based Hashing( SIKH ) [ Shakhnarovich 2005 ; Raginsky和 Lazebnik 2009 ]，Nested Subtree Hashing ( NSH ) [ Li等 . 2012年 ]和 Discriminative Clique Hashing ( Dich ) [ Chi等 . 2013年 ]。Shakhnarovich [2005] 和Raginsky和Lazebnik [2009] 基于随机投影，提出了一种简单的无分布编码方案，该方案可以将两个向量对应的两组二进制码之间的the expected Hamming distance 与两个向量之间的 a shift-invariant kernel 的值联系起来。对于涉及动态增加的网络数据的数据挖掘应用，Li等人和Chi等人 提出了新的哈希方案，以解决流上的大规模图分类问题。在Li等人那里，我们提出NSH从图流中提取多分辨率子树模式，并将每个模式哈希到低维特征空间。在Chi等人那里，采用两种随机哈希方案加快团模式挖掘过程，解决无限团模式扩展问题。

4.1.3 Learning for Hashing

哈希学习是针对给定数据学习新的哈希空间的一组数据敏感的哈希方法。Shakhnarovich等人 提出了BoostMap，一种用于欧氏嵌入构造（Euclidean embedding construction）的与数据无关的机器学习方法。

BoostMap计划为底层数据指定的每个任务学习一个新的嵌入空间，因此新的哈希空间能够最优地揭示数据的相似性。它是一种有效的近似最近邻方法，可用于任意距离测度、度量或非度量。在介绍BoostMap之前，我们首先介绍了构造 欧氏嵌入的一些基本方法，如Lipschitz嵌入[ Johnson and Lindenstrauss 1984 ]，Bourgain嵌入[ Hjaltason和Samet 2003；Bourgain 1985 ]、FastMap [ Faloutsos 和 Lin 1995 ]、MetricMap [ Wang等人。2000年 ]和Boostmap [ Shakhnarovich等 . 2006年 ]。

1、Lipschitz嵌入的基本思想是将度量空间嵌入到其他低失真空间中。在Lipschitz嵌入中，一个对象$x\in X$(a space)被转化为一个n维向量$V=(v1,v2,\dots ,vn)$，使得每个元素$v_i$对应于对象$o\in X$到预定义参考集[ Hjaltason和 Samet 2003 ]的距离. Bourgain嵌入是Lipschitz嵌入的一种特殊类型。
方程$P_o(x)=D_X(x,o)$可以表示空间X中的 一维 欧几里得 嵌入$P_o$，对象o称为参考对象。如果$D_x$服从三角形不等式，则$P_o$将X中的附近点直观地映射到实线R上的附近点。即使$D_x$违反了三角形不等式，X中的邻近点仍可能被$P_o$ [ Athitsos和 Sclaroff 2003 ]映射到R中的邻近点。另一方面，距离较远的点也有可能被映射到附近的点。

2、在FastMap中，基本思想是选择两个数据对象$x_1,x_2\in X$作为枢轴对象，然后定义任意x的嵌入$P^{x1，x2}$为x在x1和x2之间的直线上的投影。FastMap分别根据x和x1之间以及x和x2之间的距离定义投影。然后将距离处理为三角形的边：
$$P^{x_1,x_2}(x)=\frac{D_X{\left(x,x_1\right)}^2+D_X{\left(x_1,x_2\right)}^2-D_X{\left(x,x_2\right)}^2}{2D_X\left(x_1,x_2\right)}$$
图4演示了上述公式中使用的FastMap投影的示例。在上述公式中，$P^{x1,x2}$将原始空间中相互接近的数据对象投影到附近的位置，并保持数据对象的邻近结构。在FastMap中，多个对支点对象被用来投影有限组数据对象。

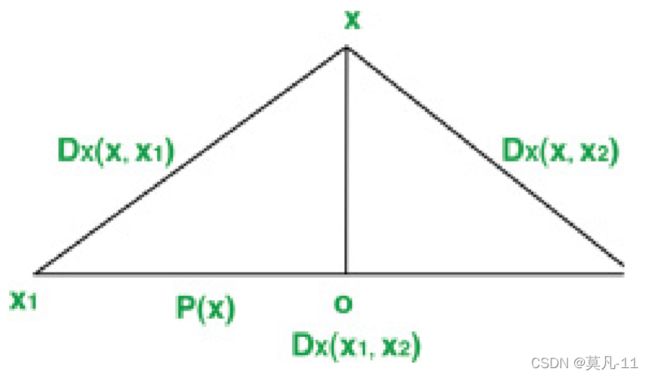图4.上述公式中使用FastMap投影的例子。边长xx ₁、xx ₂、x ₁x ₂分别为D _X(x, x ₁ )、D _X (x, x ₂)、D _X (x ₁ , x ₂ )。一条从x出发的线x _o垂直于x ₁x ₂，线段x1 _o的长度等于P ^x1，x2( x )。

3、MetricMap [ Wang等人。 2000年 ]扩展了FastMap，将有限数据对象映射到伪欧氏(pseudo-Euclidean)空间上，在使用非欧氏(non-Euclidean)空间时优于FastMap。

4、BoostMap [ Shakhnarovich等。2006年 ]优化了量化测度，比使用随机选择和启发式方法保存更好的相似度排序。同时，BoostMap的学习是独立的，不需要原始的距离度量，如欧式或度量属性。BoostMap中学习过程的关键是将嵌入作为分类器来估计任意三个数据对象的距离，并使用AdaBoost [ Schapire和 Singer 1999 ]将之前所有的低维嵌入合并到一个高维嵌入中进行更高精度的相似度排序。
BoostMap的主要过程如下：在基于一对枢轴对象或一个参考对象识别出一大类1D嵌入P后，每个P被处理为连续输出的二进制分类器和弱分类器[ Schapire 和 Singer 1999 ]。之后，BoostMap使用AdaBoost将一维嵌入P合并到多维嵌入中，作为一个强分类器，其准确率相对于弱分类器更高。BoostMap充分利用机器学习技术的优势，从众多的一维嵌入中组装出更高精度的嵌入。

4.1.4 Structured Projection

许多哈希方法都存在，但它们主要对低维数据有效。当将这些方法应用于高维(或非常高维)数据时，它们的性能可能会下降。对于高维向量空间( HDVS )中的相似性搜索，传统的方法是采用多维索引结构，需要对数据空间进行划分。
结构化投影哈希方法表示一组沿预定义行划分数据空间的方法，不管数据特征如何，其中不同的哈希方法定义了它们唯一的行划分结构。例如，Weber et al. [1998], Joly et al. [2004], and Poullot et al. [2007] 提出了具有结构化投影的数据无关哈希方案，包括 tree[ 韦伯等人 1998年 ]和space-filling curves[ Joly et al. 2004 and Poullot et al. 2007 ]。
Weber等人研究了维数对HDVS最近邻相似度搜索的影响，证明了在维数足够高的情况下，任何划分方案和聚类技术都必须退化为遍历所有块的顺序扫描。本文采用了一些树状结构对数据空间进行划分，他们的结果表明，对于高维数据，基于树状结构比顺序扫描的性能提高了一个数量级。一个实例如图5 ( a )所示，它采用了基于四叉树(树数据结构)的数据空间划分。在四叉树中，每个内部节点恰有四个子节点或者没有子节点。它主要用于递归地将二维空间划分为四个象限或区域。在图5 ( a )的右侧面板中，空间被划分为四个象限，节点0位于中心。平面一侧的节点1形成一个区域，另一侧的节点2、3和4形成另一个区域。以这种方式使用平面，递归分区空间生成显示在图5 ( a )左侧面板上的树。

图5 ( a )树中的每个节点表示一个包围矩形( 在右分裂矩形中 )，复盖整个空间的一部分；根节点' 0 '代表整个空间；阴影区域表示左树中节点‘5，‘8，‘9，’和‘12’对应的哈希前缀或范围。( b )绿线说明一个Hilbert曲线‘访问’每个四边形的顺序。( c )：绿线表示哈希方法"访问"每个四元组的顺序。

Joly等人和普洛等人 研究了基于内容的空间填充曲线投影拷贝识别方法。具体而言，Joly等人的文献提出了一种适用于基于内容的副本识别的伪不变特征检索新策略。他们采用希伯特曲线作为投影线，直接将近似搜索范围映射到希尔伯特空间填充曲线上，以便建立对数据库的有效访问。希尔伯特曲线的优点是可以保证索引中相邻的两个单元格也是描述空间中的邻居[ Jagadish 1997 ]。
图5 ( b )展示了利用希尔伯特曲线在深度3 (左)和4(右)进行的二维数据空间划分。在图5 ( b ) (左)中，希尔伯特曲线复制在四个象限$R_0、R_1、R_2和R_3$。复制过程中，象限$R_0$顺时针旋转90°，象限$R_3$逆时针旋转90°。旋转后，两个下象限$R_0、R_3$的感觉均发生反转。两个上象限R1，R2不会旋转。根据这一规律，可以得到深度为4的Hilbert曲线。所有的旋转和感觉计算都是相对于先前获得的旋转和感觉在一个特定象限。图5 ( b ) (左)显示了2 * 2网格的基本Hilbert曲线。推导出这条曲线更深的深度的过程是在R0和R3处旋转和反射曲线。通过在基本曲线的每个顶点处遵循相同的旋转和反射模式，曲线可以保持递归增长。图5 ( b )分别给出了深度为3和4的Hilbert曲线。
对于Hilbert曲线，一个缺点是难以从描述空间中的位置开始计算索引中的键，用于高维空间和高阶划分。为了简化密钥( 索引中的单元格地址 )的计算，并将其紧密地链接到组件式搜索过程中，Poullot等人提出了一种新的方法。使用Z空间填充曲线替换Hilbert曲线，并按照Z曲线将描述空间分层划分为超矩形网络单元格，如图5 ( c )所示。Z曲线在空间划分方面的优势是显而易见的：无论深度如何，所有单元格都是沿着相同的维度进行划分的。

---

4.2 Data-Dependent Hashing Methods

基于数据的哈希可分为三类：无监督哈希、半监督哈希和有监督哈希。

---

4.2.1 Unsupervised Hashing

对于无监督哈希，不提供标签信息，包括弱标签，例如实例间的成对标签。无监督哈希方法使用未标记数据为给定的训练数据生成二进制代码，并试图在原始特征空间中保存相似信息。

根据哈希所用函数的实际形式，包括特征函数、线性函数和非线性函数，我们将无监督哈希方法分为三类：谱哈希、线性哈希和非线性哈希。分类和一些重要算法概述在表二。

Table II. Categorization of Unsupervised Hashing Methods

Unsupervised Hashing	Spectral Hashing
	Linear Unsupervised Hashing	Anchor Graph Hashing (AGH)
		Product Quantization (PQ)
		Angular Quantization-Based Binary Coding (AQBC)
		Spherical Hashing
		Isotropic Hashing
		Manhattan Hashing
		Predictable Dual-View Hashing (PDH)
		Inductive Manifold Hashing (IMH)
		Locally Linear Hashing (LLH)
		Topology Preserving Hashing (TPH)
	Nonlinear Unsupervised Hashing	Kernelized LSH (KLSH)
		Multiple Feature Kernel Hashing (MFKH)

光谱散列。谱哈希( SH ) [ Weiss等 . 2009年 ]是最流行的依赖于数据的非监督哈希方法之一。许多方法使用谱哈希来解决带语义的哈希代码学习问题。例如，Salakhutdinov 和 Hinton 提出了在哈希码的汉明距离较短的文档语义相似的情况下，为大量文档设计紧凑的二进制编码。Weiss等. 定义了一个与图划分相关的好代码的硬准则。

由于谱散列的流行，我们现在介绍它的详细过程。$SH$中学习紧凑代码的一般过程如图6所示，其中左边的列表表示一组数据点。通过使用哈希函数$H(x)$，可以学习每个数据点对应的压缩代码。之后，利用哈希表中的逆查找得到NN列表。因此，谱哈希不仅在缩小的Hamming空间中保持样本的相似性，而且寻找相似数据点之间的平均Hamming距离最小的样本。

图6学习紧凑代码的过程。

谱哈希假设输入是嵌入在$R^D$，$A_{ij}=exp(-\parallel x_i-x_j{\parallel }^2/{ϵ}_2)$。$A_{i,j}$是输入空间中一对数据点$(x_i,x_j)$之间的相似度。参数定义了$R^D$中的距离，该距离对应于类似的项。基于这些设置，相似邻居间的平均汉明距离为${\sum }_{ij}{A}_{ij}\parallel y_i-y_j{\parallel }^2$。

因此，谱哈希码满足以下标准[ Weiss等 . 2009年 ]：
$$Minimize:\frac{1}{2}\sum _{ij}{A}_{ij}{\Vert y_i-y_j\Vert }^2=\mathrm{tr}({\mathrm{y}}^{\mathrm{T}}Ly)$$
$$Subjectto:(1)y\in \{-1,1{\}}^{n\ast K};(2)1^T\mathrm{y}=0;(3)\frac{1}{n}{y}^{T}y=I_{K\ast K},$$
其中L是图Laplancian diag$(A1)-A$，约束$1^{T}y=0$定义了要平衡的比特，约束$\frac{1}{n}{y}^{T}y=I_{k\ast k}$定义了不相关的比特。

谱哈希包括训练和哈希三个主要步骤：( 1 )在n个数据点上建立精确邻域图的稀疏亲和矩阵A；( 2 )计算并二值化图LaplacianL的K个特征向量；( 3 )将K个特征向量推广到测试数据点上并二值化。

总之，谱散列对训练数据执行 主成分分析( PCA )，并拟合多维矩形。尽管它很简单，但实际上它是有效的，可以与许多先进的哈希方法媲美。但它的训练过程对于离线是难以处理的，而哈希过程对于在线是不可行的。

为了评估谱哈希结果，哈希的质量通常采用以下标准[ Salakhutdinov和 Hinton 2009 ]进行评估：( 1 )对一个新的输入容易计算，( 2 )需要较小的比特数对全数据集进行编码，( 3 )具有相似二进制码字的相似数据点。

由于获取监督信息往往是一个耗时的过程，作为一种公认的非监督码字生成方法，谱哈希最小化相似点之间的码字距离来学习短的二进制码字。虽然通过谱图划分方法学习二进制编码，谱哈希表现出了良好的性能，但随着比特数的增加，其性能可能会变差，用欧氏距离构造图拉普拉斯可能不能反映数据的内在分布。同时，虽然对训练数据中的输入进行计算是很简单的，但对于先前看不到的数据计算哈希码字是一个问题。

为了解决这些问题，很多方法存在扩展频谱哈希以解决特定挑战。针对示例，提出了多维谱Hashing ( MSH ) [ Weiss等 . 2012年 ]以保证性能的稳定性。MSH试图重建数据点之间的亲和力，而不是距离。为了反映数据的潜在分布，Li等人提出了一种基于图像标签/标签两两相似性直接优化图拉普拉斯的方法，该方法可以在优化过程中自动确定尺度因子。为了计算以前看不到的数据点的哈希码字，Bodo和Csat ´o 提出使用线性标量产品作为相似性度量，使用不同的泛化(一个归纳生成公式)来查找哈希码。由于推广，对于一个新的数据点，代码字生成方法和基于随机超平面的LSH方法是相似的。

线性无监督哈希。线性无监督哈希是指一组哈希函数为线性函数的方法，尽管算法可能依赖于基于学习的方法来推导实际的哈希函数。这些哈希算法大多侧重于挖掘数据亲和矩阵的光谱属性进行二进制编码。其中，锚图哈希( Anchor Graph Hashing，AGH ) [ Liu等人。 2011年 ]是一种流行的方法。作为一种基于图的哈希方法，AHG通过自动发现数据中的邻域结构来学习合适的紧凑代码。

下面我们简要描述锚图哈希方法：
AGH：为了使散列在计算上是可行的，AGH利用锚图来获得可牵引、非负、稀疏、低秩的亲和矩阵。锚点可以看作K均值聚类中心，当锚点数量足够多时，锚图可以近似精确的邻域图。

图7.矩阵Z和矩阵A：数据点之间的直线表示数据点之间的距离。

AGH首先计算数据到锚点的相似度，得到数据到锚点的相似度矩阵$Z\in R^{n\ast m}$( n个数据点 , m个锚点 )。基于$Z$，可以得到数据到数据的相似度矩阵$\hat{A}\in R^{n\ast n}$。其过程如图7所示，其中红色数据点为锚点，$\widehat{A_{ij}}={\sum }_{k=1}^m{Z}_{ik}{Z}_{jk}=Z_i{Z}_j^T$。因此锚图亲和矩阵$hatA=Z{\wedge }^{-1}Z(\wedge =diag(Z^{T}1)\in R^{m\ast m})$，不同于谱哈希中的亲和矩阵A。

AGH通过最小化寻找数据库中n个数据点的K位Hamming嵌入$y\in {1,-1}^{n\ast K}$
$$max:tr(y^T\hat{A}y)$$
$$Subjectto:(1)1^{T}y=0；(2)y^{T}y=n{I}_{K\ast K}$$
综上所述，AGH有5个主要步骤，包括训练( 步骤 1、 2和 3 )和哈希( 步骤 4和 5 )：( 1 )构建锚图并在n个数据点上获得数据到锚的相似矩阵Z，( 2 )计算并二值化锚图Laplacian的K个特征向量，( 3 )构建哈希表，( 4 )将K个特征向量泛化到测试数据点并二值化，( 5 )在哈希表中进行逆查找。

AGH是一种可扩展的基于图的无监督哈希方法，它考虑数据的底层流形结构来搜索最近邻。AGH通过向特征函数外推锚图拉普拉斯特征向量来保证线性训练时间和恒定哈希时间。在AGH中，r锚图拉普拉斯特征向量被用来生成r位码，对应于较高的图拉普拉斯特征值的较高特征向量的划分质量较低。为了解决这个问题，AGH使用两层哈希重访下层图Laplacian特征向量生成多个哈希位。

为了提高哈希性能，许多现有的方法都提出使用大量的哈希表(长码字)，造成了巨大的空间开销。针对这一问题，提出了一些解决方案。Lu等人 考虑了一种硬件友好的最小完美哈希( MPH )方案，该方案通过计数Bloom滤波器将内存访问次数减少到$O(1)$，并且仍然保持空间高效。为了进行性价比高且精确的模式匹配，HashMem [ Kontak等人 2012年 ]提出将哈希和内存结合起来，利用哈希为存储在内存中的每个候选模式生成一个截然不同的地址。Lin等人结合稀疏编码和压缩感知技术，发展了一种用于高维近邻搜索的哈希算法压缩哈希( CH )。

其他重要的线性无监督哈希方法包括针对视觉和文本应用中普遍存在的高维非负数据的ANN搜索算法产品量化( PQ ) [ Jegou等人 2011年 ]和基于角量化的二进制编码( AQBC ) [ 龚等人 2012年 ]。与基于超平面的哈希函数相比，球面哈希[ Heo等。 2012年 ]将空间相干的数据点映射成二进制代码。各向同性Hashing ( IsoHash ) [ 孔颖和李明博 2012 ]学习能够产生具有各向同性方差(等方差)的投影维数的投影函数。

曼哈顿哈希( MH ) [ 孔等人 2012年 ]在基于Hamming距离的哈希中使用曼哈顿距离处理原始特征中邻域结构的破坏。可预测的双视图哈希( PDH ) [ Rastegari等人。2013年]在原始空间中嵌入数据样本的邻近性，归纳流形哈希( IMH ) [ Shen等人。 2013年 ]连接流形学习方法和哈希函数学习。最近，Irie等人 提出局部线性哈希( LLH )，以在低维汉明空间中保留高维数据的局部线性流形结构。Zhang等人提出了另一种最新的无监督哈希方法——拓扑保持哈希( TPH )。用于保持邻域关系和相对邻域近似。

非线性无监督哈希。非线性无监督哈希不使用线性哈希函数，而是使用非线性函数，通常是一些核函数，用于无监督哈希。Kulis和Grauman 将LSH的可达性扩展到通用核空间，提出了核化LSH ( KLSH )。KLSH的主要思想是基于中心极限定理在核空间中构造随机超平面哈希函数。根据中心极限定理，在非常温和的条件下，随着集合中数据对象数量的增加，来自某种底层分布的一组数据对象的均值将在极限中很大程度上服从高斯分布。遵循这一中心极限定理，将利用数据库中的数据项计算一个近似的随机向量。在构造随机超平面哈希函数后，KLSH通过 Charikar 的方法计算出一组近似最近邻的候选集。之后，KLSH通过内核函数对它们进行排序，生成哈希最近邻居列表。因此，可以利用标准LSH技术在次线性时间内检索查询的最近邻。图8展示了内核化LSH的主要思想。

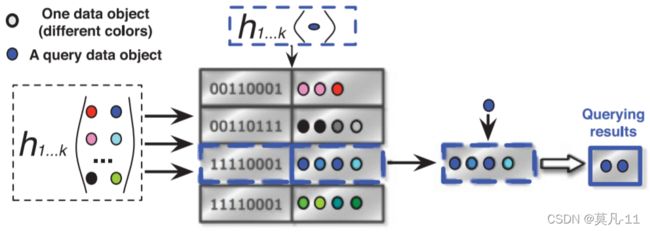图8核化LSH的核心思想是：h (*)表示一个哈希函数；数字代码表示数据对象的哈希值。

图8中，蓝点表示查询数据对象。哈希函数1…k用于将数据对象映射到一组紧凑的代码中。对于同一个紧凑代码，可能有多个数据对象倾向于彼此相似。对于紧凑代码11110001，有四个数据对象。通过将查询数据点映射到相同的紧凑代码，将搜索范围缩小到一个小范围。因此，可以很容易地找到代码11110001所代表的蓝色对象。

KLSH的一个显著优点是不存在关于输入和数据分布的假设。因此，它使得KLSH非常适合于图像搜索和其他底层数据分布未知的领域。

实际上，当代码位数较小时，KLSH的性能会恶化。他等人受大规模问题的实际需求的启发。文献提出了一种通用哈希算法，可以对任意核函数的通用数据类型进行工作。该方法具有生成高效紧凑的代码、快速的索引和搜索速度、保存多样类型的相似度( 特征相似度和语义相似度如标签一致性 )等关键优点。

大多数最新的哈希方法只使用单一的特征类型，而对于许多领域，例如图像检索，多个特征的组合被证明对学习非常有用。据此，Liu等人。[ 2012a ]提出了一种多特征核哈希( MFKH )方法，该方法兼容一般数据类型和不同视觉特征表示的不同相似性。

由于无监督哈希方法不需要任何标记数据，在给定的距离度量下，这些方法的参数通常很容易学习。但是，对于某些领域，特别是与视觉相关的问题，数据点之间的相似度(或距离)可能不容易用简单的度量来定义。同时，从一个数据集(或一个领域)中学习到的度量相似度对于另一个数据集可能并不能很好地保持语义相似度。在这种情况下，包含弱标记数据的标签信息(如两两实例标签)对于散列很有用。

4.2.2 Semisupervised Hashing

在半监督哈希中，标记数据和未标记数据都被用来训练哈希模型。代表性的方法有半监督Hashing ( SSH ) [ Wang等人。 2010a , 2012 ]、LAbel-正则化的最大边缘划分[ Mu等 . 2010年 ]、半监督判别Hashing [ Kim和 Choi 2011 ]、半监督非线性Hashing的Bootstrap序列投影学习[ Wu等。2013年]，以及半监督拓扑保持Hashing [ 张某等人。 2014a ]。在这些哈希方法中，SSH是最流行的方法之一。

表III将半监督哈希分为线性哈希和非线性哈希，这取决于哈希中使用的是线性函数还是非线性函数。

Table III. Categorization of Semisupervised Hashing Methods

Semisupervised Hashing	Linear Semisupervised Hashing
		Semisupervised Hashing (SSH)
		Semisupervised Discriminant Hashing (SSDH)
		Semisupervised Topology-Preserving Hashing (STPH)
	Nonlinear Semisupervised Hashing	LAbel-regularized Max-margin Partition (LAMP)
		Bootstrap-NSPLH

Linear Semisupervised Hashing。由于数码相机和其他成像设备的易得性，大规模图像数据集正变得迅速可用，因此迫切需要从大数据存储库进行图像搜索。不幸的是，从大型数据库中快速准确地检索图像仍然是一个重大挑战。一方面，无监督哈希方法不能有效地捕获图像搜索中的语义相似度，因为没有提供标记数据来帮助哈希函数学习语义相似度。虽然监督哈希方法可以利用标记信息来学习语义相似度，但当标记数据数量很少或标记有噪声时，它们往往会过拟合。另一方面，监督方法的训练效率相当低。受这些问题的启发，SSH方法被提出来同时处理标记和未标记数据上的度量和语义相似度。

Wang等人为了处理大规模的图像搜索，解决度量中的无监督哈希约束和监督哈希训练效率低的问题。Wang等人[ 2010a , 2012 ]提出了利用简单线性映射来处理数据中度量和语义相似度和相异度的SSH方法。这些SSH方法主要用于大规模图像搜索。

SSH的目的是将n个数据点$X=[x1,x2,...,]\in R^D$映射到一个Hamming空间，并寻求由$y\in {\left\{1,-1\right\}}^{n\ast K}$给出的X的K位Hamming嵌入。给定向量$w_k\in R^D$和$W=[w_1,...,w_k,...,w_K]\in R^{D\ast K}$，定义第$k^{th}$个哈希函数为
$${\hslash }_k(x_i)=sign(w_k^T{x}_i)$$
为了容纳数据标签，SSH允许两类标签信息。假设$\mathcal{M}$表示邻居对，C表示非邻居对，$H=[h_1,\dots ,h_k,\dots ,h_K]$是K个哈希函数的序列。SSH定义目标函数$J(\ast )$来衡量标记数据上对H的经验精度：
$$J(H)=\sum _k\left\{\sum _{\left(x_i,x_j\right)\in \mathcal{M}}{\hslash }_k\left(x_i\right){\hslash }_k\left(x_j\right)-\sum _{\left(x_i,x_j\right)\in \mathrm{C}}{\hslash }_k\left(x_i\right){\hslash }_k\left(x_j\right)\right\}$$
然后，SSH定义了一个矩阵$\mathbf{S}\in {\mathrm{R}}^{L\ast L}$，以包含成对标记信息$X_l$并表示$J(H)$：
$${\mathbf{S}}_{i,j}=\{\begin{array}{rl}1& :\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)\in \mathcal{M}\\ -1& :\left(x_i,x_j\right)\in \mathrm{C}\\ 0& :\text{ otherwise }\end{array}$$
假设$H\left(X_l\right)\in {\mathrm{R}}^{K\ast L}$将$X_l$中的数据点映射到$K$位码；SSH表示$J(H)$为
$$J(H)=\frac{1}{2}\mathrm{tr}\left\{H\left(X_l\right)\mathbf{S}H{\left(X_l\right)}^T\right\}\Rightarrow J(W)=\frac{1}{2}\mathrm{tr}\left\{\mathrm{sign}\left(W^T{X}_l\right)\mathbf{S}\mathrm{sign}{\left(W^T{X}_l\right)}^T\right\}$$
SSH的目的是学习对$\left(x_i,x_j\right)\in \mathcal{M}$赋予相同比特的最优投影W 和$\left(x_i,x_j\right)\in \mathrm{C}$的不同位：
$$\arg \underset{W}{\max }\frac{1}{2}\mathrm{tr}\left(W^{T}MW\right)$$
其中$M=X_l\mathbf{S}{X}_l^T+\eta X{X}^T,X_l\mathbf{S}{X}_l^T$表示有监督项，$\eta X{X}^T$表示无监督项( $\eta$为正标量，相对于基于方差的正则项加权)。M是调整后的协方差矩阵。在M中，有监督项旨在极大地减小对标记数据的经验误差，无监督项则试图最大化个体比特的方差和独立性，从而提供有效的正则化。此外，通过放松正交约束，在不增加计算开销的情况下，利用正交解和非正交解生成更好的哈希码。

给定一个有几个成对标记数据点的大规模未标记数据集，SSH的最终目的是学习存储紧凑、检索速度快的数据依赖哈希函数，以及更好地划分数据点。图9 ( a )展示了划分好与坏的区别，其中较好的划分允许相似对位于同一边，不同的对位于不同边。

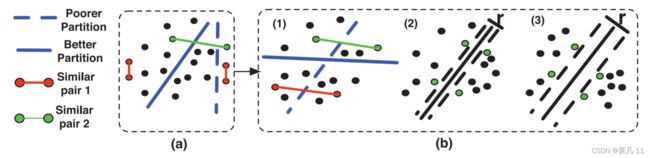图9 ( a )好分区与坏分区的比较：每个数据点代表一个实例。( b )弱监督LAbel-正则化最大边际划分( LAMP )算法的主要思想：每个点代表一个数据项。( 2 )和( 3 )中的黑点线表示数据字段的划分，γ表示划分界限。

虽然SSH是高效的，并且实现了一个非常简单的基于特征分解的解决方案，但在从一组训练数据中学习一个紧凑的二进制代码时，并没有考虑短二进制代码之间的可分性。为了解决这个问题，Kim和Choi 在线性判别分析的基础上学习了基于半监督哈希的判别二进制码，提出了半监督判别哈希( SSDH )。SSDH使用标记数据，以最大化不同类中二进制码之间的可分性，同时使用未标记数据进行正则化。实验和验证表明，对于短二进制码，SSDH确实优于SSH。

对于上述方法，哈希函数是在不考虑排序信息的情况下学习的，因此它们的哈希代码本质上忽略了排序信息，这对于相似性搜索，特别是对于$k$近邻$kNN$搜索非常重要。而且，一些保持距离的哈希方法不能很好地保存数据拓扑。据此，Zhang等人。[ 2014a ]提出了一种结合邻域排序信息和哈希函数学习的半监督拓扑保持哈希( STPH )方法来解决上述两个问题。此外，STPH还在训练数据中利用语义标签，因此其哈希结果可以准确搜索语义邻居。

Nonlinear Semisupervised Hashing。对于线性半监督哈希，现有的方法主要依赖于线性特征表示。实际上，基于内核的特征表示可能更有效地度量数据项之间的相似性，特别是对于视觉对象。据此，Mu et al . 在核空间中提出了弱监督LAbel正则化最大间隔分割( LAMP )算法，以支持基于核的特征表示。LAMP是专门为内核空间设计的，可以生成具有内核技巧和弱监督的高质量哈希函数。LAMP中的随机抽样策略使得该方法对大规模数据集具有可扩展性。LAMP的主要动机和思想如图9 ( b )所示。

在图9 ( b )中，( 1 )说明了更合理的边信息来指导哈希方案，( 2 )和( 3 )显示了两个不同的哈希函数，导致在同一分布上有不同的裕度$\gamma$(统计学术语,指留有一定余地的程度,允许有一定的误差)。图9 ( b )显示，( 1 )边信息或标签信息可以为更合理的哈希结果提供有用的指导；( 2 )较大的裕度$\gamma$可能意味着相似度搜索的错误率较低，并可导致更好的泛化能力；( 3 )对于视觉应用，如果采用基于核的特征表示，则更自然、更有用地度量相似度。与KLSH类似，LAMP也可以应用于任何图像数据库，因为它不假定输入数据中的数据分布。

另一种非线性半监督哈希算法是Bootstrap投影半监督哈希算法。对于SSH，一个限制是由于线性投影伴随均值阈值化，数据点之间的底层关系可能得不到有效反映。同时，对于高维数据点，SSH往往需要较高的计算成本。针对这一局限性，利用Bootstrap序列投影学习，提出了一种半监督非线性Hashing ( Bootstrap-NSPLH ) [ Wu等人。 2013年 ]。在Bootstrap-NSPLH中，使用一个非线性哈希函数来反映可用于半监督哈希的数据点之间的底层链接。此外，Bootstrap-NSPLH可以通过综合考虑先前学习的比特来纠正哈希过程中积累的错误。在Bootstrap - NSPLH中，与线性哈希函数相比，计算矩阵的维数要小得多，且与原始数据空间的维数无关。

4.2.3 Supervised Hashing

在有监督哈希中，有标记的数据，如每幅图像的标签或指定相似/不相似数据项对的成对约束，可用来帮助学习哈希模型。监督哈希的目标是利用基于标签的相似度或语义相似度，在数据的特征值之外，训练有效的哈希函数。

有代表性的监督哈希方法包括Boosting SimilaritySensitive Coding[ Shakhnarovich等 . 2003年 ]、Boltzmann machine-based hashing[ Salakhutdinov和 Hinton 2007 ]、Binary Reconstructive Embedding[ Kulis和 Darrell 2009 ]、Minimal Loss Hashing[ Norouzi和 Blei 2011 ]、 Kernel-based Supervised Hashing[ Liu等人。 2012b ]和Linear Discriminant Analysis-based Hashing[ Strecha等人]。2012 ]。最近，一些新的监督方法被提出，包括Similarity-Preserving Hashing[ 2012年出版商和贝尔 ]、Two-Step Hashing[ Lin等人 2013年 ]、 Multimodal Similarity-Preserving Hashing [ Masci等人 2014 ]、Semantic Correlation Maximization[ 张志刚、李明博 2014 ]、Latent Factor Hashing [ 张某等人。 2014b ]和FastHash [ Lin等人 2014 ]。

根据每种方法使用的哈希函数的实际形式，我们还将监督哈希分为线性哈希和非线性哈希。类别及相应的重要哈希算法列于表IV。

Table IV. Summary of Supervised Hashing Methods

Supervised Hashing	Linear Supervised Hashing
		Supervised Hashing with Binary Reduction
		Boosting Similarity-Sensitive Coding (BoostSSC)
		Binary Reconstructive Embedding (BRE)
		Minimal Loss Hashing (MLH)
		Latent Factor Hashing (LFH)
		Linear Discriminant Analysis-Based Hashing (LDAHash)
	Nonlinear Supervised Hashing	Kernel-Based Supervised Hashing (KSH)
		Two-Step Hashing (TSH)
		FastHash

线性监督Hashing。为了节省数据存储空间，在哈希处理中常采用二进制缩减技术。图10 ( a )显示了二元约简。

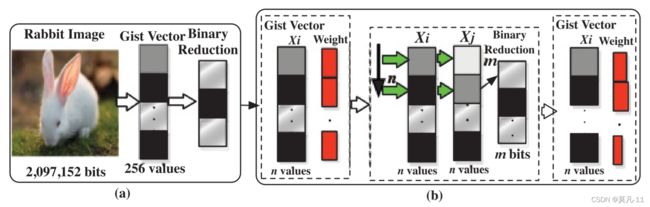图10。( a )带二进制还原的监督哈希：3种颜色的‘黑色’、‘白色’、‘灰色’分别表示主旨向量和二进制还原中的不同值。( b ) BoostSSC过程：主旨向量中3种颜色(黑色、白色、灰色)代表不同的值；红色的宽度表示主旨向量对应的权重值。

图10 ( a )显示使用二进制还原会导致显著的存储减少。在图中，主旨被定义为场景的抽象表示，它自发激活场景类别的记忆表示。原始图像有2,097,152位。通过使用主旨向量，将图像转换为256个值的主旨向量(即仅用16位表示)。

作为一种增强方法，标记图像( 正负图像对 )被用来训练二值约简的发现。为了从标记数据中学习一系列加权哈希函数，Shakhnarovich等人提出了一种新方法。提出了一种Boosting Similarity-Sensitive Coding (BoostSSC)，该技术使用加权汉明距离计算图像之间的距离，并学习原始输入空间嵌入到新空间的方法，如图10 ( b )所示。在BoostSSC开始阶段，图像主旨向量中的每个值( 图 10 ( b )中的红细胞 )的权重是一致的。对于二进制约简中的每个比特(哈希函数$H(X)$ )，BoostSSC选择在整个训练集中引起加权误差最小的索引，然后更新权值进行下一次计算。最后，二值约简中每个比特都有相应的索引和权值阈值( 在图 10 ( b )中的远右虚线框中 )。

深度神经网络也被用来从高维输入中学习紧凑的二进制代码，使用堆叠受限玻尔兹曼机器( RBMs ) [ Salakhutdinov和 Hinton 2007 ]。为了在映射到汉明空间后显式保留输入距离，Kulis和达雷尔 通过最小化输入距离与重构汉明距离之间误差的平方损失，开发了一种高效的坐标下降算法——二进制重构嵌入( Binary Retective Embedding，BRE )。BRE是一种有监督的哈希函数学习算法，用于快速准确的最近邻搜索。

在BRE中，与数据相关的比特相关哈希定义如下：
$$d_{\mathcal{M}}\left(x_i,x_j\right)=\frac{1}{2}{\Vert x_i-x_j\Vert }^2;d_{\mathcal{R}}\left(x_i,x_j\right)=\frac{1}{K}\sum _{k=1}^K{\left({\hslash }_k\left(x_i\right)-{\hslash }_k\left(x_j\right)\right)}^2$$
目标是通过最小化下面的重构误差得到最优的W：
$${\mathbf{W}}^{\ast }=\arg \underset{\mathbf{W}}{\min }\sum _{(i,j)\in \mathcal{N}}{\left[d_{\mathcal{M}}\left(x_i,x_j\right)-d_{\mathcal{R}}\left(x_i,x_j\right)\right]}^2,$$
其中，样本对集合$\mathcal{N}$表示可以根据应用程序选择的训练数据。由于符号( . )的不可微性，很难对前一目标函数进行优化。因此，BRE通过应用坐标下降算法迭代地将哈希函数更新到局部最优。

通过为每个同标号对设置一个零距离，以及为每个不同标号对设置一个足够大的距离，将BRE扩展到一个有监督的场景更加容易。

对于大规模数据集，BRE的训练效率很低，而且由于昂贵的存储开销，BRE在大规模数据集上的训练几乎是不现实的。为了解决这一局限性，Norouzi和Blei 在一类通用的损失函数下，提出了基于潜在结构SVM框架的最小损失Hashing ( Minimal loss Hashing，MLH )，适用于使用欧氏距离进行训练或使用一组标记数据点。为了进一步提高训练效率，Zhang等人提出了潜在因子Hashing ( LFH )学习保持相似度的二进制码。为了在大规模数据集上训练LFH，作者采用随机线性时变学习方法。同时，对于大规模数据集，存在检索和匹配问题。为了存储和检索描述符数据，Strecha等人 提出了基于线性判别分析的Hashing ( LDAHash )，将描述符向量映射到汉明空间，并通过将其表示为短二进制串来减小描述符的大小。

非线性监督Hashing。典型的非线性监督哈希方法包括基于核的监督哈希( KSH ) [ Liu等人。 2012b ]、两步哈希( TSH ) [ Lin等人 2013年 ]和FastHash [ Lin等人 2014 ]。其中，KSH和TSH都使用核函数作为非线性哈希函数，FastHash使用增强决策树实现哈希的非线性。

目前，哈希方法主要用于解决大规模数据问题。通过将监督信息杠杆化到哈希函数学习中，可以提高哈希质量。为了进一步提高哈希性能，解决冗长模型的训练问题，Liu等人提出了一种新的算法。[ 2012b ]提出了一个KSH模型。该模型在将数据映射到紧致二进制码时，最小化相似数据对之间的汉明距离，最大化不同数据对之间的汉明距离。在优化码内积和调整汉明距离的同时，利用等价性对哈希函数进行一次 1bit 的顺序训练，以获得短且具有区分性的码。图11演示了KSH的主要过程。

图11. 监督核哈希 ( KSH )的核心过程：不同颜色的圆代表不同的数据。‘哈希码矩阵’中的绿色网格表示哈希码中的调整部分。

在图11中，标记数据有相似对和不同对。每个数据点都有相应的哈希码。KSH首先通过最小化相似对之间的汉明距离和最大化异对之间的汉明距离来优化汉明距离(见"汉明距离优化"的点列框)，然后将这些哈希码合并为一个矩阵。通过使用矩阵乘法( 见命名为‘代码内产品优化’的虚线框。 )，KSH通过命名为“哈希码矩阵”的虚框中的最终哈希码矩阵进一步调整汉明距离。

实际中，KSH的优化过程耦合到指定的哈希函数中，限制了优化的应用范围。考虑到容纳不同的损失函数和哈希函数，一种新的两步哈希( TSH ) [ Lin等人 2013年 ]提出了一个灵活而简单的框架，该框架基于哈希函数学习过程和代码生成可以看作是分离的步骤，而前者可以通过训练标准的二进制分类器来实现。因此，哈希学习分为两个阶段：哈希比特学习和利用学习到的比特进行哈希函数学习。

两步哈希方法也被应用于具有高维特征的大规模数据集，其中核哈希函数的训练和测试代价非常昂贵。为了解决这个问题，FastHash [ Lin等人 2014 ]首先使用决策树作为非线性哈希函数处理大规模高维训练和测试数据。进一步应用了两步学习策略，将二进制代码推理和简单的二进制分类训练相结合，形成学习过程。

由于具有强大的泛化能力，非线性哈希函数在整体性能上通常优于线性哈希函数。

总之，与无监督哈希方法相比，有监督哈希方法的主要优点是对不同的实际应用具有灵活性和适应性。然而，培训效率仍然是一个很大的挑战。

4.3 Cryptographically Secure Hashing

对于加密安全哈希(或密码学哈希)，哈希函数不仅将任意长度的输入压缩为固定长度的输出，而且设计为单向，具有三个主要性质：原像抵抗、第二原像抵抗和碰撞抵抗。这些属性可以保证( 1 )输入数据很难由给定的哈希值生成，( 2 )很难找到具有相同哈希值的两个不同输入。

随着身份验证和数字验证在数字签名、公钥密码等应用中的日益普及，密码学哈希技术最近得到了显著的关注。例如，在数字签名中，加密哈希可以用来为一个消息生成摘要，而加密的摘要，使用一个秘密密钥，可以看作该消息的数字签名。

根据哈希函数是否使用密钥，加密哈希可分为两类：未插入密钥装置的加密哈希和密钥加密哈希。

Table V. Summary of Cryptographic Hashing Methods

Cryptographic Hashing	Keyed Cryptographic Hashing
		VMAC; UMAC; PMAC; OMAC; HMAC
		Poly1305-AES; MD6; BLAKE2
	Unkeyed Cryptographic Hashing	MD2/4/5/6
		SHA-1/3/224/256/384/512
		HAVAL; GOST; FSB; JH; ECOH
		RIPEMD/-128/-160/-320

4.3.1 Unkeyed Cryptographic Hashing

未插入密钥装置的密码哈希是指在哈希过程中不需要安全密钥来证明哈希安全性的方法，而哈希函数是专门为哈希设计的。虽然未插入密钥装置的加密散列中没有涉及密钥，但它仍然满足一般加密散列所要求的基本安全策略。

存在许多未插入密钥装置的加密哈希方法。其中，MD5和SHA在应用中比较流行。接下来，我们简要介绍了MD家族的发展历史，并对其他相关方法进行了综述。

‘MD’( "Message Digest"的缩写 )表示RSA数据安全公司R . Rivest设计的一系列哈希函数。在MD-家族中，MD1是一种专有的方法，MD2旨在为任意长度的消息生成一个简单的16字节消息摘要，具有两个声称性质：( 1 )给定一个消息摘要，查找消息的难度按照2128次操作的顺序进行；( 2 )给定相同的消息摘要，查找两个不同消息的难度按照264次操作的顺序进行。然而，有几部著作揭示了MD2的一些弱点，如来自MD2的哈希函数的碰撞[ Rogier和Chauvaud 1997 ]。因此，2004年，MD2被定义为一个不安全的单向哈希函数。MD4 [ Rivest 1992 ]是由Ronald Rivest于1992年提出的，长度为128字节的摘要消息。对于发现碰撞困难的说法与MD2’s相同，但Den Boer和Bosselaers 发现了对最后两轮MD4的攻击。为了加强MD4，建议MD5 [ Rivest 1992 ]增加一轮。尽管MD5是最有前途的哈希方法之一，而且对完整的MD5还没有任何成功的攻击，但是当前的大数据环境需要一个更快的哈希方法。MD6 [ Rivest等。 2008年 ]是为了更好地满足哈希需求而提出的，其中消息摘要的长度可以灵活地从1位设置为512位。MD6具有良好的效率，可以支持多个处理器。

另一个重要的未插入密钥装置的密码学哈希是SHA [ FIPS1995 ]，它是MD4的更新版本，有两个主要区别：( 1 )消息摘要的长度为160字节，( 2 )每轮的步数为20步，比MD4的16步长。HAVAL [ 郑等人.1992年 ]也是一种流行的未插入密钥装置的密码学哈希，类似于MD5，但由于哈希长度可以包含多个字节选项( 128或256 )，且轮数可以由用户指定，因此更加灵活。

许多其他未插入密钥装置的密码学哈希函数，如BLAKE家族、RIPEMD家族、ECOH [ Brown等 . 2008年 ]、FSB家族[ 俄戈特等人 2005年 ]和GOST [ Mendel等人.2008 ]，也存在面向安全的应用。

4.3.2 Keyed Cryptographic Hashing

虽然未插入密钥装置的密码学哈希(如MD5或SHA )是非常流行的，但是它并不安全。在密钥加密哈希中，使用一个密钥来增强安全性，如图12所示。为了保护信息的真实性，通常采用消息认证码( MAC )的形式，通过哈希机制计算出一个名为认证标签的值，该值可以作为密钥并附加到消息中。如果不知道这个秘密密钥，即使哈希函数已知，也很难检索到消息。密钥往往在双方之间共享，因此这种密码方案只能避免局外人攻击。许多应用程序，如消息身份验证、密码检查和加密，都需要密钥加密哈希的技术保证。

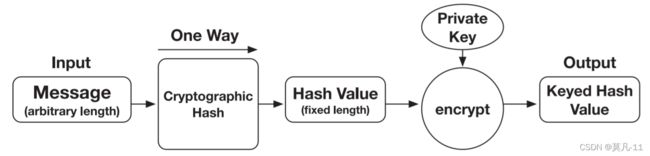图12 .密钥加密哈希方案：单向加密哈希函数处理任意长度的输入消息，产生一个固定长度的哈希值，将其与私钥结合，产生密钥哈希值。

有不同类型的MAC，如基于通用哈希的消息认证码( UMAC )、基于块密码子的消息认证码算法( VMAC )、单密钥MAC ( OMAC )、可并行MAC ( PMAC )和带密钥哈希的消息认证码( HMAC )。所有这些MAC都享有可证明的密码强度。其中，UMAC和VMAC均基于通用哈希，UMAC为32位体系结构设计，VMAC同时支持32位和64位体系结构。与其他MAC相比，UMAC具有更高的计算效率。VMAC是专门针对64位CPU结构而设计的，它可以获得非常优异的性能。PMAC使用分组密码创建一个高效的消息认证码，在安全性上可证明可还原为基础分组密码。OMAC在功能上与PMAC类似，其消息认证码由分组密码构造。HMAC是一种特殊类型的MAC，它不仅考虑了密码学密钥，还考虑了密码学哈希函数。而且，与任何MAC一样，HMAC可以同时验证数据完整性和消息的认证性。而且任何加密哈希函数都可能参与一个HMAC的计算。许多元素可以用来确定HMAC的密码学强度，如输出大小、底层哈希函数以及密钥的大小和质量。

我们前面的描述主要集中在MAC-家族哈希方法。另外一些密钥加密哈希函数，如Poly1305 - AES [ Bernstein 2005 ]、SipHash [ 2012年奥马森和伯恩斯坦 ]和BLAKE2 [ Aumasson等人 2013年 ]等，也存在，但由于页面限制，无法进行详细的处理。

---

4.4 Cryptographically Insecure Hashing

密码不安全哈希也称为非密码哈希，与密码哈希有一个相似的目标，即以可变大小的消息作为输入，返回一个小于输入消息的恒定大小的哈希值。然而，哈希过程不需要考虑密码学，其基本目标是尽可能地减少碰撞，提高哈希速度。对于这种哈希函数，不需要哈希运算的秘密信息，并且公开了哈希函数的描述。

例如，在安全和法医分析中，发现和发现相似或同源的物体是常见的。虽然加密散列通常提供一个是/否或$1/0$的答案来比较和查找相同的对象，但不能直接和有效地应用于需要一系列结果的应用程序$[0,1]$，其结果被解释为相似性度量。因此，可以使用密码学上不安全的哈希技术，如近似匹配，为查找相似或相同的对象提供近似匹配值( 相似性度量 )。在提出近似匹配方法之前，针对不同的应用有几种相关的方法。前一种是上下文触发分段哈希( Context- Triggered Piecewise Hashing，CTPH )，它通过在文件之间建立关联来识别同源文件(不完全相同的文件)，帮助调查者快速找到相关文件或材料。CTPH将密码学哈希的传统用法推广到计算机取证。对于数据指纹，Roussev 提出了一种具有相似摘要的相似思想来生成数据指纹。所有这些近似匹配方法都更适应于一般的安全和取证分析。在图像识别应用中，由于当前哈希方法对图像处理操作的脆弱性，为了支持快速稳定的图像处理，利用密码哈希和图像识别方法的优点，提出了一种高效的鲁棒图像哈希方法（Steinebach等人）。

与加密哈希相比，非加密哈希没有哈希操作的秘密信息。该类方法具有四个重要特点：( 1 )哈希速度快；( 2 )碰撞概率低；( 3 )错误检测概率高；( 4 )易于碰撞检测。因此，它们被广泛地应用于输入数据量大、需要快速搜索或处理的应用中，例如在Twitter情感分析中使用MurmurHash3哈希( 非加密哈希函数 )进行特征哈希[ Silva等人 2014 ]。

对于几乎所有的非加密哈希函数，基本方案是相同的，如图13所示，称为Merkle-Damgard结构，其中输入消息被分成多个块，每个块都由相应的混合函数处理。最后，将所有处理的碎片合并在一起，生成哈希输出。

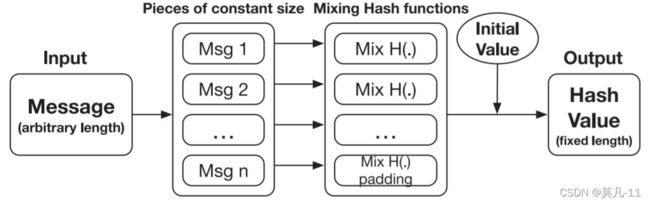图13. 一般的非密码学哈希方案：一个输入消息被分成多个长度固定的片断，每个片断被一个混合哈希函数处理。将初始值与每一块的哈希值结合，生成一个固定大小的哈希值。

Table VI. Noncryptographic Hashing Categorization

Noncryptographic Hashing	FNV Hash; xxHash; SuperFastHash
	MurmurHash2; lookup3; Pearson Hashing; BuzHash
	Approximate Matching
	DEK; BKDR; APartow; DJBX33A

许多非密码学哈希函数已经被提出，在本次调查中我们重点关注最常见的哈希函数。Fowler-Noll-Vo ( FNV )哈希函数是针对快速哈希表和 校验和 而提出的一种早期的非加密哈希方法。FNV最明显的优点是实现简单。另一个值得一提的是 Lookup3，它主要产生32位的哈希表查找。Lookup3是非密码学哈希方法中最重要的一种，已经在很多产品中得到应用，如Oracle和Google。受FNV和Lookup3的思想启发，SuperFastHash [ Hsieh 2004 ]被提出，以实现极高的速度，并为软件产业提供雪崩效应。对于开源项目，另一种哈希方法MurmurHash2 [Appleby 2008 ]由于其非凡的雪崩特性，在短时间内非常流行。对于哈希字符串，DJBX33A被设计并广泛应用于许多编程语言和应用服务器中，如Python、PHP5和Tomcat。对于一般用途，BuzHash是1992年由RobertUzgalis设计的。在BuzHash中，一个替换表用来用一个随机别名替换每个输入片，这个设计可以适用几乎所有的输入分布。此外，在"通用哈希函数库"(“General Hash Function Library”) [ Partow 2013 ]中，有三种流行的非加密哈希函数：DEK [ Knuth 1998 ]、BKDR [ Ritchie等人 1988年 ]和APartow [ Partow 2013 ]。在这三者中，乘法哈希DEK被认为是最早也是最简单的哈希方法之一，现在仍然流行。最近，一种新的哈希函数$xxHas{h}^2$以其极快的处理速度，在$RAM$限制下运行，受到了广泛的关注。xxHash 可以支持32位和64位，在数据库和游戏行业得到了广泛的应用。

对于非密码学哈希，其质量标准包括抗碰撞、输出分布、雪崩效应和速度。对于抗碰撞，非密码学哈希试图减少碰撞，但由于它们不遵循密码学哈希使用的三个安全属性，因此碰撞仍然是可观察的。对于输出的分布，非加密哈希保持哈希输出均匀分布是非常重要的，因为分布的不均匀可能导致聚类问题，影响哈希函数的性能。对于雪崩效应，如果能够观察到输入发生非常微小的变化，那么输出发生很大变化将非常有助于避免聚类问题。对于速度，非加密哈希应尽可能快地执行，以提高哈希效率。根据Estebanez等人的实验分析，MurmurHash2、SuperFastHash和 Lookup3雪崩效果最好，Lookup3、MurmurHash2和SuperFastHash更适合通用。

---

4.5 计算复杂度

我们从哈希方法的计算效率和内存消耗两方面简要回顾了哈希方法的计算复杂度。在我们的分析中，我们定义了一个汉明空间为所有长度为$N$的$2^N$个二进制串的集合。

简单来说，数据相关哈希通常使用训练数据来学习所有数据记录具有最佳紧凑代码的哈希函数。因此，它可以实现比数据无关哈希快得多的查询时间和更少的内存消耗。但是，由于数据依赖哈希需要额外的训练时间，因此不能任意确定整体的时间性能差异。面向安全的哈希主要是更关注安全属性，比面向数据的哈希码具有更长的哈希码。因此，面向安全的哈希方法往往比面向数据的哈希方法更昂贵，效率也更低。与密码学安全哈希相比，密码学不安全哈希无需考虑密码学，只需要减少碰撞，从而尽可能提高哈希速度。因此，加密不安全哈希通常比加密安全哈希更有效。

在表七和表八中，我们总结了不同类别方法的运行时复杂度和空间消耗。

( 1 )对于data-independent hashing，random projection hashing是一种计算效率高的方法，它将高维(d)数据随机投影到较低维(b)子空间中。对于n个输入项，空间消耗为$d\times lgb$比特，时间复杂度为线性$O(dbn)$。一种改进的哈希方法——universal hashing，从一个特定的函数集合(而不是所有函数)中随机选择一些哈希函数，因此其空间复杂度为$n\times lgd$，时间复杂度为$O(n)$。对于另一种常见的哈希LSH，假设哈希表大小为$k$，函数宽度参数为$w$，空间为$O(nk)$，处理时间复杂度为$O(nkw)$。下一个值得一提的哈希方法是MinHash，它需要$O(nk)$时间和每个单置换的$O(n)$位。总之，大多数数据无关的哈希方法需要线性时间复杂度。

( 2 )对于数据依赖的哈希，其时间复杂度可以分为两部分：( 1 )训练复杂度和( 2 )码字计算复杂度。对于谱哈希，其训练时间为$O(n^3)$，码字计算时间为$O(rn)$，其中r为汉明空间的维数。相比之下，AGH，一种流行的线性无监督哈希方法，可以在$O(n)$时间内构建一个结果图。另一种类似的哈希方法LLH使用m大小的子集作为样本训练数据。训练时间复杂度为$O(m^2)$，编码时间复杂度为$O(m)$，空间复杂度为$O(m)$。对于非线性无监督哈希( KLSH )，构造矩阵的训练时间复杂度为$O(p^3)$，每个哈希函数的编码计算复杂度为$O(p^2)$，其中p为数据库对象的样本容量。当$p=O(\sqrt{n})$时，KLSH逼近次线性搜索时间。SSH放松了PCA的正交性约束，实验证明它与LSH具有相同的运行时间。对于有监督哈希，每次迭代都需要更新哈希函数，BRE的时间复杂度为$O(nb(k+logn))$ (其中k表示每个输入数据的最近邻个数，b表示一个哈希表的比特大小)。总而言之，虽然一些数据相关哈希具有线性时间复杂度，但少数方法确实需要多项式时间复杂度。

( 3 )加密安全哈希必须满足原像抵抗、第二个原像抵抗和碰撞抵抗。对于大小为n的消息，哈希值的计算复杂度为$O(n)$。为了抵抗原像，必须创建$2^{n-1}$个消息，复杂度为$O(2^n)$。同时，由于第二原像是抵抗的，时间复杂度也是$O(2^n)$。对于具有抗碰撞性，由于随机性，如果攻击者希望找到两个哈希值相同的消息，则需要执行几乎$2^{n/2}$的哈希操作。因此，综上所述，加密安全哈希的总体复杂度为$O(2^n)$。

( 4 )对于加密不安全的哈希，哈希函数主要针对快速哈希表和校验和使用。理想情况下，无论数据大小如何，加密不安全哈希都有可能在恒定的时间内搜索数据$O(1)$。特别是对于一些非常快速的哈希，比如$xxHash$，速度几乎接近RAM的极限。对于其他常见的非加密哈希函数，Estebanez等人如的实验研究所示的速度很大程度上取决于哈希密钥的大小。对于长键，SuperFastHash和MurmurHash2表现最好。与加密不安全哈希类似，空间复杂度还取决于每个消息的输出大小。但不同的是，加密不安全哈希中的输出大小一般比加密安全哈希中的输出大小要短，后者强调安全属性。

---

5. Hashing方法的应用

5.1 面向数据的应用程序

从数据域的角度来看，哈希已经被广泛应用于图像、网络、图文以及数字签名等多种应用中。

由于图像数据的普及以及这些应用涉及的数据量大、维数高，大多数哈希方法都是针对图像域设计的。图像应用的主要目标是图像检索。在搜索与查询图像相关的图像时，直接比较原始特征空间中图像之间的相似度是计算代价高、耗时长的。为了实现快速的相似度计算，提出了多种哈希方法。在这些方法中，Kulis等人 用学习度量构造了用于快速近似相似搜索的 locality-sensitive hashing，并推广了以适应任意kernel fucntion，特别是图像检索任务。Wang等人 设计了一种半监督哈希方法来学习高效的哈希码来处理图像间的度量和语义相似度。另一种方法提出使用带有查询自适应重排序的Boosting iterative quantization hashing 进行大规模图像检索。Yu等人 采用无监督PCA哈希进行大规模医学图像搜索，这是医生寻找类似临床病例的独特方式。在其他图像应用中，Wang等人 设计了AnnoSearch来注释图像，Chum等人和Li等人 分别使用MinHash和Spectrum hashing进行快速图像索引。

在互联网上，哈希技术被用来解决许多挑战。例如，IP地址查找是时间敏感的，其速度很大程度上影响整个网络性能。受哈希思想的启发，Martinez等人 提出了计算机网络中IP地址查找的不同哈希方法。具体而言，Martinez等人 提出了一种优化的异或哈希，以方便线性分布的地址查找。为了进一步适应不同的分布，Martinez和Lin 提出了一种适用于所有实际数据库的自适应哈希，特别是针对非均匀分布的IP地址查找。Martinez等人文献提出了一种基于异或运算提取一定规律性的预处理方法。

对于其他与网络有关的应用程序，Lu等人 设计了一个硬件友好的最小完美哈希方案，可用于路由查找、数据包分类和监控。Choi等研究了这一问题，为了改进网络入侵检测中的数据包分类，分别采用maximum entropy hashing 和 rule hashing。

图结构数据在生物、化学、健康信息学和通信网络中普遍存在。对于所有这些应用，支持对图结构数据的高效访问至关重要。Ou等 为Facebook、Flickr和Twitter等异构网络应用了异构哈希技术。Weiss等 和Liu等人 研究了图数据库的理论哈希算法设计，分别提出了用于图划分的谱哈希和锚图哈希。同时，哈希技术也可以用来支持快速的图分类。在Li等人那里我们引入了结构化数据的NSH，并提出了一种基于DIscriminative Clique Hashing ( DICH ) [ Chi等 . 2013年 ]的快速图流分类方法。

对于文本应用程序，Chi等人和Xu等人 使用了基于 Recursive Min-wise Hashing ( RMH )和 multidimensional progressive perfect hashing 的context-preserving hashing，用于快速文本分类和字符串匹配。Jin和Yoo, Mu等人, Zhu等人 和Song 设计了不同的哈希方法，用于高效的大规模多媒体搜索，以及Yue等人 针对大规模掌纹数据库(palm-print databases) 采用了基于哈希的快速掌纹识别。

---

5.2 面向安全的应用程序

面向安全的哈希常用于与信息安全相关的应用中，如数据完整性和来源的验证、数字签名等，数据认证，消息认证码 和 加密。

( 1 )数字签名：常用于数字签名中的密钥加密哈希函数，其中签名是由消息生成的密码值和密钥，密钥只为签名者所知。对于消息接收者来说，他们只需要使用公钥进行验证，确保消息真正来自发送者，因此私钥用于消息签名，公钥只用于消息验证。在签名过程中，私钥与签名算法的哈希值(来自加密哈希)一起工作，生成数字签名，数字签名被附加到消息后发送给收件人。在验证过程中，接收者利用公钥对签名进行验证，以获得一个输出。同时，收件人可以使用发送者使用的相同哈希函数对接收数据进行哈希，以获得哈希值。通过比较这个哈希值和来自验证算法的输出，接收者可以判断数字签名是否起源于发送方。这样的数字签名框架可以扩展到数据完整性的数据认证和验证，如图像认证[ Schneider和 Chang 1996 ]。

( 2 )消息认证码：在安全应用中，伪造用户可以伪造为另一个用户发送消息，而消息认证码是用来防止这种攻击的，其中消息认证码只能由原始发送方创建。当多方需要通信时，密钥加密哈希函数可以为所有参与各方产生共享的秘密密钥进行消息认证，这将验证数据的独创性，避免局外人攻击。UMAC [ Black等 . 1999年 ]、VMAC、OMAC [ Iwata和Kurosawa 2003 ]、PMAC和HMAC [ Krawczyk等 研究了这一问题.1997年 ]都是专门为快速安全的消息认证而设计的。

---

6. 结论

在本调查中，我们将现有的哈希技术归类为具有两个主要组的层次分类，面向数据的哈希和面向安全的哈希。前者旨在通过开发高效的哈希机制加快数据访问速度，后者侧重于使用哈希生成用于验证的消息摘要(或签名)。面向数据的哈希包括两个子群：数据无关哈希和数据依赖哈希。对于与数据无关的哈希，哈希函数是独立于所要处理的数据而定义的，不涉及数据的训练过程。另一方面，与数据相关的哈希定义并学习关于给定训练数据集的哈希函数族。对于面向安全的哈希，我们将其方法分为加密安全哈希和加密不安全哈希。进一步总结了哈希方法的计算复杂度和在各组中的应用。我们的调查回顾了每一类主流哈希技术的独特性和方法，并总结了涉及哈希的主要领域应用。该综述从技术和应用角度为现实的实现提供了实践参考，也为今后的发展提供了深入研究指导。

参考文献

【1】Florida Atlantic University, Boca Raton, FL; Fudan University, Shanghai, China. Hashing Techniques: A Survey and Taxonomy