排序算法 - 时间复杂度O(N²)的冒泡、插入、选择排序
目录
1、冒泡排序
2、插入排序
3、选择排序
4、为什么很多排序工具使用插入排序而非冒泡排序?【性能】
![]()
排序是算法中比较常用的一大块,很多的场景都需要进行排序操作,而排序选择不当可能造成千、万被的性能差距。所以按照时间复杂度将排序算法进行分类,只是排序时间复杂度只是衡量数据规模趋势与耗时的关系,如果只是基于时间复杂度进行考虑那么时间复杂度高的基本就不会使用了。大O时间复杂度分析忽略了常数、系数、低阶等,然而在数据量比较小的情况下,可能常数等的值比较大,耗时完全超过了递增的趋势值,所以一个优秀的排序工具在使用时候,会考虑各种情况下都能得到比较好的性能。后面专门对Java的排序算法进行分析。针对各种排序算法的图形动态过程可以参见(整个排序过程比较直观):https://visualgo.net/zh/sorting
按照时间复杂度将排序进行分类:
O(N²)时间复杂度: 冒泡排序、插入排序、选择排序
O(N*logN)时间复杂度:归并排序、快速排序、插入排序的优化 二分插入排序和希尔排序
O(N)时间复杂度:桶排序、计数排排序、基数排序
其他排序:堆排序、猴子排序、面条排序、睡眠排序
排序不仅要考虑时间复杂度,还需要考虑空间使用率,我们将不需要额外的空间(空间复杂度为O (1) )的排序称为原地排序。三种O(N²)时间复杂度都不需要申请额外的容器,详见下面的代码,所以都是原地排序。排序时两个元素排序字段的值相等,排序之后是否还能保住原来的顺序称为稳定排序。处理是否原地排序,是否稳定排序也是非常重要的衡量指标,比如我们已经有一部分订单数据按照时间进行了排序,此时需要按照金额进行排序,如果是否非稳定排序后,则违背了我们已经按照订单时间排好序的数据。
排序时非常频繁的动作就是比对和换位,常用的换位方式有两种:使用临时变量记录其中某个值,最后再赋值回来;另一种排序方式是进行计算,前提是要计算方式不能丢失数据精度等。
// 基于计算的交换
public static void swap(int []arr, int a, int b) {
arr[a] = arr[a] + arr[b];
arr[b] = arr[a] - arr[b];
arr[a] = arr[a] - arr[b];
}
// 基于临时变量的交换
public static void swap2(int[] arr, int a, int b) {
int tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
冒泡、插入、选择排序的时间复杂度为O(N²),就是因为其排序思路比较简单都是直接采用两层for循环。排序时具体的耗时与本身的有序度相关,三种排序方式的最好时间复杂度都是O(N),需要将所有数据遍历一遍,即数据是满有序度。最坏情况就是两层for循环全部执行完,最坏时间复杂度为O(N²)。
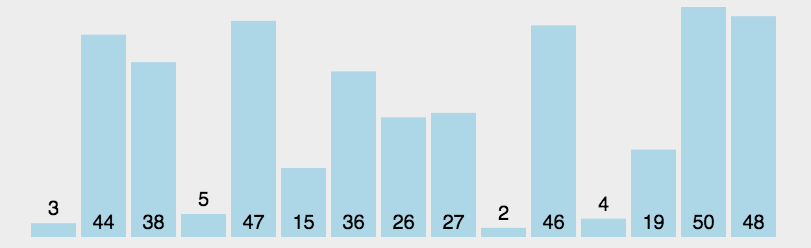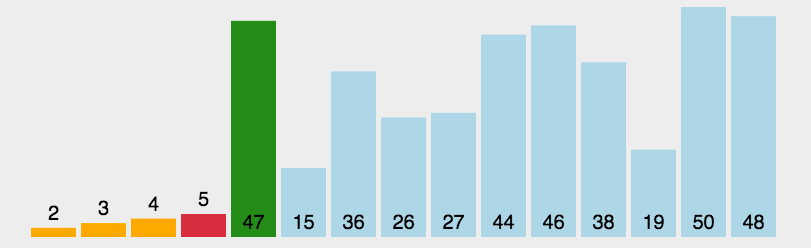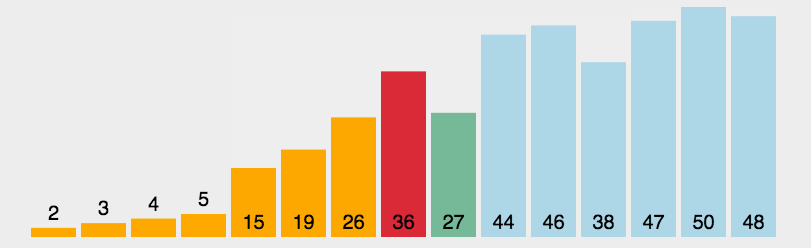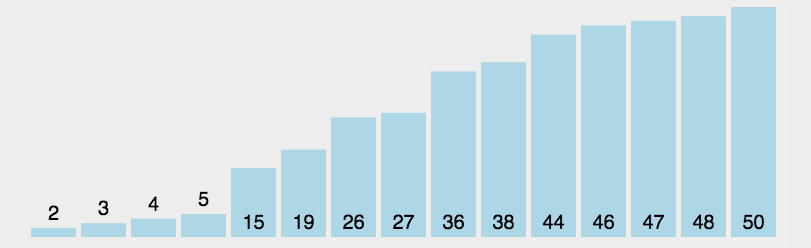
1、冒泡排序
冒泡排序思想就是将数组从头到尾,相邻两个元素挨个比对或更换,最坏更换N轮的情况下整个数组就是有序的了。冒泡排序挨个比对替换,我们可以控制相同值的不用替换,所以冒泡排序是稳定排序。
冒泡排序优化:有时候后面的部分数据本身就是有序的,那么则不需要遍历更新,则需要一个指针记录每一轮没有更新过数据的最后一位,下次排序到这里就不用继续了。
/**
* 冒泡排序
*
* 就是每次比较相邻的两个元素,如果不符合顺序则进行交换,直到某次没有交换过任何数据说明已经有序
* 最好时间复杂的是本身就有序,那么也需要便利一遍即 O(n)
* 最坏时间复杂的就是两层循环每次都跑完,那么时间复杂度就是 O(N²)
*
* @author kevin
* @date 2021/2/21 23:28
* @since 1.0.0
*/
public class BubbleSort {
public static void main(String[] args) {
int[] array = new int[]{12, 34, -34, 454, 657, 33, 89, 67, 68, 99, -23, 34};
System.out.println("排序前:" + Arrays.toString(array));
// bubbleSort(array);
bubbleDownSort(array);
System.out.println("排序后:" + Arrays.toString(array));
}
/**
* 冒泡排序
* @param array 待排序的数组
*/
public static void bubbleSort(int[] array) {
if (array.length < 2) {
return;
}
for (int i = 0; i < array.length; i++) {
boolean isChanged = false;
for (int j = 0; j < array.length - i - 1; j++) {
if (array[j] > array[j + 1]) {
isChanged = true;
int tmp = array[j];
array[j] = array[j + 1];
array[j + 1] = tmp;
}
}
// 如果上一轮没有进行任何的数据交换,则说明已经有序直接退出
if (!isChanged) {
break;
}
}
}
/**
* 冒泡排序的改进方案
*
* 每次记录最后一次进行位置交换的点,作为下次比较的边界,节省了该部分的比较操作
*
* @param array 待排序的数组
*/
public static void bubbleSortOptimization(int[] array) {
if (array.length < 2) {
return;
}
// 记录最后一次交换的点
int lastChangePoint = 0;
// 记录无序数组的边界,每次比较到该处即可,后面已经是有序的
int sortBoeder = array.length - 1;
for (int i = 0; i < array.length - 1; i++) {
boolean isChanged = false;
for (int j = 0; j < array.length - sortBoeder; j++) {
if (array[j] > array[j + 1]) {
swap(array, j, j + 1);
lastChangePoint = j;
isChanged = true;
}
}
sortBoeder = lastChangePoint;
// 如果上一轮没有进行任何的数据交换,则说明已经有序直接退出
if (!isChanged) {
break;
}
}
}
/**
* 交换数组中 两个下标位置的值
* @param array 待排序数组
* @param i 需要交换的下标 1
* @param k 需要交换的下标 2
*/
private static void swap(int[] array, int i, int k) {
int tmp = array[i];
array[i] = array[k];
array[k] = tmp;
}
/**
* 向下冒泡。可能比冒泡更易懂?
*
* 算法概要:
* 从0开始,用这个元素去跟后面的所有元素比较,如果发现这个元素大于后面的某个元素,则交换。
* 3 2 6 4 5 1
* 第一趟是从 index=0 也就是 3, 开始跟index=1及其后面的数字比较
* 3 大于 2,交换,变为 2 3 6 4 5 1,此时index=0的位置变为了2
* 接下来将用2跟index=2比较
* 2 不大于 6 不交换
* 2 不大于 4 不交换
* 2 不大于 5 不交换
* 2 大于 1,交换,变为 1 3 6 4 5 2,第一趟排序完成。
*
* 第二趟是从 index=1 也就是 3,开始跟index=2及其后面的数字比较
* 3 不大于 6 不交换
* 3 不大于 4 不交换
* 3 不大于 5 不交换
* 3 大于 2,交换,变为 1 2 6 4 5 3,第二趟排序完成。
*
* 第三趟是从 index=2 也就是 6,开始跟index=3及其后面的数字比较
* 6 大于 4,交换,变为 1 2 4 6 5 3, 此时 index = 2 的位置变为了4
* 接下来将用4跟index=4比较
* 4 不大于 5 不交换
* 4 大于 3,交换,变为 1 2 3 6 5 4,第三趟排序完成。
*
* 第四趟是从 index=3 也就是 6,开始跟index=4及其后面的数字比较
* 6 大于 5,交换,变为 1 2 3 5 6 4, 此时 index = 3 的位置变为了5
* 接下来将用5跟index=5比较
* 5 大于 4,交换,变为 1 2 3 4 6 5, 第四趟排序完成。
*
* 第五趟是从 index=4 也就是 6,开始跟index=5及其后面的数字比较
* 6 大于 5,交换,变为 1 2 3 4 5 6, 此时 index = 4 的位置变为了5
* 接下来将用5跟index=6比较
* index = 6 已经不满足 index < length 的条件,整个排序完成。
*/
private static void bubbleDownSort(int[] arr) {
int len = arr.length;
if (len == 1) {
return;
}
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++) {
if (arr[i] > arr[j]) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
}
}
}
2、插入排序
插入排序的思想就是每次轮训都让前N个元素有序,让第N个元素插入合适的位置。插入排序可以控制插入时,在相同元素值的后面,所以插入排序也是稳定排序。
插入排序本身性能比较低,但是有很多基于插入思想的优化方式,二分插入排序、希尔排序。
public static void main(String[] args) {
int[] array = new int[]{12, 34, -34, 454, 657, 33, 89, 67, 68, 99, -23, 34};
System.out.println("排序前:" + Arrays.toString(array));
insertionSort(array);
System.out.println("排序后:" + Arrays.toString(array));
}
/**
* 插入排序
* @param array 待排序的数组
*/
public static void insertionSort(int[] array) {
if (array.length < 2) {
return;
}
for (int i = 0; i < array.length; i ++) {
int value = array[i];
int j = i - 1;
for ( ; j >= 0; j--) {
if (array[j] > value) {
array[j + 1] = array[j];
} else {
break;
}
}
array[j + 1] = value;
}
}
3、选择排序
选择排序的思想就是排序好之后每个下标位置上的值是固定的,那么每次遍历获取需要处理的下标记录当前的最小值。其他每轮更小的值,已经排好序,后续不用处理。选择排序是非稳定排序。
public class SelectionSort {
public static void main(String[] args) {
int[] array = new int[]{12, 34, -34, 454, 657, 33, 89, 67, 68, 99, -23, 34};
System.out.println("排序前:" + Arrays.toString(array));
selectionSort(array);
System.out.println("排序后:" + Arrays.toString(array));
}
/**
* 选择排序,a表示数组,n表示数组大小
* @param a 待排序数组
*/
public static void selectionSort(int[] a) {
int n = a.length;
if (n <= 1) {
return;
}
for (int i = 0; i < n - 1; ++i) {
// 查找最小值
int minIndex = i;
for (int j = i + 1; j < n; ++j) {
if (a[j] < a[minIndex]) {
minIndex = j;
}
}
// 交换
int tmp = a[i];
a[i] = a[minIndex];
a[minIndex] = tmp;
}
}
}
4、为什么很多排序工具使用插入排序而非冒泡排序?
由于选择排序本身是非稳定排序,所以基本上都不会进行选择。比如上面的订单排序的例子,使用Java类库提供的排序工具,结果排序完成后得到了非期待的结果。
排序动作影响性能一个因素就是比对和交换【比对和交换动作都需要CPU进行 读取-计算-写入操作】,即其他大环境(排序思想)确定的情况下,想要将排序性能做到极致,就需要关注具体的细节。冒泡排序和插入排序虽然都是O(N²)的时间复杂度,但是由上面的代码可知,不论待排序的数组的有序度如何,冒泡排序的交换次数是固定的。插入排序的交换次数与待排序数组的逆序度相关,也是固定值。但是基于上面的代码,分析两者的比对和交换操作:
冒泡排序中数据的交换操作:
if (a[j] > a[j+1]) { // 交换
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = true;
}
插入排序中数据的移动操作:
if (a[j] > value) {
a[j+1] = a[j]; // 数据移动
} else {
break;
}有了上面的理论,自己对两种排序方式进行测试
数据规模为1万时,性能差距是9倍;
数据规模为十万时,性能差距是20倍;
数据规模再增加量级时,由于耗时太长,我等不了,怕等到了天荒地老,所以就没有对比数据了。。。
/**
* 插入排序 VS 冒泡排序
*
* 做不同量级的数组,相同的机器配置,执行 {@link InsertionSortVsBubbleSort#insertionSortVsBubbleSort()} ,执行结果为:
* arrayByInsertion length = 100000 排序花费时间为:765
* arrayByBubble length = 100000 排序花费时间为:14366
*
* arrayByInsertion length = 10000 排序花费时间为:17
* arrayByBubble length = 10000 排序花费时间为:155
*
* 冒泡排序 插入排序
* 一万性能差【9】倍 155 17
* 十万性能差【20】倍 765(或1017) 14366(或19166)
* 百万耗时太长,我等不到结果
*
* @author kevin
* @date 2021/2/21 23:53
* @since 1.0.0
*/
public class InsertionSortVsBubbleSort {
public static void insertionSortVsBubbleSort() {
int dataLength = 10000;
int[] arrayByInsertion = new int[dataLength];
int[] arrayByBubble = new int[dataLength];
Random random = new Random();
for (int i = 0; i < dataLength; i++) {
int value = random.nextInt();
arrayByInsertion[i] = value;
arrayByBubble[i] = value;
}
long start = System.currentTimeMillis();
insertionSort(arrayByInsertion);
long end = System.currentTimeMillis();
long insertionTime = end - start;
BubbleSort.bubbleSort(arrayByBubble);
long end2 = System.currentTimeMillis();
long bubbleTime = end2 - end;
System.out.println("arrayByInsertion length = " + arrayByInsertion.length + " 排序花费时间为:" + insertionTime);
System.out.println("arrayByBubble length = " + arrayByBubble.length + " 排序花费时间为:" + bubbleTime);
}
}