七大经典排序算法总结【详解】
排序算法的分类:
一、插入排序(初始数据越接近有序,时间效率越高):
1、直接插入排序:
直接插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法(这就跟我们打扑克牌一样,选择一张扑克牌直接插入到前面已经有序扑克牌后面)。
(1)思路分析:
① 从第一个元素开始,该元素可以认为已经被排序
② 取出下一个元素,在已经排序的元素序列中从后向前扫描
③如果该元素(已排序)大于新元素,将该元素移到下一位置
④ 重复步骤③,直到找到已排序的元素小于或者等于新元素的位置
⑤将新元素插入到该位置后
⑥ 重复步骤②~⑤
(2)动图演示:
具体代码实现:
public static void insertSort(int[] array) {
int temp = 0;
for (int i = 0; i < array.length; i++) {
//选择一个数作为被比较的数;
temp = array[i];
int j = i - 1;
for (j = i - 1; j >= 0; j--) {
//取被比较数之前的数与被比较数进行比较;
if (array[j] > temp) {
//如果这个数大于被比较的数,往后挪一个位置;
array[j + 1] = array[j];
} else {
break;
}
(3)性能分析:
①平均时间复杂度:O(N^2)
②最差时间复杂度:O(N^2)
③空间复杂度:O(1)
④稳定性:稳定
2、希尔排序:
希尔排序(ShellSort)是对插入排序最坏的情况的改进,主要是减少数据移动次数,增加算法的效率。
(1)思路分析:
将要排序的序列按照步长gap进行分组,先在这几组内进行插入排序,之后再进行整体的插入排序,gap步长的选择是希尔排序最重要的部分,要保证最后一次排序的步长为1,这样就会保证整个数组将会被排序,并且步长必须小于数组长度。
(2)图片演示:
public static void shellSort(int[] array) {
//gap是为了分组;
int gap = array.length;
while (gap > 1) {
//下一次的组数是上一次的一半;
gap /= 2;
shell(array, gap);
}
}
public static void shell(int[] array, int gap) {
int temp = 0;
for (int i = gap; i < array.length; i++) {
//同一组数的第二个数;
temp = array[i];
int j = i - gap;
//同一组数的第一个数;
for (j = i - gap; j >= 0; j -= gap) {
if (array[j] > temp) {
array[j + gap] = array[j];
} else {
break;
}
}
array[j + gap] = temp;
}
}
性能分析:
①最好情况:时间复杂度为O(n)
②最坏情况下:时间复杂度为O(n^2)
③空间复杂度为:O(1)
④稳定性:不稳定
二、选择排序:
1、选择排序
(1)思路分析:
选择排序原理即是,遍历元素找到一个最小(或最大)的元素,把它放在第一个位置,然后再在剩余元素中找到最小(或最大)的元素,把它放在第二个位置,依次下去,完成排序。
(2)动图演示:
(3)具体代码实现:
public static void selectSort(int[] array) {
int temp = 0;
//记录此时最小的数;
int minIndex;
for (int i = 0; i < array.length; i++) {
minIndex = i;
int j = i + 1;
//找到最小的数;
for (j = i + 1; j < array.length; j++) {
if (array[minIndex] > array[j]) {
minIndex = j;
}
}
//将最小的数放到前面;
temp = array[i];
array[i] = array[minIndex];
array[minIndex] = temp;
}
}
(4)性能分析:
(1)时间复杂度:O(n^2;
(2)空间复杂度:O(1;
(3)稳定性:不稳定;
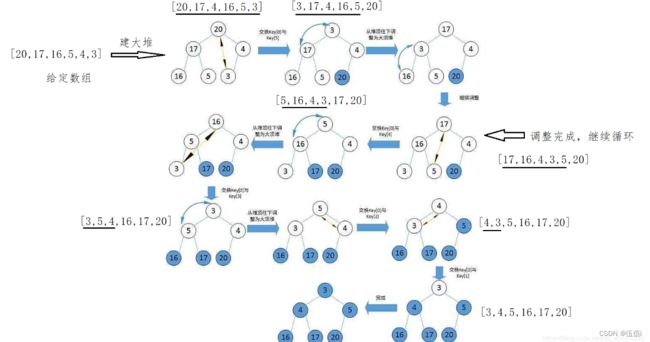
2、堆排序
堆是一个按照完全二叉树存储的数组,它是一个近似的完全二叉树但是同时它又满足堆的性质。
(1)思路分析:
.从小到大排序建大堆,从大到小排序建小堆
把堆顶的元素和当前堆的最后一个元素交换
堆的元素个数减一
从根节点向下调整
(2)图片演示:
(3)具体代码演示:
public static void heapSort(int[] array) {
creatBigHeap(array);
int end = array.length - 1;
while (end > 0) {
swap(array, 0, end);
shiftDown(array, 0, end);
end--;
}
}
//建立大根堆;
private static void creatBigHeap(int[] array) {
for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {
shiftDown(array, parent, array.length);
}
}
//向下调整;
private static void shiftDown(int[] array, int parent, int len) {
int child = 2 * parent + 1;
while (child < len) {
//找出最大孩子节点;
if (child + 1 < len && array[child] < array[child + 1]) {
child++;
}
//调整成大根堆;
if (array[child] > array[parent]) {
swap(array, child, parent);
parent = child;
child = 2 * parent + 1;
} else {
break;
}
}
}
//交换两个元素;
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
(4)性能分析:
(1)最好情况下时间复杂度为:O(nlogn)
(2)最坏情况下时间复杂度为:O(nlogn)
(3)空间复杂度为:O(1)
(4)稳定性:不稳定
三、交换排序
1、冒泡排序:
冒泡排序和选择排序差不多,都是与后面挨个比较,将最小的放到前面。
(1)思路分析:
冒泡排序是一种简单的排序算法,它不断地重复遍历数组,每次与其相邻的数进行比较,如果他们的顺序错误就交换,直到数组只剩下一个元素的时候,说明该数组已经排好序,之所以成为冒泡排序,是因为越小的元素会经由交换慢慢“浮”到数列的前面。
(2)动图分析:
(3)具体代码分析:
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length; i++) {
boolean flg=false;
for (int j = 0; j < array.length - 1 - i; j++) {
if (array[j] > array[j+1]) {
swap(array,j,j+1);
flg=true;
}
}
if(flg==false){
return;
}
}
}
(4)性能分析:
(1)最坏情况时间复杂度为:O(n^2)。
(2)平均情况时间复杂度为:O(n^2)。
(3)需要额外空间:O(1)。
(4)稳定性:稳定。
2、快速排序(重点)
快速排序是目前应用最广,最有意思的一个排序算法,速度快,空间利用率高,名副其实是理想中最快的算法了。
基本思想
这里是引用选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描,将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。
(1)挖坑法:
(1.1)基本思路:
①设置基准值,也就是数组的第一个元素。
②先将temp所在的位置设置为坑,然后从left开始找比temp大的数,找到后填上刚才temp处所设的坑,并且将找到的最大数的位置设为坑。
③end开始找比key小的数放到刚才最大数位置所设的坑处。
④这样就将数组分为两个子区间,如此循环。
(1.2)动图分析:
(1.3)具体代码实现:
public static void quickSort(int[] array){
quick(array,0,array.length-1);
}
public static void quick(int[] array,int start,int end){
if(start>=end){
return;
}
//找基准;
int pivot=partition(array,start,end);
//划分基准左边的数;
quick(array,start,pivot-1);
//划分基准右边的数;
quick(array,pivot+1,end);
}
public static int partition(int[] array,int left,int right){
int tmp=array[left];
//从右边找比temp小的值;
while (left<right){
while (left<right&&array[right]>=tmp){
right--;
}
array[left]=array[right];
//从左边找比temp大的值;
while (left<right&&array[left]<=tmp){
left++;
}
array[right]=array[left];
}
array[left]=tmp;
return left;
}
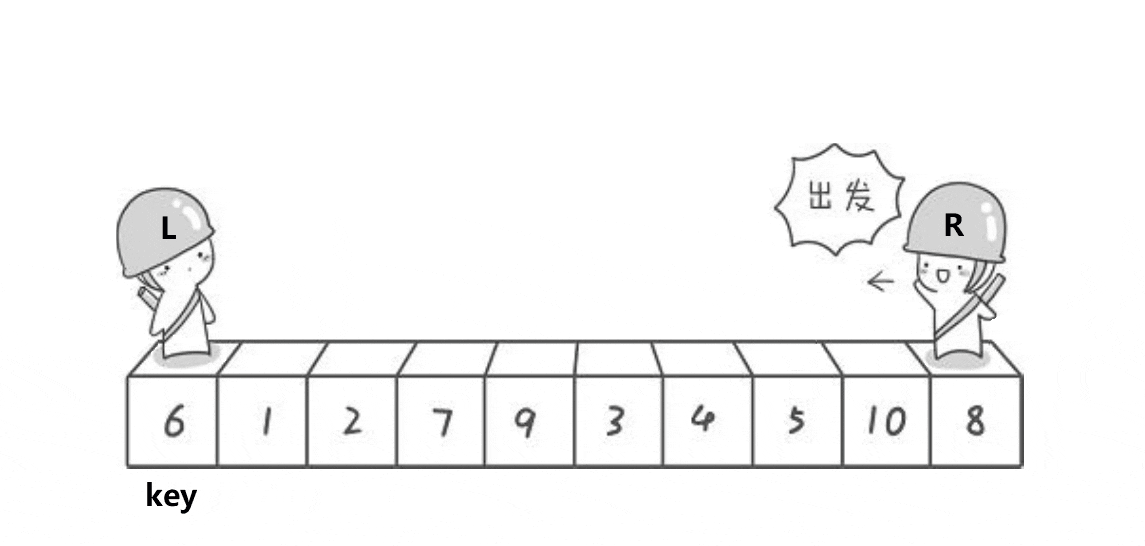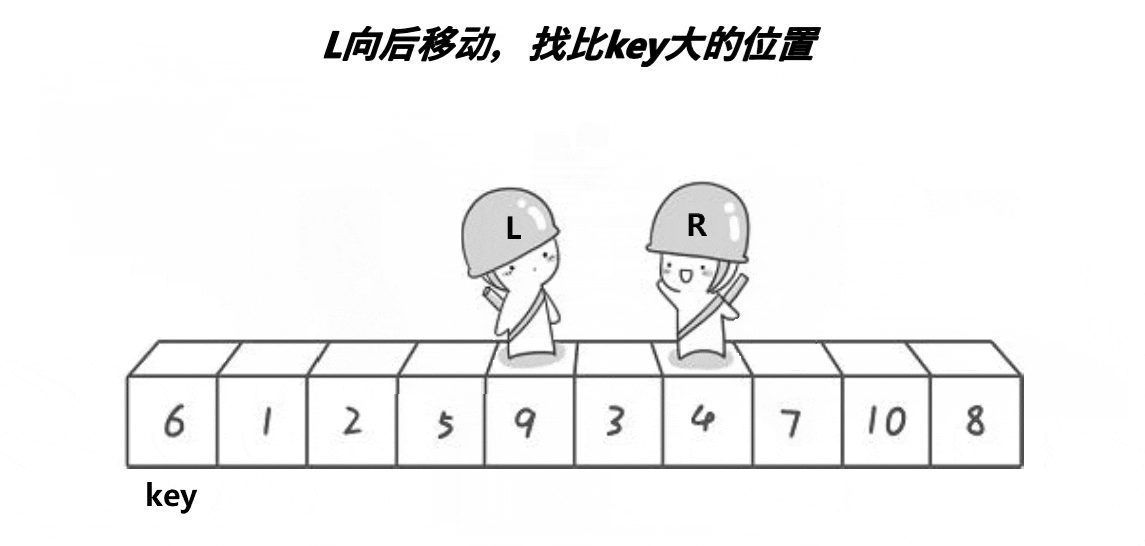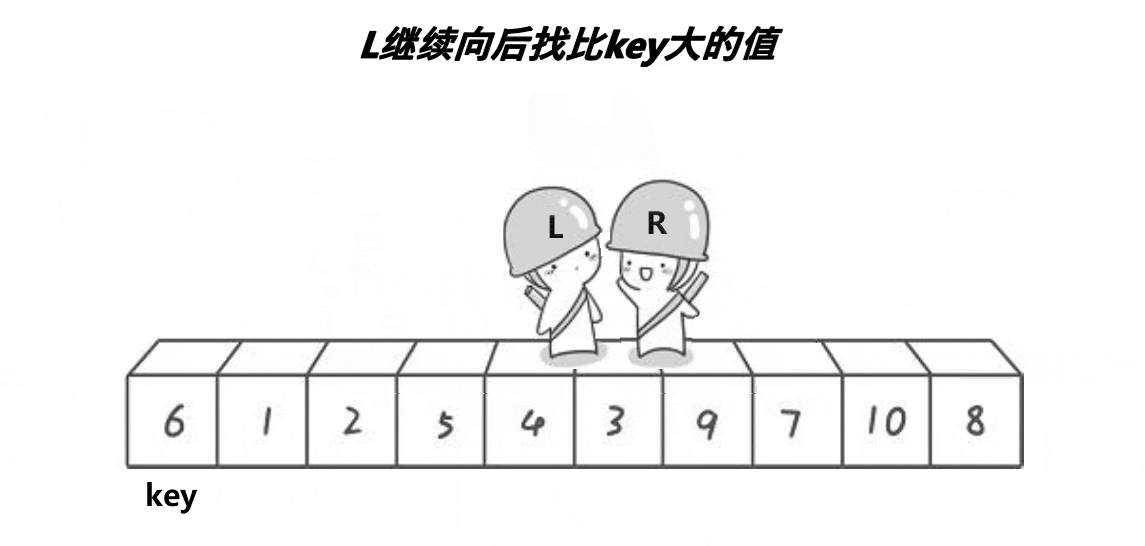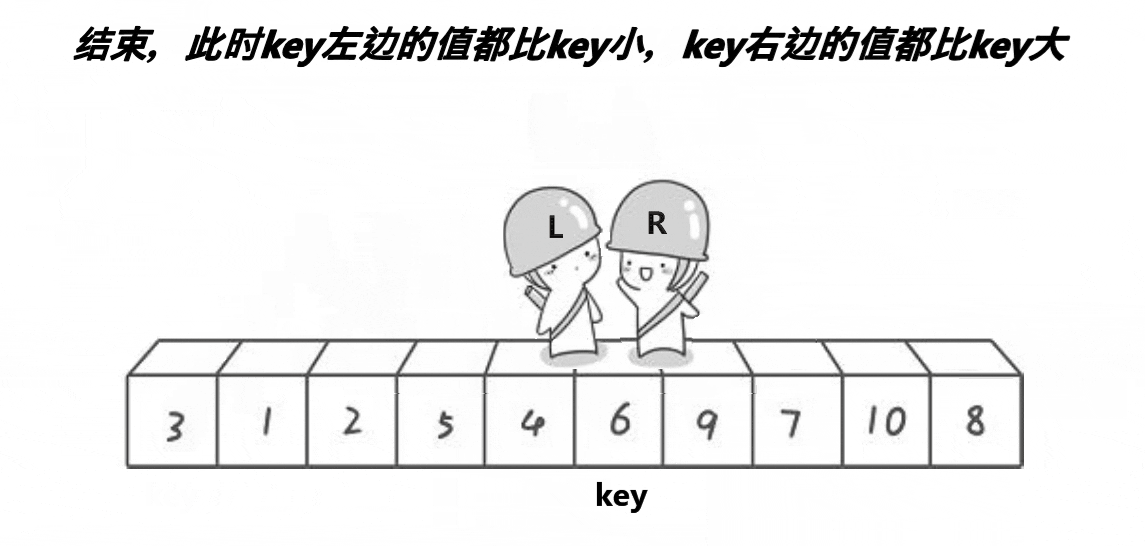
(2)Hoare法:
(2.1)基本思路:
①将左边设为temp;
②先从右边开始找比temp小的,再从左边开始找比temp大的,然后将两个交换。重复此步骤;
③left和right相遇,将left和temp交换;
(2.2)动图分析:
(2.3)基本代码实现:
public static void quickSort(int[] array){
quick(array,0,array.length-1);
}
public static void quick(int[] array,int start,int end){
if(start>=end){
return;
}
//找基准;
int pivot=partition2(array,start,end);
//划分基准左边的数;
quick(array,start,pivot-1);
//划分基准右边的数;
quick(array,pivot+1,end);
}
public static int partition2(int[] array,int left,int right){
int temp=array[left];
int i=left;
while (left<right){
//从右边找比temp小的值;
while (left<right&&array[right]>=temp){
right--;
}
//从左边找比temp大的值;
while (left<right&&array[left]<=temp){
left++;
}
//交换left和right的值;
swap(array,left,right);
}
swap(array,left,i);
return left;
}
//交换两个元素;
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
(3)前后指针法:
(3.1)基本思路:
①定义两个指针前后开始遍历;
②当后面的指针的值小于temp,并且它不等于前一个指针的下一个,交换两个值;
③当一个指针到达最右边,最后交换前一个指针和temp的值;
(3.2)动图分析:
(3.3)具体代码分析:
public static void quickSort(int[] array) {
quick(array, 0, array.length - 1);
}
public static void quick(int[] array, int start, int end) {
if (start >= end) {
return;
}
//找基准;
int pivot = partition2(array, start, end);
//划分基准左边的数;
quick(array, start, pivot - 1);
//划分基准右边的数;
quick(array, pivot + 1, end);
}
public static int partition3(int[] array, int left, int right) {
int prev = left;
int cur = left + 1;
while (cur <= right) {
if (array[cur] < array[left] && array[++prev] != array[cur]) {
swap(array, cur, prev);
}
cur++;
}
swap(array, prev, left);
return prev;
}
//交换两个元素;
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
(4)性能分析:
(1)时间复杂度:最好情况:O(n*logn);
最坏情况: O(n^2);
(2)空间复杂度:最好情况:O(logn);
最坏情况:O(n);
(3)稳定性:不稳定;
四、归并排序
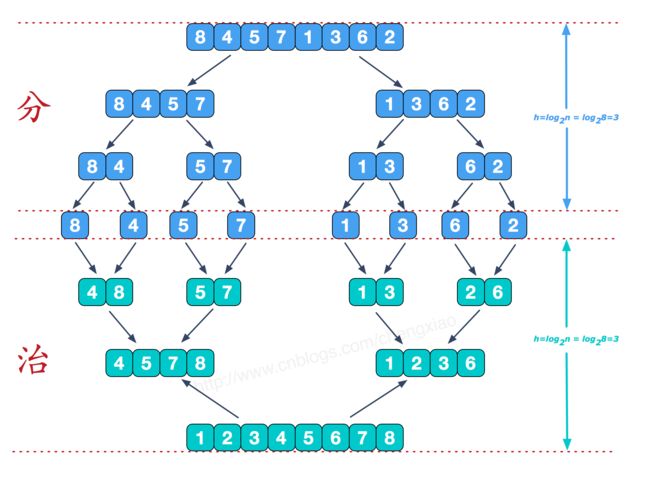
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
1、思路分析:
(1)分解(Divide):将n个元素分成个含n/2个元素的子序列。
(2)解决(Conquer):用合并排序法对两个子序列递归的排序。
(3)合并(Combine):合并两个已排序的子序列已得到排序结果。
2、图解分析
3、具体代码实现:
public static void mergeSort(int[] array){
mergeSortFunc(array,0,array.length-1);
}
//将左右分解;
public static void mergeSortFunc(int[] array,int left,int right){
if(left>=right){
return;
}
//取中间的数;
int mid=(left+right)/2;
//递归mid左边的数;
mergeSortFunc(array,left,mid);
//递归mid右边的数;
mergeSortFunc(array,mid+1,right);
merge(array,left,right,mid);
}
//将左右排序后进行合并;
public static void merge(int[] array,int start,int end,int mid){
int s1=start;
int s2=mid+1;
int[] temp=new int[end-start+1];
int k=0;
while (s1<=mid&&s2<=end){
if(array[s1]<=array[s2]){
temp[k++]=array[s1++];
}else {
temp[k++]=array[s2++];
}
}
while (s1<=mid){
temp[k++]=array[s1++];
}
while (s2<=end){
temp[k++]=array[s2++];
}
for (int i = 0; i <temp.length ; i++) {
//因为array不一定是从0开始所以要加start;
array[i+start]=temp[i];
}
}
4、性能分析:
(1)时间复杂度:O(n*logn);
(2)空间复杂度:O(n);
(3)稳定性:稳定;
五、排序算法总结:
1、应用场景:
数据量规模较小,考虑插入或选择。当元素分布有序时插入将大大减少比较和移动记录的次数,如果不要求稳定性,可以使用选择,效率略高于插入;
数据量规模中等,使用希尔排序;
数据量规模较大,考虑堆排序(元素分布接近正序或逆序)、快速排序(元素分布随机)和归并排序(稳定性);
一般来说不使用冒泡。