数据结构与算法--二叉搜索树2(递归)

代码随想录day23

文章目录

• 一、修剪二叉搜索树
• 二、将有序数组转换为二叉搜索树
• 三、把二叉搜索树转成累加树

---

一、修剪二叉搜索树

力扣题目链接669

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

提示：

  树中节点数在范围 [1, 104] 内
  0 <= Node.val <= 104
  树中每个节点的值都是 唯一 的
  题目数据保证输入是一棵有效的二叉搜索树
    0 <= low <= high <= 104

做题思路：此题也是采用递归的方法，做题之前想清楚递归的三个条件；1：确定递归函数的参和返回值 TreeNode trimBST(TreeNode root, int low, int high)   2：确定终止条件 if (root == null)  return null; 3：确定单层递归的逻辑  root.left = trimBST(root.left, low, high);  root.right = trimBST(root.right, low, high);

   下面几题都使用该步骤。

思路：如上图所示,先看根节点的左子树，当root.val

/**这是定义好的二叉树结构
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) {
            return null;
        }
        if (root.val < low) {
            return trimBST(root.right, low, high);
        }
        if (root.val > high) {
            return trimBST(root.left, low, high);
        }
        // root在[low,high]范围内
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}

---

二、把有序数组转换成二叉搜索树

力扣题目108链接

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

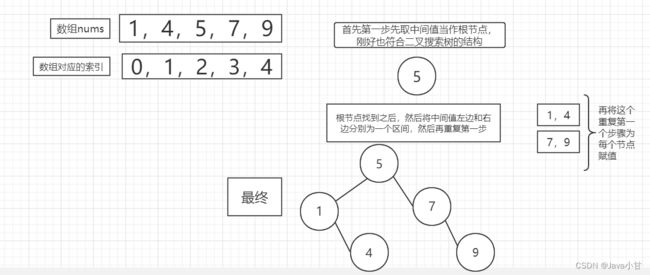
 思路：

上面就是这道题的具体思路，详细看代码

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
         return sb(nums,0,nums.length-1);
    }
    public TreeNode sb(int[] nums,int left,int right){
        if(left>right){
            return null;
        }
      int mid=left+(right-left)/2;//这里不能使用（left+right）/2，left和right都是最大int可
      //能会越界
     TreeNode root=new TreeNode(nums[mid]);
     root.left=sb(nums,left,mid-1);
     root.right=sb(nums,mid+1,right);
     return root;

    }
}

 

---

三、将二叉搜索树转换成累加树

力扣题目538链接

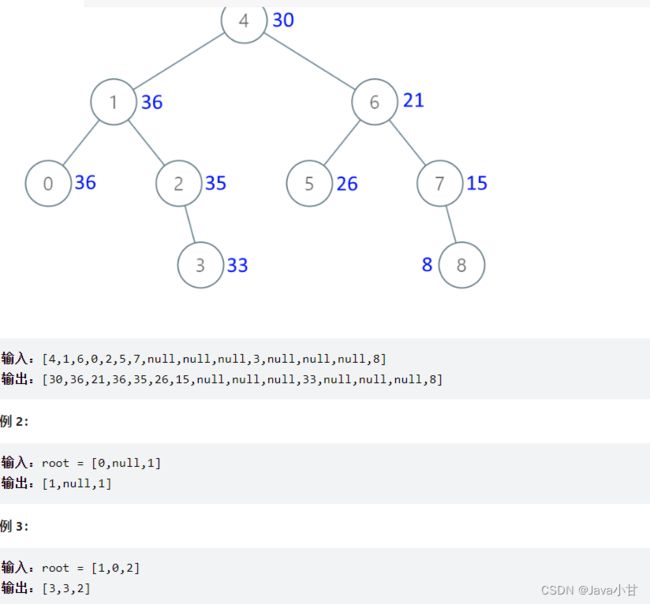
给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。

提示：

• 树中的节点数介于 0 和 104 之间。
• 每个节点的值介于 -104 和 104 之间。
• 树中的所有值 互不相同 。
• 给定的树为二叉搜索树。

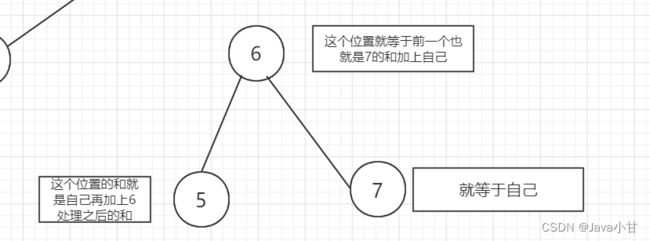
这题采用右中左的递归遍历顺序，因为数值大的在右边，先给右边的大的累加上，因为题中说的比自己大的或者等于的都得加上，所以先遍历右边。

 代码如下

class Solution {
    int sum；
    public TreeNode convertBST(TreeNode root) {
       sum=0;
       return  convertBST1(root);
       
    }
    public TreeNode convertBST1(TreeNode root){
        if(root==null){
            return null;
        }
        convertBST1(root.right);
        sum +=root.val;
        root.val=sum;
        convertBST1(root.left);
        return root;
    }

}

---