python与机器学习1,机器学习的一些基础知识概述(完善ing)
目录
1 AI ,ML,DL,NN 等等概念分类
1.1 人工智能、机器学习、深度学习、神经网络之间的关系:
1.2 人工智能的发展
2 ML机器学习的分类:SL, USL,RL
2.1 机器学习的分类
2.2 具体的应用举例
2.3 数据分类
3 关于阈值θ和偏移量b的由来
4 不同的激活函数
5 关于回归
6 关于分类
7 关于误差和梯度下降
8 最小二乘法修改θ
9 和矩阵计算,矩阵内积点乘的关系
10 深度学习
11 参考书籍
1 AI ,ML,DL,NN 等等概念分类
1.1 人工智能、机器学习、深度学习、神经网络之间的关系:
- 人工智能(Artificial Intelligence)是研究使计算机来模拟人的某些思维过程和智能行为(如学习、推理、思考、规划等)的学科。
- 机器学习(Machine Learning)是一门人工智能的科学,该领域的主要研究对象是人工智能,特别是如何在经验学习中改善具体算法的性能。
- 深度学习(Deep Learning)是机器学习领域中一个新的研究方向,它被引入机器学习使其更接近最初的目标——人工智能。
- 神经网络(Neural Network)是一种模拟人脑的神经网络以期望能够实现类人的人工智能机器学习技术,它是深度学习的基础。
下面这个图,是来自吴恩达的图
1.2 人工智能的发展
- 老的AI,逻辑
- 中间AI,
- 现在AI,数据
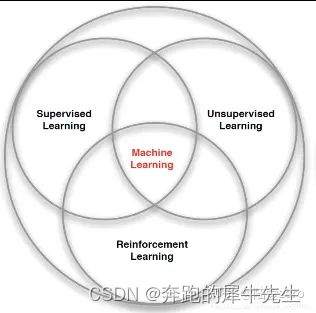
2 ML机器学习的分类:SL, USL,RL
2.1 机器学习的分类
- 监督学习(Supervised Learning): 教计算机如何去完成任务。它的训练数据是有标签的,训练目标是能够给新数据(测试数据)以正确的标签。
- 无监督学习(Unsupervised Learning):让计算机自己进行学习。它的训练数据是无标签的,训练目标是能对观察值进行分类或者区分等。
- 强化学习(Reinforcement Learning):智能体以“试错”的方式进行学习,通过与环境进行交互获得的奖赏指导行为,目标是使智能体获得最大的奖赏
2.2 具体的应用举例
- 监督学习算法:线性回归、Logistic回归、神经网络、支持向量机等。
- 回归,regression,用来预测连续值的输出,用来处理连续数据,如事件序列数据,比如按天记录的数据
- 分类,classification,是预测离散值输出
- 无监督学习算法:聚类、降维、异常检测算法等。
- 聚类,clustering,是无监督学习,训练数据无标签
- 特殊算法:推荐算法等。
下面这个图,是来自吴恩达的图
2.3 数据分类
- 数据分为2部分
- 一部分训练数据
- 一部分,验证数据
3 关于阈值θ和偏移量b的由来
比如很多信息传入可以表达为
- WX=w1x1+w2x2+....+wnxn
- 其中w表示权重,x表示信息/输入信息,n表示输入信息个数
- 也有的写成 θX=θ1x1+θ2x2+....这个是输入值,都是一个意思
从神经网络的模型来说
如果w1x1+w2x2+....>θ 就会激活
如果w1x1+w2x2+....<=θ 就不激活那么 w1x1+w2x2+....=θ就是判断公式
可以变形为
w1x1+w2x2+....=θ
w1x1+w2x2+....-θ=0
而尽量都取正数,就是
w1x1+w2x2+....+(-θ)=0
用系数b代替-θ
w1x1+w2x2+....+b=0所以这个b就可以认为是偏移量,
如果把b看成一个虚拟的输入信息,那么b的权重就是1
w1x1+w2x2+....+1*b=0w1x1+w2x2+....+w0*b=0
w0*b+w1x1+w2x2+....wnxn=0
转成矩阵形式
WT*X=0
转成点乘形式,W*X的内积点乘结果
W*X=w0*b+w1x1+w2x2+....wnxn
4 不同的激活函数
设置函数的结果在0-1之间,天生的符合概率的[0,1] 设计
一个最简单的函数,分段函数图形是直的,但是上下限也是[0,1]
- f(x)=0, if x<=0
- f(x)=1, if x>0
一个比较连续的, sigmod,分段函数图形是曲线,但是上下限也是[0,1]
sigmod,比较经典
- f(x)=1/(1-e^(-x))
- 其中 (e^(-x))' = -e^(-x) ,可以通过复合函数求导推出
为了不同情况下计算方便
还有的函数,分段函数图形是直的,但是上下限也是[-1,1]
- f(x)=1, if x>0
- f(x)=-1, if x<=0
类似的例子比如
1/2Σi=1~n(Yi-f(x)i)^2 ,加上1/2 就是为了微分结果导数更简单
5 关于回归
回归
线性回归,就是一次回归,表现为一条直线,包括1元,多元等1次回归
非线性回归,比如2次回归函数
- 有1次回归函数,其中包含1元的,2元等等,如果是多元的需要求偏导数
- 一般来说,一次回归函数都是线性函数
- 有2次回归函数,其中包含1元的,2元等等,如果是多元的需要求偏导数
- 一般来说,二次回归函数都是曲线
选择什么样的函数有差别,并不是 元的次数越高越好
- 如果函数次数太低,拟合不够,可以用精确度变化曲线,精确度和回归度比较
- 如果函数次数太高,可能是过拟合,可能训练数据拟合好,但是验证数据拟合不好,
6 关于分类
分类算法
- Logistic回归,是分类方法
- 线性可分
- 线性不可分(比如是曲线等)
假设W*X=w1x1+w2x2
如果W*X=w1x1+w2x2=0
假设w1 w2=1
x1+x2=0
W*X=|W||X|cosθ
其中cosθ 决定点乘内积符号 90-270,cos为负数,使得内积为负的向量
使得内积为正的向量
内积为正,两者相似
内积为负数,两者不相似
内积为0,两者垂直,完全不相关
分类是把 f(x) 做成了一个概率函数
可以看作是
- f θ(x)>0.5 时 y=1
- f θ(x)<=0.5 时 y=0
其实就是
- θTX>0 时 y=1
- θTX<=0 时 y=0
7 关于误差和梯度下降
误差函数,感觉很类似于方差函数
(y-f(x))^2
最梯度下降
采用最小二乘法? 可能会陷入局部最优
随机梯度下降
随机选择一些?一定能达到全局最优
随机梯度下降
最速下降,因为事先选取点的差别,可能陷入局部最优
而随机梯度下降,因为全局随机,理论上不会陷入局部最优,一定会找到全局最优
想象不规则的sinx这种函数曲线
1个随机数量
小批量随机梯度下降
8 最小二乘法修改θ
y=ax+b
y=θ0+θ1*x
根据一些原始数据,
大概200 → 500
但是随便假设θ0=1,θ1=2
fθ(x)=f(x)=y=1+2x
当时200 → 201
可见参数θ0=1,θ2=2 假设的不好
最小二乘法修改θ
E(θ)=1/2*∑(y-f(x))^2
E(θ)=1/2*∑(yi-f(x)i)^2
跟方差一样
还要去掉误差的正负影响,而是考虑误差与均值的差距的绝对值。
所以用平方
用平方,比abs更容易求导数
1/2也是为了求二次方的导数故意设计的,1/2或者2 只会改变函数形状的扁平还是高起,一般来说y=f(x) 值越大越高,值越小越扁平
所以最速下降法,就是求导数,也就是微分
导数函数求出来后,导数=0时的x 对应就是f(x)的极值
方法1 加上考虑函数的性质
比如 f(x)=x^2+2x+1这种往下凸出的,就是对应的最小值
方法2 比如 f(x)=x^2+2x+1 导数 f(x)'=2x+2
因此,最小值是x=-1对应
而且,
x>-1,f(x)'=2x+2>0 为正,f(x)递增
x<=-1,f(x)'=2x+2<0 为负,f(x)递减
所以
沿着与导数的符号相反的方向移动x,f(x) 就会朝着最小值前进
最速下降,梯度下降法
x=x-la*df(x)/dx
x=x-学习率*导数
学习率的选择要尽量小点,否则就会不容易收敛,或无法收敛
其实这就是更新的θ
如果f(x)=fθ(x1,x2,x3)=θ0+θ1*x+θ2*x^2 =θ*X
θ0=θ0-la*Σ(f(x)-y)
θ1=θ1-la*Σ(f(x)-y)x
θ2=θ2-la*Σ(f(x)-y)x^2
多变量,偏导数
如果f(x)=fθ(x1,x2,x3)=θ0*x0+θ1*x+θ2*x^2 =θ*X
变成2个向量点乘
9 和矩阵计算,矩阵内积点乘的关系
w1x1+w2x2+.....+wnxn
天生适合用矩阵计算
w1x1+w2x2+.....+wnxn=W*X
考虑到 偏移量(其实是和阈值有关系)
1*b+w1x1+w2x2+.....+wnxn=W*X
可变成
列向量 (1,w1,w2...wn) ,转行向量 (1,w1,w2...wn) T
列向量 (b,x1,x2...xn)
10 深度学习
输入层,中间层,输出层
中间层的宽度
中间层的层数,深度学习?
加宽度相对容易
加深度就会很难?
11 参考书籍
《机器学习的数学》
《深度学习的数学》
《程序员的AI书》