【数据结构】第一章——绪论（1）

导言

大家好，今天开始，我将开始从原先的专心学习C语言调整到边学习C语言，边学习数据结构的相关内容。
当然，在学习的过程中我也会将各个知识点通过博客记录下来并将自己对知识点的理解分享给大家。
本章内容是数据结构的概述，我们可以通过对本章内容的学习，初步了解数据结构的基本内容和基本方法。

一、基本概念和术语

1.数据

定义

数据是信息的载体，是描述客观事物属性的数、字符以及所有能输入到计算机中并被计算机程序识别和处理的符号的集合。数据是计算机程序加工的原料。

记忆定义

我对该定义的记忆方式是先抓主干，后补充细节。
主干：数据是一个载体，它也是一个集合，它更是一种原料。
细节：数据作为信息的载体，是描述客观事物属性的数、字符以及所有能输入到计算机中并被计算机程序识别和处理的符号的集合，是计算机程序加工的原料。

理解定义

我们可以简单的理解为，描述客观事物属性的相关信息是通过承载在数据上然后再被计算机程序加工，最后呈现在我们面前。

就比如这篇博客，呈现在我们面前的就是一些图文，这些图文呈现的步骤就是：

先通过我输入相应的字符，然后计算机在识别这些字符后通过一系列的处理，最终将这些信息呈现出来。

在C语言中我们学到了计算机能够识别的内容就是二进制序列，计算机能处理的内容也是二进制数列。下面我们通过流程图来理解这个过程：

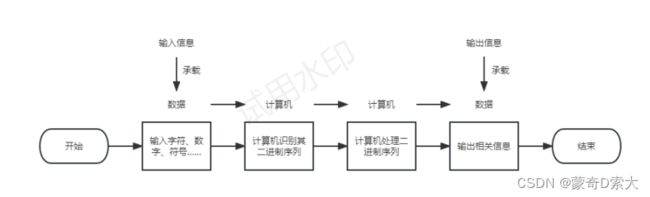
从图中我们应该能更好的理解数据以及它在计算机中的一个运行流程，这里我再进行一次文字解释：

我们在计算机上开始操作后，

• 首先是先将我们需要输入的信息通过字符、数字、符号等形式输入进计算机，此时我们输入的信息承载在数据上；
• 然后这些数据会将信息运送给计算机，计算机开始加工这些数据，加工的过程是先识别这些信息的二进制序列，再将这些二进制序列处理成我们想要的内容；
• 最后我们想要的这些内容作为需要输出的信息，将会再一次承载在数据上，通过数据，输送到我们的屏幕上进行输出。

☆☆☆我们输入和计算机输出的内容就是数据。

2.数据元素

定义

数据元素是数据的基本单位，通常作为一个整体进行考虑和处理。
一个数据元素可由若干个数据项组成，数据项是构成数据元素的不可分割的最小单位。

记忆定义

主干：数据元素是基本单位，通常作为一个整体进行考虑和处理。
细节：数据元素是数据的基本单位。这个整体可由若干个数据项组成，数据项是构成数据元素的不可分割的最小单位。

理解定义

下面我们通过画图来进一步理解数据、数据元素和数据项之间的关系：

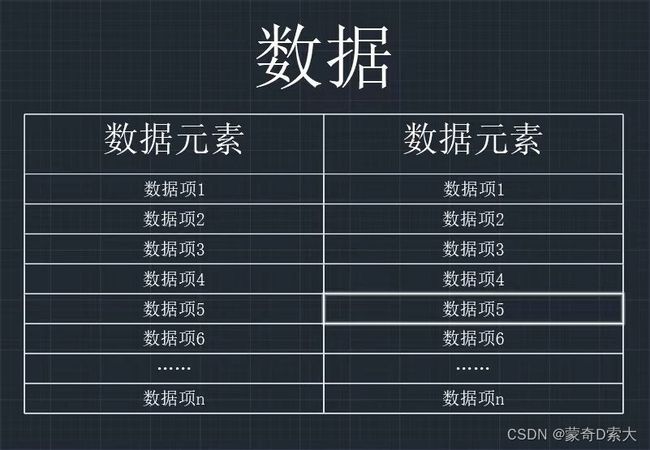
从图中可以看到，若干个数据项组成了一个整体，这个整体就是数据元素，然后由若干个数据元素组成了一个完整的数据。
这里我们举一个例子来加深一下对这个知识点的理解：

学校马上要开运动会了，现在班上要学生报名，并要求登记报名的项目、身高、体重。
总共有10人报名，张三报名了400m，李四报名了跳远、王五报名了铅球……

在这个例子中总人数就是班上运动会报名的数据，张三、李四、王五……这些学生就是一个个数据元素，他们报名的项目、身高、体重就是数据项。

• 数据描述的是一个集合，这个集合是由报名的学生组成的；
• 数据元素描述的是一个个体，这些个体就是张三、李四、王五……他们这些学生；
• 数据项指的是组成数据元素的不可分割的最小单位，这些数据项就是项目、身高、体重这3项内容；

如果一个数据项中的内容由多个属性组成，比如2020-10-19这个内容我们可以把它拆分为年月日，那这种情况下，这个数据项我们就把它称为组合项。

☆☆☆不可分割的数据项组成一个数据元素，所有数据元素的集合就是数据。

3.数据对象

定义

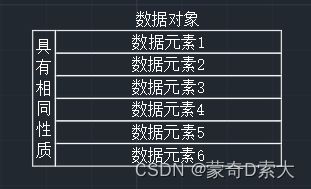
数据对象是具有相同性质的数据元素的集合，是数据的一个子集。

记忆定义

主干：数据对象是一个集合，是一个子集。
细节：数据对象是具有相同性质的数据元素的集合，是数据的一个子集。

理解定义

我们还是通过画图来理解：

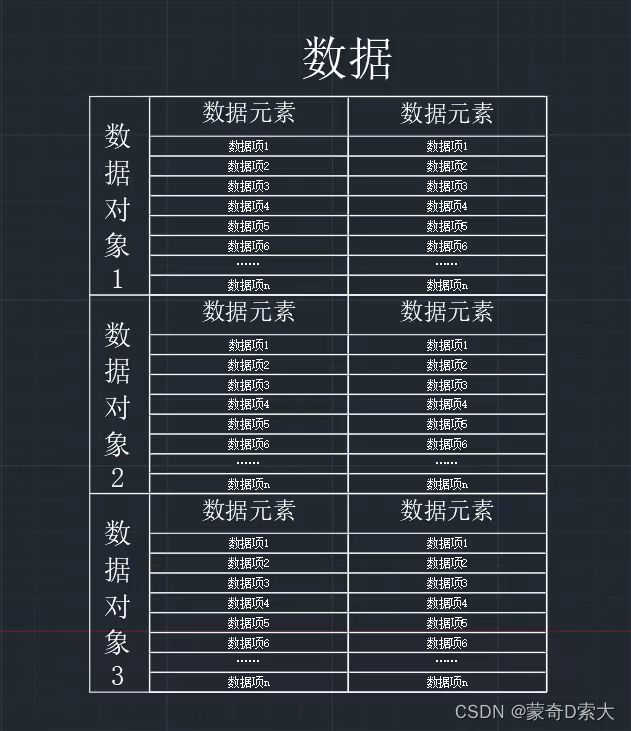
图中我们可以看到，这一整个集合组成了数据，两个数据元素组成了一个数据对象，n个数据项组成了一个数据元素。

要注意的是组成数据对象的两个数据元素要是相同性质的。

比如现在学校组织运动会，班级里要统计运动员、新闻稿、后勤员等工作的名单。

• 所有的运动员的学生名单组成的集合就是一个数据对象；
• 所有写新闻稿的学生名单组成的集合就是第二个数据对象；
• 所有的后勤员的学生名单组成的集合就是第三个数据对象。

☆☆☆数据项的集合是一个数据元素，相同性质的数据元素的集合是一个数据对象，所有数据对象的集合是数据。

4.数据结构

定义

数据结构是相互之间存在一种或多种特定关系的数据元素的集合。

记忆定义

主干：数据结构是集合。
细节：数据结构是数据元素的集合，这些数据元素相互间存在一种或多种特定关系。

理解定义

数据结构是由数据和结构组成。
数据也就是指的数据元素，结构就是指的数据元素相互之间的关系。

数据结构与数据对象

数据结构和数据对象一样，也是数据元素的集合，但是两者的区别是：

数据对象只需要数据元素之间有相同的性质；

如图所示：

在这个例子中，数据元素1~6它们之所以能构成数据对象，是因为它们具有相同的性质，这里我们简单的理解为它们都是白色字体，白色字体就是它们的相同性质；

数据结构则需要数据元素之间存在特定的关系；

如图所示：

在这个例子中，数据元素1~4它们构成了一个数据结构，因为它们相互之间满足一种特定的关系，这里我们简单的理解为就是它们之间都有向下的指向的线性结构；

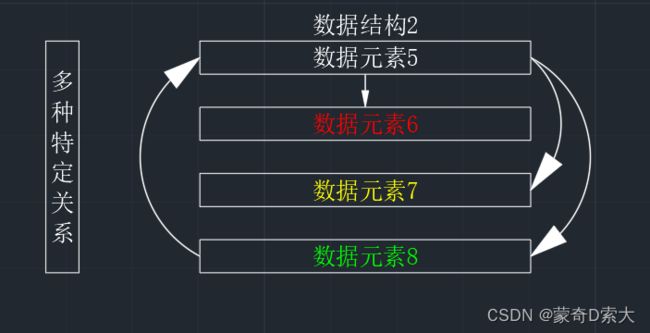
在这个例子中，对于数据元素5来说，它和数据元素6、数据元素7、数据元素8之间具有多种关系：
和数据元素6与数据元素7它们具有的是从5指向6和7的放射状结构；
和数据元素8它们具有的是从5指向8 ，8指向5的闭合结构；

☆☆☆由相互之间存在一种或多种特定关系的数据元素组成的集合就是数据结构。

5.数据类型

定义

数据类型是一个值的集合和定义在此集合上的一组操作的总称。

记忆定义

主干：数据类型是一个集合和总称。
细节：数据类型是一个值的集合和定义在此集合上的一组操作的总称。

分类

原子类型

原子类型是指其值不可再分的数据类型。
如布尔类型、char/short/int/long/long long/float/double……像这种已经不可再分的数据类型就是原子类型；

结构类型

结构类型是指其值可以再分解成若干成分（分量）的数据类型。
如结构体数据类型、枚举数据类型……像这种我们可以继续细分的数据类型就是结构类型；

抽象数据类型(Abstract Data Type, ADT)

抽象数据类型是指抽象数据组织及与之相关的操作。
我们在定义一个ADT时，需要确定两件事情：

1. 确定抽象数据元素以及这些抽象数据元素之间有什么样的关系，它们是怎么样组织的，这就是在“定义”一种数据结构；
2. 确定对于这些数组元素可以执行什么样的操作；

理解定义

在知道了数据类型的分类后，我们来通过具体的例子来理解数据类型的定义；

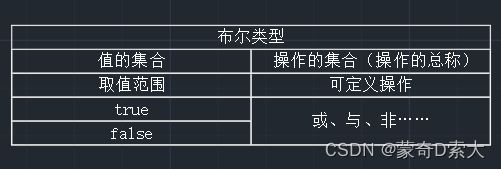
原子类型

在布尔类型中：

它的值的范围为true、false，也就是说布尔类型是true和false这两个值组成的一个值的集合；
我们对布尔值可进行的操作有：或、与、非……，也就是说布尔类型是定义在这个值的集合上的一组操作的总称；

在int类型中：

它的值的范围为-2³¹~2³¹-1，也就是说int类型是这个范围内所有的值组成的一个值的集合；
我们对这些值可以进行的操作有：加、减、乘、除、模运算……，也就是说int类型是定义在这个值的集合上的一组操作的总称；

对于原子类型来说，它既是由值组成的一个集合，也是定义在这个集合上的一组操作的总称。

结构体类型

在结构体类型中，比如我们要描述一个学生的相关信息，我们可以定义一个如下所示的结构体类型：

//结构体数据类型
struct student//结构体类型
{
	char name[20];//姓名
	char std_ID[20];//学号
	double hight;//身高
	double weight;//体重
};

在这个结构体类型中

它是由姓名、学号、身高、体重这些子类型组成的一个集合；
我们可以对这个集合中的子类型进行的操作有：加、减、赋值、比较大小……

对于结构体类型来说，它既是由子类型所组成的一个集合，也是定义在这个集合上的一组操作的总称。

抽象数据类型

在抽象数据类型中，比如福布斯中国内地富豪榜：

排名	姓名	财富（美元）
1	钟睒睒	623
2	张一鸣	495
3	曾毓群	289
4	马化腾	234
5	马云	206
6	王卫	196
7	何亨建	188
8	丁磊	187
9	黄峥	186
10	秦英林	184

在这些抽象数据元素中，这些数据元素直接可以根据不同的条件形成不同的组织，比如根据它们的财富总额进行的排名，这就是一种关系，他们这些数据元素依靠这种关系形成了一个组织，也就是富豪排行榜；

我们可以对他们这些元素进行重新排名、给他们的位置进行调换、修改他们的财富值、删除其中的某个元素或者插入某个元素，这些都是我们可以给这些数据元素定义的操作；

对于抽象数据类型来说，它既是抽象元素所组成的一个集合，也是定义在这个集合中的操作的总称。

总结

从上述例子中我们可以对数据类型的定义来进行进一步的理解：

数据类型是由值的集合与操作的集合这两个子集所组成的集合；

数据项、数据元素以及数据对象的一一对应如下图所示：

在数据类型的值中：

数据类型取值范围内的值也就是一个一个的数据项；
这些数据项组成了值的集合这个数据元素；
值的集合单独构成了一个数据对象1；

在数据类型的操作中：

对这些值可定义的操作也是一个一个的数据项；
这些数据项组成了操作的集合就是操作的总称这个数据元素；
操作的总称单独构成了一个数据对象2；
所以我们说数据类型是一个值的集合和定义在此集合上的一组操作的总称。

二、数据结构的三要素

在前面介绍数据结构时我们有提到了数据结构就是由数据元素和元素之间的特定关系组成 。
这种数据元素之间的特定关系称为结构。数据结构包括三个方面的内容：逻辑结构、存储结构和数据运算。
下面我们就来一一介绍这个三个内容；

1.数据的逻辑结构

定义

逻辑结构指的是数据元素之间的逻辑关系，即从逻辑关系上描述数据。它与数据结构的存储无关，是独立于计算机的。

分类

数据的逻辑结构分为线性结构和非线性结构，线性表示典型的线性结构；集合、树和图示典型的非线性结构。

集合

简单的理解为就是所有的数据元素同在一个圈子里，但是他们之间并没有其它的关系；
比如数学中我们学过的自然数的集合、有理数的集合、整数的集合、正整数的集合、负整数的集合……在这些集合中的元素，我们并不需要它们之间存在某种关系，只要满足集合的条件，它就能进入这个集合。如下图所示：

在这个集合中，集合里的元素只是满足了12以内的这个条件就进入了这个集合，元素之间有没有什么其它的关系并不重要；

线性结构

对于线性结构来说，数据元素之间是一对一的关系。
除了第一个元素，所有的元素都有唯一前驱；除了最后一个元素，所有元素都有唯一后继。如下图所示：

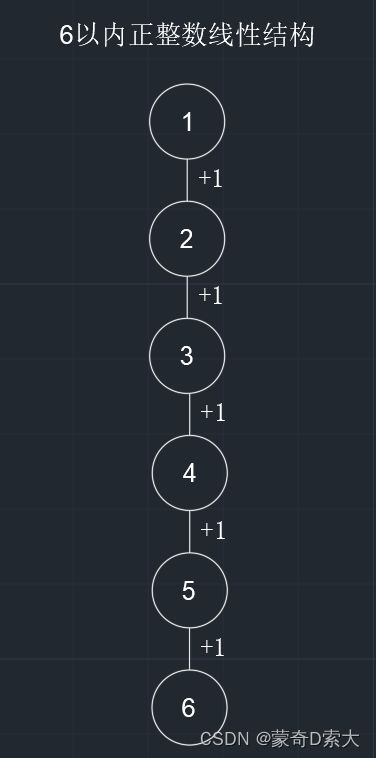
在这个线性结构中，元素之间的对应关系是差值为1；
在上图中我们可以看到两个元素之间是一对一的关系；
我可以通过元素2进行+1的操作能且仅能找到元素3，这就是唯一后继；
同时我也能通过元素3进行-1的操作能且仅能找到元素2，这就是唯一前驱；
但是我在这个结构中通过元素1进行-1的操作不能找到任何元素，这就是首元素没有前驱；
同理我通过元素6进行+1的操作也不能找到任何元素，尾元素没有后继；

树

对于树来说，数据元素之间是一对多的关系。

我们可以想象一下一棵树，它是由树干树枝树叶组成，每一棵树都只有一个树干，但是它可以有很多的树枝，每根树枝上又能有很多的树叶。

这里介绍的树就同一棵树一样，一个元素，它能与多个元素存在关系。

在日常生活中，这种结构是很常见的，比如一家公司的组织框架、计算机中的文件存放路径、我们记笔记时使用的思维导图、不同的产品及其分类……这些都是树结构。如下图所示：

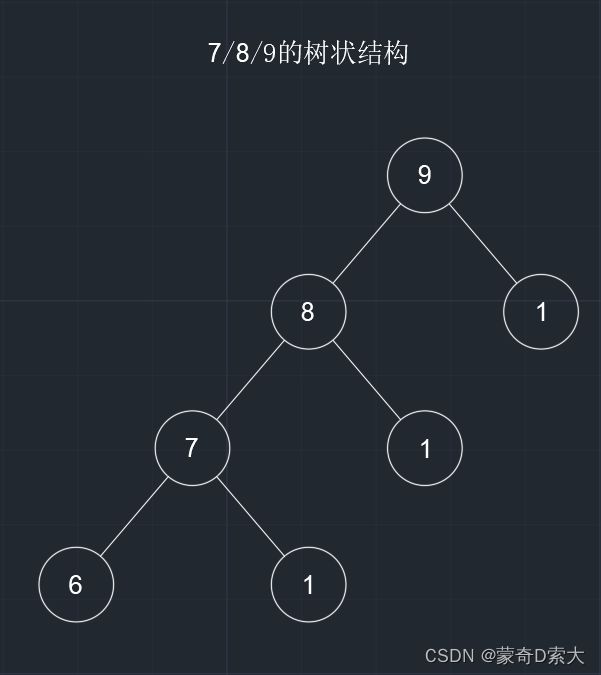
在这个树状结构中，元素之间的对应关系是分解成两个加数并且其中一个加数为1；
在上图中，我们可以看到每一个元素通过这个关系能得到两个元素，元素之间是一对多的关系；
元素9通过这个对应关系得到了元素1和元素8；
元素8通过这个对应关系得到了元素1和元素7；
元素7通过这个对应关系得到了元素1和元素6；

图

对于图来说，数据元素之间是多对多的关系。
图有称图状结构，也称为网状结构，就像蜘蛛网一样。如下图所示：

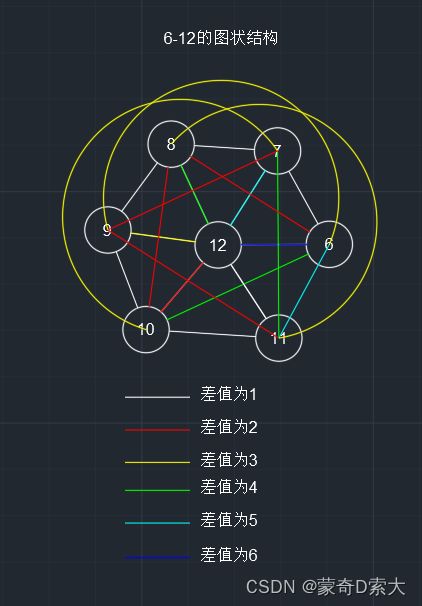
在这个图状结构中，元素之间的对应关系不唯一，有多个对应关系；
在上图中，我们可以看到每个元素通过这些对应关系都能得到多个元素，元素之间是多对多的关系；
元素12通过这些关系可以得到其它的所有元素；
元素11也能通过这些关系得到其它的所有元素；
同理，每个元素通过这些关系都能得到多个元素

2.数据的存储结构

定义

存储结构是指数据结构在计算机中的表示（又称映像），也称物理结构。它包括数据元素的表示和关系的表示。

分类

数据的存储结构是用计算机语言实现的逻辑结构，它依赖与计算机语言，数据的存储结构主要有顺序存储、链式存储、索引存储和散列存储。

顺序存储

定义

所谓的顺序存储就是把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中，元素之间的关系由存储单元的邻接关系来体现。

优缺点

其优点是可以实现随机存取，每个元素占用最少的存储空间；
缺点是只能使用相邻的一整块存储单元，因此可能产生较多的外部碎片。

链式存储

定义

不要求逻辑上相邻的元素在物理位置上也相邻，借助指示元素存储地址的指针来表示元素之间的逻辑关系。

优缺点

其优点是不会出现碎片现象，能充分利用所有存储单元；
缺点是每个元素因存储指针而占用额外的存储空间，且只能实现顺序存取。

索引存储

定义

在存储元素信息的同时，还建立附加的索引表。索引表中的每项称为索引项，索引项的一般形式是（关键字，地址）。

优缺点

其优点是检索速度快；
缺点是附加的索引表额外占用存储空间。

!!!另外，增加和删除数据时也要修改索引表，因而会花费较多的时间。

散列存储

定义

根据元素的关键字直接计算出该元素的存储地址，又称哈希（Hash）存储。

优缺点

其优点是检索、增加和删除结点的操作都很快；
缺点是若散列函数不好，则可能出现元素存储单元的冲突，而解决冲突会增加时间和空间开销。

3.数据的运算

施加在数据上的运算包括运算的定义和实现。运算的定义是针对逻辑结构的，指出运算的功能；运算的实现是针对存储结构的，指出运算的具体操作步骤。

结语

以上就是数据结构绪论的第一部分——数据结构的基本概念和三要素。
文章内容来自《王道考研系列——2024年数据结构考研复习指导》。
这里介绍了大量名词及名词定义，因为本书在第二章会讲解线性表、第五章会讲解树、第六章会讲解图，所以目前我们只需要了解这些基本的定义就可以了。多的内容我也还没学习到也无法为大家展开介绍。
接下来随着学习的深入，我会继续给大家介绍我在学习过程中的感受。最后感谢各位的翻阅，咱们下一篇再见。

博客同步声明

本文将同步至51CTO博客——蒙奇D索隆的博客中，博客地址：​​https://blog.51cto.com/u_16231477