【文献阅读-CSI NN】

【文献阅读】CSI NN: Reverse Engineering of Neural Network Architectures Through Electromagnetic Side Channel

Tips： 以下内容包含读者在阅读这篇逆向工程论文过程中写下的一些翻译，其中参杂个人对于这项工作的理解
原文链接：https://www.semanticscholar.org/paper/CSI-NN%3A-Reverse-Engineering-of-Neural-Network-Side-Batina-Bhasin/b12c15503435cffee16bdd156766dcf390eeb8f8

0、Abstract

• 对仅包含MLP和CNN的网络模型进行重建，目标芯片为ARM Cortex-M3
• 可以根据timing delay和EM，还原包括激活函数、层数、每层的节点数、权重、输出的类别在内的所有参数

1、Introduction

• 说了一下深度学习应用广泛，然后模型被嵌入到一些低功耗的芯片上，但是不轨分子可能会因此而窃取模型，或者通过训练模型而窃取训练集，这些都会危害知识产权，因此本文进行侧通道分析的研究，希望找到能够妨害的措施。

• 之后又提了不轨分子获得芯片后可以直接拆解从而获得其中的信息，但是有些公司也有相应的措施来将芯片制成一个黑盒，从而无法从物理层面拆解获得信息，因此，作者提出采用侧通道分析的方法进行还原模型。

• 侧通道分析主要由三种方法组成：时间延迟(timing delay/reaction time)、功率消耗、电磁辐射

1.1、 Related work

• 相关的一些工作有：轮廓侧通道攻击、模板攻击、密钥恢复攻击、缓存攻击

1.2、Contribution and organization

• 提出了完整的基于侧通道分析的逆向工程，可以重建模型关键参数比如：激活函数、初始权重、隐藏层数目、每个隐藏层的大小。并且不依赖于任何原始训练数据，仅仅需要对部分输入、输出信息，以及测量的侧通道信息
• 平台为8-bit的AVR和32-bit的ARM
• 处理实数的时候发现了一些有趣的结果，比如即使攻击失败也可以获得一些敏感信息，基于精度误差
• 提出了一些保护措施来抵御侧通道攻击

2、Background

• 先介绍一下所使用的几种网络：MLP、CNN，然后再讨论本文中运用的测通道攻击技术

2.1、Artificial Neural Networks

• 对ANN的一些简单介绍

2.1.1、Multilayer Perceptron

• 介绍了MLP的基本概念，每一个隐藏层中含有多个单元，每个节点对应于一个权值w，并且每个节点后面会有对应的一个激活单元

2.1.2、Convolutional Neural Network

• 卷积网络包含三种层：卷积层、池化层、全连接层

• 一层卷积层的权重即为那个卷积核，这一层使用这一个卷积核

• 池化层分为平均值池化和最大值池化

• 全连接层就是个全连接

2.1.3、Activation Functions

• 常见的激活函数有：ReLU、sigmoid、tanh、softmax

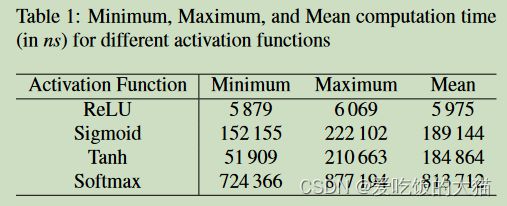
• ReLU的运行速度最快，因为他没有指数操作和除法操作，后面三个都包含指数和除法

2.2、Side-channel Analysis

• 测通道攻击相比于以前的其他方法的好处在于：分而治之，通过将网络分成不同的部分进行恢复
• Simple Eletromaganetic/Power Analysis(SEMA/SPA)，这是侧通道分析的最简单形式，例如SPA可以直接使用RSA算法从乘法运算中区分出平方运算，而本文用的SEMA也与此类似
• Differential Eletromaganetic/Power Analysis(DEMA/DPA)，这是侧通道分析更高级的形式，称之为差分电磁分析，处理的是实际输出信息与推测输出信息之间的差分关系，推测输出信息来源于一些模型的侧通道信息和关键假设，在这里作者说的关键假设其实就是权重，给定模型一些输入，乘以假设的权重，得到推测的输出信息，之后采用汉明model，计算实际输出和推测输出之间的汉明距离，来判断哪一个假设与实际的输出信息相关性更大，同时由于是采用汉明model，所有数据都被数值化为了0和1，一旦有偏差则会造成汉明距离有较大的差距，因此对SNR要求比较高，需要许多次测量求平均，数据量比SEMA更大

3、Side-channel based reverse engineering of neural networks

3.1、Threat model

Scenario

• 对象模型为MLP和CNNs
• 不假设输入的类型和来源，可以是整数也可以是浮点数
• 假设被测模型没有针对侧通道分析的抵御措施

Attacker’s capability

• 攻击的时候不会影响模型的正常运行
• 对模型的结构没有先验知识，不知道训练数据集
• 只能通过选择模型的输入input来控制芯片是否运行
• 可以测量输出、所需的侧通道信息，但不能测量模型运行中的某一个值
• 这通常被称为known-plaintext attack（已知明文攻击），即攻击者获得了这个网络的一个样品，带回家中做实验，这个样品是一个黑盒，仅能控制输入，观测输出，测量侧通道信息

3.2、Experiment setup

• 方法是基于Ateml ATmega328P平台提出的，后续在ARM Cortex-M3进行验证，测量工具为Lecroy WaveRunner 610zi 电子示波器，每一个输入input都能通过示波器得到output

• 后面inputs和traces都将表示同一个意思，都意味着一连串的输入/示波器的输出，信号的同步依靠传统的握手信号进行开始和停止

• 所测量的EM信号包含着time delay信息

• 系统总线都是从0开始初始化，当激活后，处理器会从存储单元加载数据到总线上，这时总线会从全0的序列变为有0有1的序列，换言之就是，消耗了多少功率/产生多少电磁辐射等效于1的比特数。

• 当模型从内存里加载一个预设的权重的时候，如果这个权重是由8位整形表示的，假设这个权重为x=[x7,x6,…,x0]，那么这个权重的汉明重量可以通过下面这个式子计算得到，这将被后续测通道分析中用来推算模型的真实权重（通过计算HW(xw)和HW(xw’)之间的互相关系数）

3.3、Reverse engineering the activation function

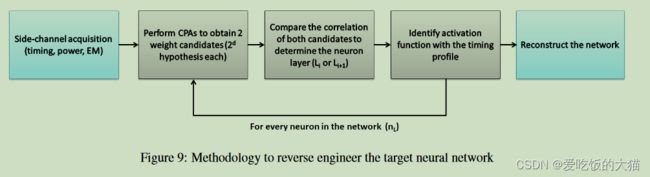
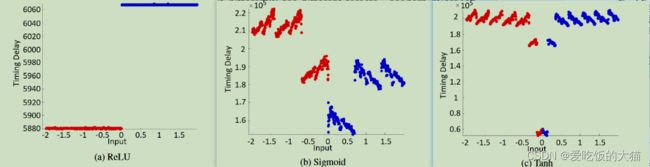
作者设置了输入x=[-2,2]，总共测了2000次EM数据，得出不同输入下，不同的激活函数对应的时间延迟，如下图所示：

作者从测量的EM信息中，分析出不同的激活函数带来的时延情况，如下所示：

作者提出，如果有必要的话，可以做一些模式匹配来确定用的是哪个激活函数

3.4、Reverse engineering the multiplication operation

使用correlation power analysis(CPA)来恢复权重，CPA即为上文中DPA的一个变种，对象是乘法操作m = x*w，基于皮尔逊相关系数ρ(t,w)来推测权重，相关系数大的w，可认为是与真实权重更接近，t为计算结果m存储回寄存器的时延

通过内存分析可以知道，模型运行乘法操作后，权重会从4个寄存器加载到总线上，每一个寄存器存放8位浮点数

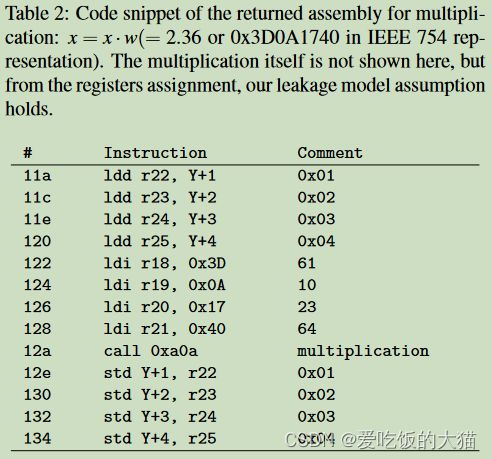
32位浮点的构成如下，b31为符号位，b30-b23为指数位，b22-b0为位数位：

具体的操作如下：

1. 设置输入x为[-1.00,1.00]之间的均匀分布
2. 设置预测权重w’为[-N,N]之间的均匀分布，精度p=0.01，作者取的N=5
3. 计算预测的乘法结果m’=x*w’,实际测量的输出结果为m
4. 将预测输出m’和实际输出m表示为一个32位浮点数的类型，分别对他们的符号部分、指数部分、位数部分进行计算汉明重量HW(m)和HW(m’)，分三次完成对一个权重w的预测
5. 对于一个输入x，有1000个w’与之相乘，对应则有1000个HW(m’)，计算HW(m)和HW)(m’)的皮尔逊相关系数，将相关系数最大的那个w’作为最终的预测权重

作者给出了上面这幅图，表示的是在预测权重w’为2.43时，前三位尾数（0、0、1）的相关系数与时间的对应关系，黑色表示的是预测为正确(|m(w’)-m(w)|<0.01)的权重的相关系数，即2.43对应的各个位尾数，而红色表示的是某一个错误预测权重的相关系数，比如w’'=2.83，它对应的尾数的第一位是1，那么看到这儿，我猜是可以画出下面这个表格的：

这个表格第一行全是1，第二行全是0，一共有23列，每一列代表着对某一位的尾数进行预测的情况，一位尾数只存在0和1两种情况，红色表示的是上图中画红线的意思，即相关系数小的那一种情况，灰色表示的是上图中画黑线的意思，即相关系数大的那一种情况，作者会对23位尾数的每一位都画出相关系数图，然后判断每一位是0还是1的可能性大，以此完成对权重的23位尾数的预测，例如在本例中前三位尾数中就是0、0、1的相关系数更大。

同时，作者称这些相关系数在时间上跨度很广的原因有两个，一个是测量的EM信息含有噪声，二是乘法操作不是瞬时的，是占据一个时间段的

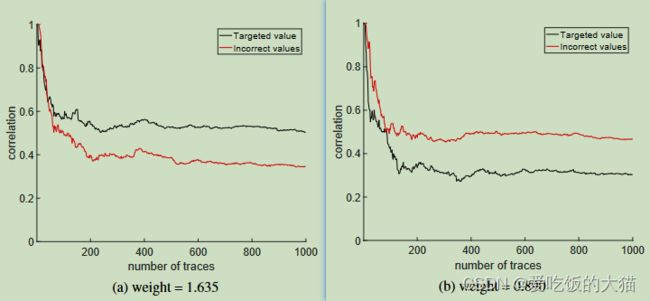
然后作者又给出了上面两幅图，代表的是在考虑简单情况下，即权重的尾数仅为7位，而不是上面的23位权重，在这种情况下作者采用上面的方法恢复出来的权重的相关系数的曲线，画了一条正确的和一条其他的错误的权重的相关曲线，从左图可以看到的是，恢复的被认为是正确的权重的相关系数大，这理所当然

但是，右图中，恢复的被认为正确的权重的相关性反而更低，无法从上面作者的理论中：相关函数更大的权重可以被视作是正确权重的估计

但是，作者接下把weight=0.890的恢复数据展示了出来，称恢复出来的权重实际上为0.890625，显然这个权重和0.890相差无几，但是他这样的搞的话，上面那两个图又能说明什么呢，在这个作者的话术中，意思是上图的这个Targeted value是真实权重，那他这个图又代表什么含义？

后来我又仔细看了看，这个段话就是上面这两张图对应的的名称，作者写的显然是黑线就是预测正确的权重对应的相关函数，红线就是其他的、预测错误的权重对应的相关曲线，但是图b是一种特殊情况，特殊在于，错误的预测拥有更高的相关系数，但是这个错误的权重为0.986025，实际上与真实值0.980也相差无几，显然是作者正文中对于这个图的解释给我给整懵了

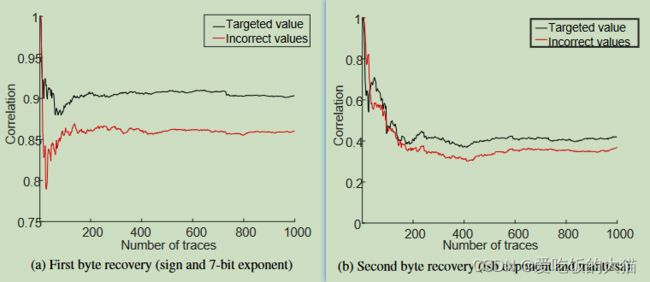
上图为作者展示的恢复的一个只有两位的权重，Targeted(正确)和其他的权重的相关系数之间从差距还是比较明显的，作者意为不管低精度还是高精度，都能通过此方法恢复权重

3.5、Reverse engineering the number of neurons and layers

每一层的单元数可以从上图直观看出，但是层与层之间的分割则不是那么容易看出，因此作者提出用CPA的方法，计算相关函数，来判断两个层的边界

CPA的方法如下：

1. 对于第n个节点，计算其在输入x=[x1,…,xm]下恢复的权重w1
2. 对于前n-1个节点，计算其在输入x=[x1,…,xm]下恢复的权重w2
3. 比较两个权重计算过程中出现的最大的相关系数，如果两者接近，则两个节点属于同一层，否则，两个节点分属不同层

3.6、Recovery of the full connected nework layer

4、Experiments with ARM Cortex-M3

上面的理论分析都是基于一个8位的AVR平台进行的，作者另一个32位的ARM平台上进行了一个验证实验，分为3步:确定激活函数、确定模型权重、确定模型结构

• 确定激活函数

上面这幅图是作者理论分析时，在8位的AVR平台上测量的不同激活函数的时延情况，而下图则为本节中32位的ARM平台上测量的不同激活函数的时延情况：

可以看到，除了relu的两次结果一样之外，另外两个激活函数可以说是天差地别，原本在8围殴的AVR平台时sigmoid的最大值和均值都更大，但是实际测量的时候，却变成了Tanh的最大值和均值更大，简单来说就是，sigmoid和tanh两个激活函数的时延特性发生了翻转，作者给出的说明如下：

个人理解为：每一个平台上神经网络的时延，噪声情况都不一样，一个平台测出来的标准不能通用到其他平台上，因此作者在这个32位的ARM上也测了不同的激活函数带来的时延，以此来做新的模式匹配，以确定用的是哪个激活函数

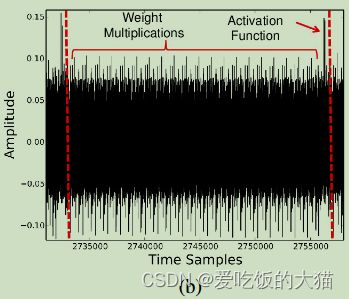
然后作者给出了下面这张图，说是这个是某一个节点的sigmoid激活函数的行为，并称红实线处代表的是乘法运算的开始，可能这是作者从一整个EM信息种截取的一小段，红线左边是上一个节点的激活函数，红线右边是这个节点的乘法操作和激活函数，但是这个不标注出两个节点来，令人看的有点不清楚，不知道这个节点的乘法操作和激活函数具体是哪儿到哪儿

• 确定权重

为了应对测量的不准确性，作者将对权重的恢复定在了做完乘法操作得出结果后，将结果m更新至寄存器的过程中，某一权重的相关曲线如下

• 确定层数与层大小

作者根据前文中的方法区分不同的层，然后以肉眼区分同一层里面的不同单元

4.1、Reverse Engineering MLP

被测MLP的结构拥有4个隐藏层，每个隐藏层的大小分别为（50，30，20，50）

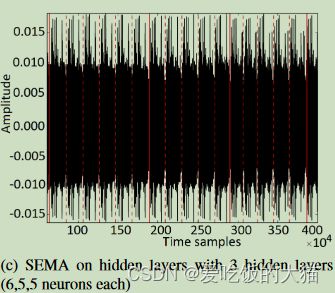
下图是作者测量的MLP的EM信号：

可以看到的是，这密密麻麻的，但是在250w-400w之间是有一段缺口的，作者认为这一段便是模型的运行，然后截取了其中的一小段，大概3w个点，估计是作者数过了，说这是第三层的一个单元：

被测MLP的精度为60.9%，作者recover的MLP的精度为60.87%，然后作者提出了实验中出现的几个问题：

• 为了提高SNR，作者选择了多次采用取平均，但是取平均意味着大量数据，处理比较耗费时间，因此作者比较推荐使用示波器的自动多次测量，自动取平均的功能
• 当测量跨度太大而超过测量范围时，可以选择只测量两个相邻的层，以保持层的连续性，以及方便确定层的边界
• 需要同步每一次测量的trace

然后又测了一个MLP with 4个隐藏层（200，200，200，200），使用minist数据集进行测试，原始网络的精度为98.16%，recover的网络的精度为98.15%

4.2、Reverse Engineering CNN

被测的CNN的结构为3层卷积+3层最大池化+1层全连接，输入为32*32，输出为10个类别，使用的是8位的定点数

5、Mitigation

• 由于recover需要顺序的执行每一个乘法，所以可以通过随机计算一层里面的乘法操作来抵御此类测通道攻击

• 采用掩码来计算乘法操作
  

• 激活函数可以选择为时延都差不多的那些，防止被攻击者区分出来用了什么激活函数