[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks
论文原文:Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks | IEEE Journals & Magazine | IEEE Xplore
目录
1. 省流版
1.1. 心得
1.2. 论文框架图
2. 论文逐段精读
2.1. Abstract
2.2. Introduction
2.3. Related Work
2.3.1. Handcrafted Methods
2.3.2. GNN-Based Methods
2.4. Proposed Method
2.4.1. Local ROI-GNN
2.4.2. Global Subject-GNN
2.5. Materials and Classification Evaluation
2.5.1. Materials
2.5.2. Experimental Setting
2.6. Experimental Results
2.6.1. Classification Results on Different Datasets
2.6.2. Ablation Studies
2.6.3. Biomarker Detection
2.6.4. Discussion
2.7. Conclusion
3. Reference List
1. 省流版
1.1. 心得
(1)他消融实验居然替换别的模块消,好勇啊...不过这样感觉确实能说明它们模型挺牛掰hh
1.2. 论文框架图
2. 论文逐段精读
2.1. Abstract
①The authors emphasize the current fMRI classification models ignores non-imaging information and relationships between subjects or misidentify brain regions or biomarkers
②Then, they put forward a local-to-global graph neural network (LG-GNN) to solve these problems
2.2. Introduction
①The diagnosis of Autism Spectrum Disorder (ASD) and Alzheimer’s disease (AD) is limited and inexperienced
②A Harvard-Oxford atlas maps of brain
③Graph neural networks (GNNs) has been found suitable for brain network analysis
④There are two types of GNN: regional brain graph and subject graph. The first one is good at local brain regions and biomarkers analysis, but ignores age, gender or relationships between subjects. And subject graph is just the opposite
⑤Therefore, they combine two methods to combine their advantages. They first adopt local, then expand to global
⑥Contribution: a) end to end LG-GNN, b) a pooling strategy based on an attention mechanism, c) excellent performances in 2 datasets
etiological adj.病因;病原学的,病原学的
aberrant adj.异常的;反常的;违反常规的
2.3. Related Work
2.3.1. Handcrafted Methods
①Functional connection construction by calculating Pearson correlation coefficient or "extracting weighted local clustering coefficients from the brain connectivity network from rs-fMRI, and then employed multiple-kernel based-SVM algorithm for the subsequent MCI classification"
②"Using SVM to classify AD from normal control (NC) after PCA and Student’s t-test for dimension reduction based on shape and diffusion tensor imaging"
③Also, different ROI may impact on the prediction accuracy
2.3.2. GNN-Based Methods
(1)GNNs Based on Regional Brain Graphs
Models such as DS-GCNs, s-GCN, MVS-GCN and mutual multi-scale triplet GCN etc. adopt regional graphs
(2)GNNs Based on Subject Graphs
Models such as GCN, InceptionGCN and SAC-GCN etc. adopt subject graphs
2.4. Proposed Method
①Framework of LG-GNN:
2.4.1. Local ROI-GNN
(1)Regional Brain Graph Construction
Approach of graph ![]() construction, each graph is represented as
construction, each graph is represented as ![]() :
:
(2)Local ROI-GNN Model
①Local ROI-GNN framework:
it consists of three graph convolution (GC) layers and the Self-Attention Based Pooling (SABP) module
②The activation in GC layer:
where ![]() denotes the degree matrix of
denotes the degree matrix of ![]() ;
;
![]() represents trainable weight matrix in the
represents trainable weight matrix in the ![]() -th layer;
-th layer;
③Receptive field: one hop neighborhoods
④For getting two-hops information, they adopt 2 GC layers. Then they get ![]()
(3)Self-Attention Based Pooling
①Pooling is essential in preserving and highlighting important ROI
②Transform ![]() to attention score
to attention score ![]() by
by ![]() .
.
③Through ![]() , selecting the top-
, selecting the top-![]() nodes
nodes ![]()
④Then, follows a pooling layer (?) ![]() and a
and a ![]()
⑤Finally, obtain new adjacency matrix ![]()
⑥They designed a loss to separate ROI weights
![]()
where ![]() is randomly shuffled
is randomly shuffled ![]() in channels (我也不知道有什么用啊).
in channels (我也不知道有什么用啊).
⑦The output will be:
![]()
where ![]()
⑧我很想知道为什么作者说SABP可以考虑到拓扑关系啊,脑图不是无向图吗而且也不会有什么先后关系吧??
2.4.2. Global Subject-GNN
(1)Subject Graph Construction
①There are ![]() subjects, i.e.
subjects, i.e. ![]() vector
vector ![]()
②![]() is the adjacency matrix of
is the adjacency matrix of ![]() , where
, where ![]() is a binarized connectivity matrix of the combination of non-image information and information (with values greater than 0.4 becoming 1, and values less than 0.4 becoming 0)
is a binarized connectivity matrix of the combination of non-image information and information (with values greater than 0.4 becoming 1, and values less than 0.4 becoming 0)
③There is a similarity matrix ![]() , where
, where ![]() denotes the correlation distance,
denotes the correlation distance, ![]() is mean of
is mean of ![]()
④Node similarity metric ![]() is constructed by non-image information
is constructed by non-image information
⑤![]()
⑥Weight matrix ![]() , where
, where ![]() and
and ![]() are both non-image information, Sim reperesents the cosine similarity, the 2 MLP layers share the same weights
are both non-image information, Sim reperesents the cosine similarity, the 2 MLP layers share the same weights
(2)Global Subject-GNN Model
①A multi-scaled residual model was proposed as:
②Cheb conv is:
![]()
where ![]() looks like the eigenvalues of each node;
looks like the eigenvalues of each node;
![]() denotes a filter;
denotes a filter;
![]() denotes parameter;
denotes parameter;
![]() denotes convolution operator;
denotes convolution operator;
![]() is come from Laplace matrix
is come from Laplace matrix ![]() ;
;
③To save the calculating time, they approximate the above function to:
![]()
where ![]() is a rescaled Laplace graph,
is a rescaled Laplace graph, ![]() denotes a learnable parameter
denotes a learnable parameter
④The recursion might be ![]() ,
, ![]() ,
, ![]()
⑤Given the ![]() , there is
, there is ![]()
⑥The final embedding ![]() ,
,
![]() denotes random initialized learnable weight;
denotes random initialized learnable weight;
(3)Total Training Loss
①They adopt cross entropy loss as the global loss:
![]()
②They combine local ![]() and global
and global ![]() to get total loss:
to get total loss:
![]()
where the hyper parameter ![]() is set as 0.1
is set as 0.1
2.5. Materials and Classification Evaluation
2.5.1. Materials
They choose two datasets ABIDE, ADNI in 4 tasks:
(1)ABIDE Dataset
①They only select 871 samples from 1112 subjects with 403 ASD and 468 NC in 20 different sites.
②Preprocess pipeline: C-PAC
③Space: normalized in MNI152 space
(2)ADNI Dataset (NC and MCI)
①Preprocess: standard protocol
②Excluding significant artifacts or head movements beyond 2mm amplitude
③They choose 134 subjects with 96 MCI and 40 AD (不是,我有点不太理解这句话,40+96也不等于134吧?)
(3)ANDI Dataset (pMCI and sMCI)
①pMCI patients: deteriorating within 36 months; sMCI patients: do not deteriorate
②Atlas: Harvard-Oxford
③They choose 41 pMCI and 80 sMCI subjects excluding NaN data
④Preprocessing: standard procedures on GRETNA toolkit
2.5.2. Experimental Setting
①Optimizer: Adam
(1)Parameters of ABIDE
①Dropout rate: 0.3
②Learning rate: 0.01
③Maximum epochs: 400
④Non-image data: acquisition site, gender
(2)Parameters of ANDI
①Dropout rate:0.3
②Learning rate: 0.01
③Maximum epochs: 300
④Non-image data: gender and age
②Chebyshev polynomial order K: 3
③Cross-validation: 10-fold, 9 for training and 1 for test
④Evaluation metrics: classification accuracy (Acc), area under the curve (AUC), sensitivity (Sen) and F1-score
⑤这里的ROI Dimension是什么东西?为什么是2000,2140之类的?Non-imaging dimension denotes (number of subjects, binary classification)
2.6. Experimental Results
2.6.1. Classification Results on Different Datasets
(1)Classification Results on ABIDE
①Comparison with handcrafted methods: Ridge Classifier, SVM, Random Forest classifier
②Comparison with GNN-based methods: GCN, GAT, BrainGNN, MVS-GCN, PopulationGNN, InceptionGCN, EV-GCN, Hi-GCN
③Comparison with deep neural network (DNN) based methods
④The classification results (NI denotes whether adopting non-image data or not):
(2)Classification Results on ADNI (NC and MCI)
①Models in ANDI mostly outperform those in ABIDE in that data in ABIDE is highly heterogeneous (they come from different acquisition site)
②The classification results (NC and AD):
③The classification results on NC and MCI:
④The classification results on pMCI and sMCI:
2.6.2. Ablation Studies
(1)Ablation Study for Local ROI-GNN
①They compared local ROI-GNN with GAT, GIN, GraphSAGE, ChebNet, GCN, which means adopting these SOTA models in their model (replace local ROI-GNN)
②They found SABP module significantly enhances the performance. Specifically, they reckon appropriate pooling is vital. Excessive pooling may retain a lot of noise, but too small pooling may cause the topology information of the graph to be compressed. Thus, they choose 0.9 pooling rate.
③Replaced classification results:
④Different pooling rate in SABP module:
(2)Ablation Study for Global Subject-GNN
①They replaced subject-GNN by GATConv, GINConv, GraphSAGEConv, GCNConv
②Replaced classification results:
③To evaluate the effectiveness of AWAB module, they tried with or without (adopting output of the last Cheb block as the final output) AWAB in the table above
2.6.3. Biomarker Detection
①They obtain weights of ROI through SABP module, and select top 10 ROI as biomarker
②Mutual information loss ![]() is what they distinguish ROIs with putting important ROI weights to 1, other to 0
is what they distinguish ROIs with putting important ROI weights to 1, other to 0
③The top 10 ROIs with the greatest impact on autism and Alzheimer's disease:
2.6.4. Discussion
①Acquisition site significantly affects the results, and gender impacts on classification as well in ABIDE dataset:
②Gender impacts more than age in ANDI:
③Other non-imaging data can also be used, such as IQ and genetic informatio(???你可以再写离谱一点吗我真的,这)
quotient n.商(除法所得的结果)
2.7. Conclusion
Their model LG-GNN with local and global modules achieve excellent performance
3. Reference List
Zhang, H. et al. (2022) 'Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks', IEEE, vol. 42 (2), pp. 444-455. doi: 10.1109/TMI.2022.3219260
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第1张图片](http://img.e-com-net.com/image/info8/d59b1a3b007748d1bd15ad28f7a0da44.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第2张图片](http://img.e-com-net.com/image/info8/08b54fb349b04725a6d58c74ae9a84a0.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第3张图片](http://img.e-com-net.com/image/info8/a28af0ff0e464a409967d4c06a86e671.jpg)
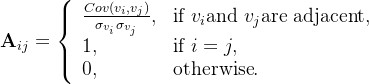
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第4张图片](http://img.e-com-net.com/image/info8/be3ebf7e32e44394b9505f5046f710ee.jpg)
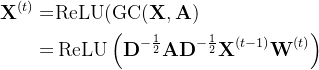
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第5张图片](http://img.e-com-net.com/image/info8/7ee442e78bcd4651b5124fa106a630aa.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第6张图片](http://img.e-com-net.com/image/info8/cf4259d0b00a446fa56951c37c219c5b.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第7张图片](http://img.e-com-net.com/image/info8/e637b49664f6443890147e2e682d009b.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第8张图片](http://img.e-com-net.com/image/info8/91a19e731f3a481c842993932eb32c0b.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第9张图片](http://img.e-com-net.com/image/info8/dd022449822f4e64bda60350fe3ac6e3.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第10张图片](http://img.e-com-net.com/image/info8/727bced48dd54a4fb7110b46ff8911a6.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第11张图片](http://img.e-com-net.com/image/info8/e71b679cf102483787381d9c41f2a69b.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第12张图片](http://img.e-com-net.com/image/info8/943d711b896448f0afc29d67f31c27d6.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第13张图片](http://img.e-com-net.com/image/info8/9e1ee38adc224a4d99493d59e2c01476.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第14张图片](http://img.e-com-net.com/image/info8/6c8d63915b314cec898210c518408727.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第15张图片](http://img.e-com-net.com/image/info8/06329404bd124264b9660325e7689330.jpg)
![[论文精读]Classification of Brain Disorders in rs-fMRI via Local-to-Global Graph Neural Networks_第16张图片](http://img.e-com-net.com/image/info8/539157a17a794415b05a7407b1bc88a3.jpg)