【刷题笔记】匹配字符串||KMP||动图解析||符合思维方式
找出字符串中第一个匹配项的下标
1 题目描述
https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
2 思路
其实说白了,这道题的意义就是为了让我们理解KMP算法。
网上很多讲解一上来就解释next数组怎么构建的,如何计算前缀等。但是我认为最重要的还是先明白KMP算法在做什么。
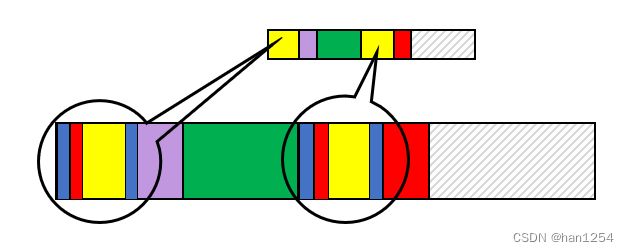
如下图,图中有上下两个字符串,上串为haystack,下串为needle。
右移:
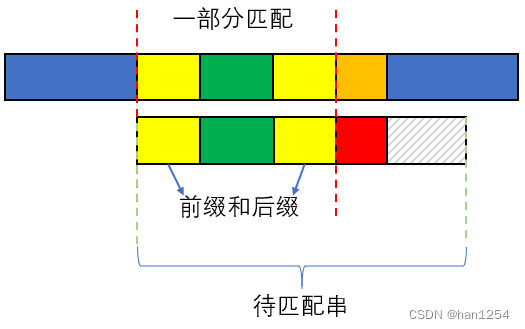
提示:为了让大家清晰地看懂我要说什么,这里我先规定几个词的含义:
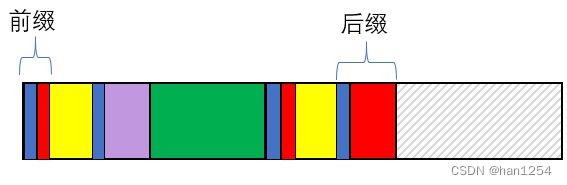
前缀和后缀:指的是在needle的子串(我们设置为part_needle=needle[:n])中,一个从头开始的字符子串a和一个与其相同的但是末尾是part_needle的末尾的字符子串b
即:
a=[part_needle[0], ..., part_needle[1], ..., part_needle[prefix_len-1]
其实本质上也是a=[needle[0], ..., needle[1], ..., needle[prefix_len-1]
b=[part_needle[-prefix_len]], part_needle[-(prefix_len - 1), ..., part_needle[-1],:
a==b
prefix_len就是前缀和后缀的长度,而且是子串part_needle中满足条件的最大值。
如果嫌麻烦可以看看上面的第一张图就一目了然了。
我们的目标是,当遇到不匹配的时候,能够让needle尽可能地右移动,而不是每次只移动一个位置。为什么?
我们先看一个动图:
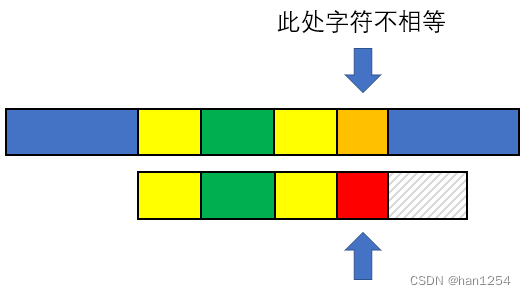
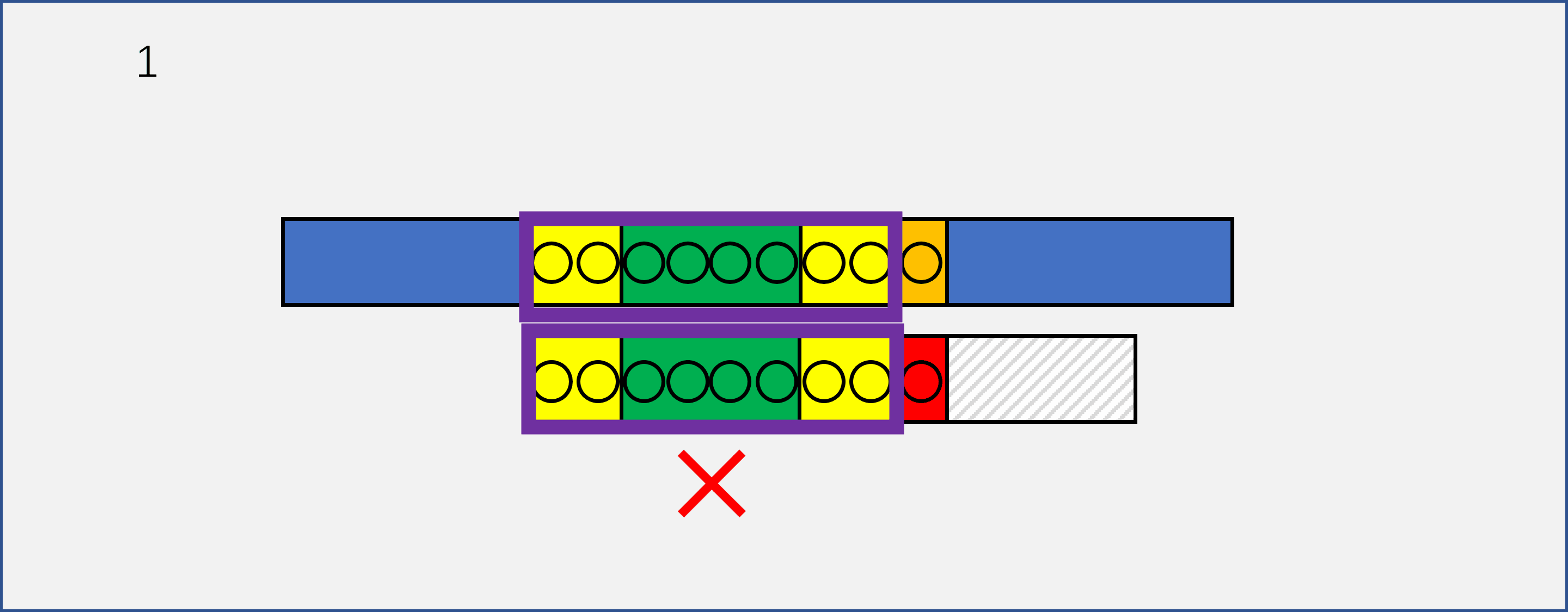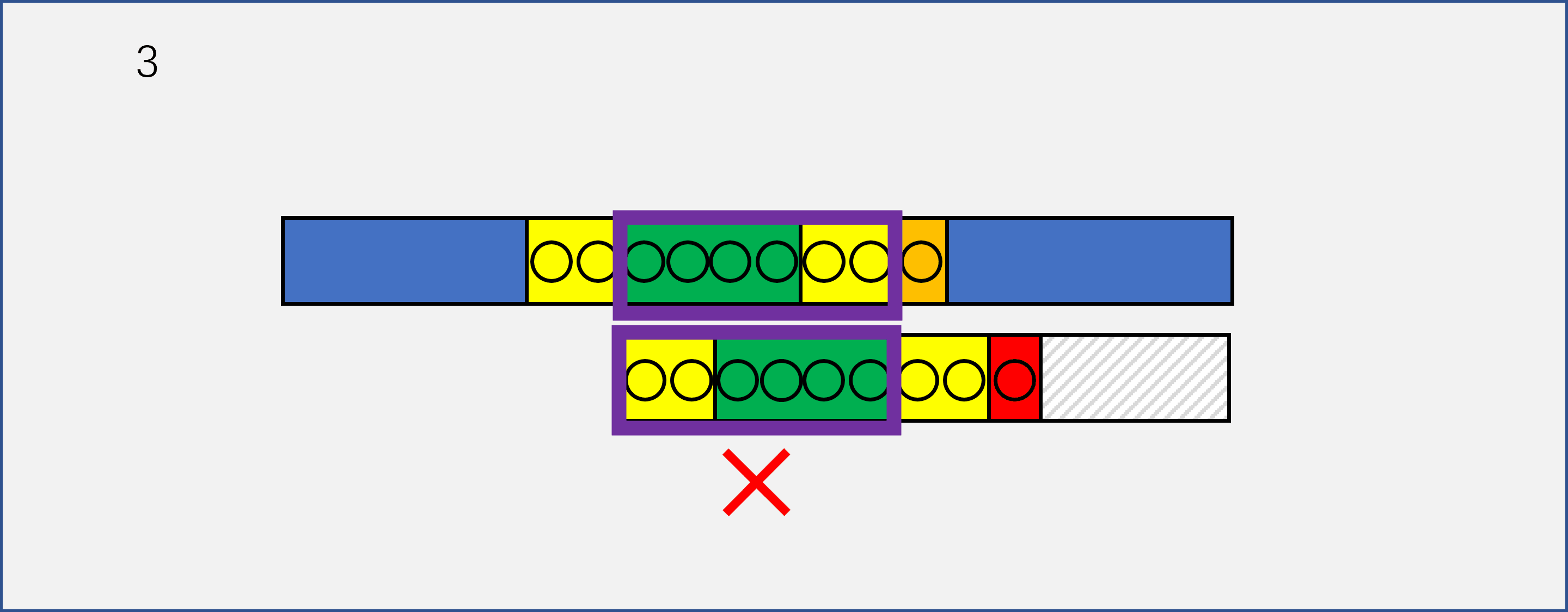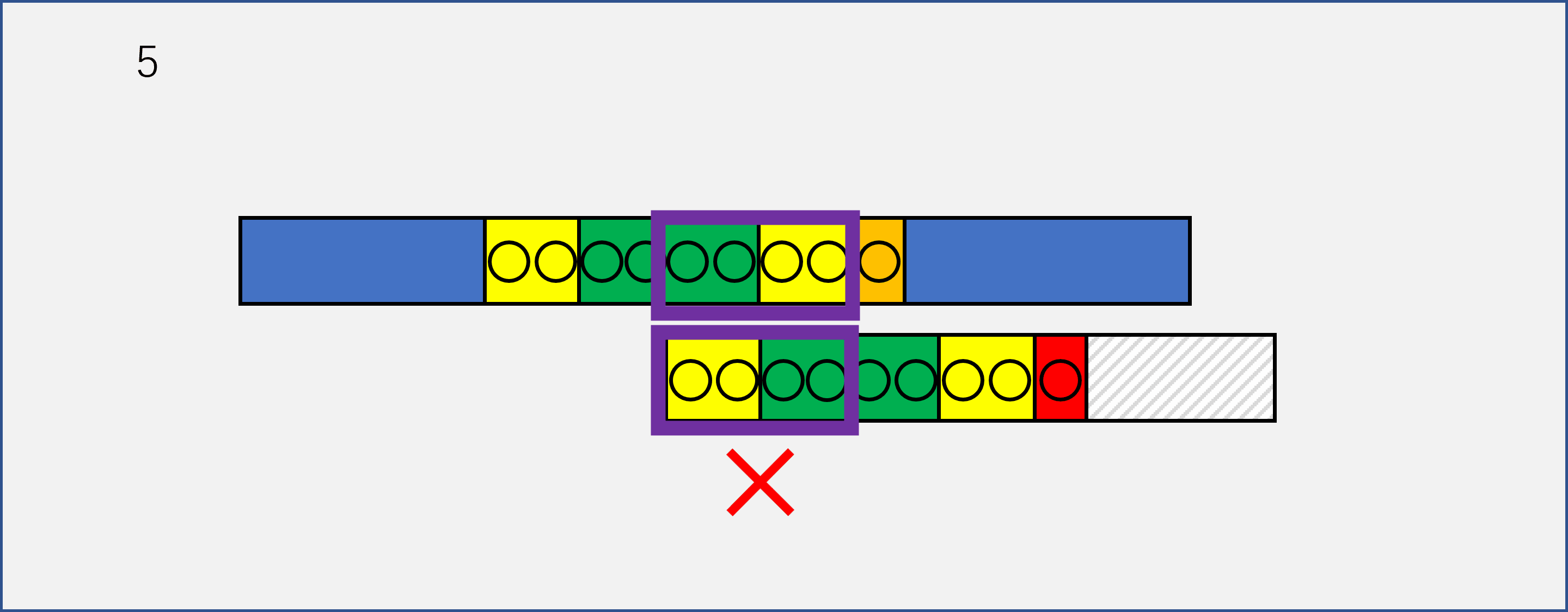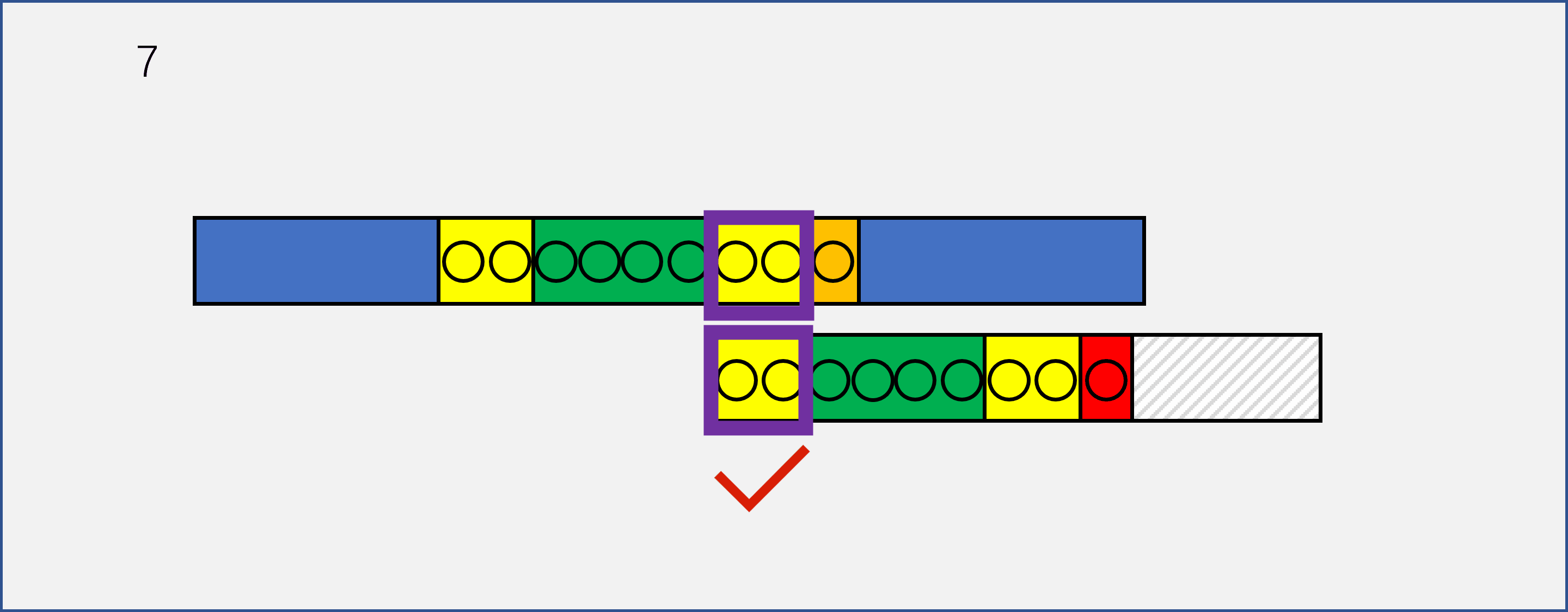
我们这里将一开始的图进行了细化,可以看到,needle和haystack已经有8个字符完成了匹配(黄色和绿色字符),在第九个字符的时候,haystack是橘色,needle是红色,不匹配。我们可以看到,正常情况下的第一个想法是将needle后移一位,重新开始匹配。
此时,红色字符之前的八个字符已经构成了一个needle的子串part_needle=needle[:8]。假设我们已经找到了这个子串中最长的前缀和后缀(黄色部分),那么在前六步移动的时候,请仔细看紫色框里的字符串,这些字符串是不可能相等的,因为我们知道在前八个字符中,只有前两个字符构成的串和倒数后两个字符构成的串相等,那么我们可以直接跳过前六步,到达第七步。
注意,上面这段话的描述是KMP思想的关键,只有看懂了我上面说的什么,你才能知道KMP到底在干什么。请结合动图再看一遍,我希望我能够把我领悟到的东西让你也感受到。
那么我们现在的目标就是找出,needle的每个子串(注意都是从0号索引开始的子串)的前缀和后缀。比如needle为leetcode,那么子串分别为:
l 第0个子串
le 第1个子串
lee 第2个子串
leet 第3个子串
leetc
leetco
leetcod
2.1 找到前缀长度
知道了子串是什么之后,我们要想找前缀和后缀,本质上就是在找前缀和后缀的长度。
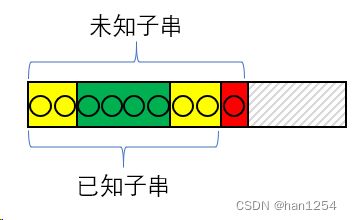
当我们到达一个未知子串的时候,该怎么找到未知子串中的前缀和后缀呢?
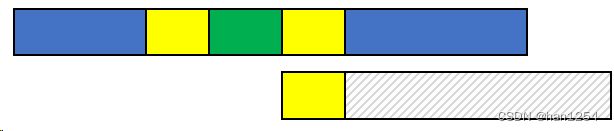
但是此时我已经有了前面所有子串的前缀和后缀,如果当前的字符(红色)和前缀后面的字符相等,如下图所示,
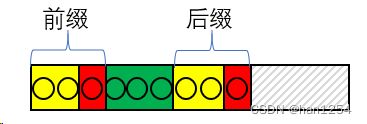
那么便可以确定当前的前缀和后缀了。
可是如果不等呢?是不是就说明当前未知子串没有前后缀?非也。我们换一种表示方式,不用圆圈表示字符了,只用颜色表示字符。
我们发现,虽然紫色和红色不相等,但是在黄色区域中,放大来看其实内有乾坤(黄色区域其实只是表示一个字符串),黄色区域也有前缀和后缀(蓝色部分),第一个黄色区域和第二个黄色区域具有量子纠缠的神奇性质,因为它们相等,所以第一个黄色区域的特征,第二个黄色区域也全都有。黄色区域的前缀蓝色,下一个字符是红色,正好跟我们的未知子串的最后一个字符一样是红色。
(不要考虑宽度,宽度在本小节的语境下没有意义)
这样我们知道了,如果我们的未知子串的最后一个字符和已知的上一个子串的前缀的后一个字符不相等,那么我们可以让未知字符的子串继续跟前缀的前缀的后一个字符去比较,一直迭代下去。直到找到相等字符或者某个前缀内部已经没有前缀了。
Wait,上面的叙述,好像就是动态规划吧。当前字符串的前后缀长度和上一个字符串有关。
我们设这个记录长度的数组为:
int[] prefix_len_dps = new int[needle.length()];
prefix_len_dps[0] = 0;
比如prefix_len_dps[2]就是记录的前三个字符构成的字符串的前后缀长度。
for (int i = 1; i < needle.length(); i++) {
int prefix_len = prefix_len_dps[i - 1]; // 前一个子串的前后缀长度
while (needle.charAt(prefix_len) != needle.charAt(i) && prefix_len > 0)
// 首先我们要理解一点,长度可以用作下标,
// needle.charAt(prefix_len)其实就是第i-1个子串前缀的后面一个字符
// 如果needle.charAt(prefix_len) != needle.charAt(i),说明我们需要找前缀的前缀
// 我们说过,prefix_len是第i-1个子串前缀的后面一个字符的位置,那么
// prefix_len-1就是第i-1个子串的末尾的位置,
// prefix_len_dps[prefix_len - 1]表示的就是第i-1个子串的前缀长度,即前缀的前缀的长度
// 如果prefix_len==0,这说明第i-1个子串没有前缀,那么我们直接跳出循环,让第i个子串
// 的第一个字符跟最后一个字符相比较
prefix_len = prefix_len_dps[prefix_len - 1];
if (needle.charAt(prefix_len) == needle.charAt(i)) prefix_len++;
prefix_len_dps[i] = prefix_len;
}
2.2 找到匹配下标
int j = 0;
for (int i = 0; i < haystack.length(); i++) {
while (haystack.charAt(i) != needle.charAt(j) && j > 0) {
j = prefix_len_dps[j - 1] // 循环,找到第一个可以匹配的j
// 其实这里的逻辑跟前面是一样的,我们期待接下来的i和j位置上的
// 字符可以相等,如果不相等,就继续找其前缀的后一个位置,还不等,那就找前缀的前缀。。。
// 一直到j==0,没有前缀了,跳出,然后直接比较
// needle的第一个字符和haystack在i位置上的字符
}
if (haystack.charAt(i) == needle.charAt(j)) j++;
if (j == needle.length()) return i - needle.length() + 1;
}
3 代码
class Solution {
public int strStr(String haystack, String needle) {
int[] prefix_len_dps = new int[needle.length()];
prefix_len_dps[0] = 0;
for (int i = 1; i < needle.length(); i++) {
int prefix_len = prefix_len_dps[i - 1];
while (needle.charAt(prefix_len) != needle.charAt(i) && prefix_len > 0)
prefix_len = prefix_len_dps[prefix_len - 1];
if (needle.charAt(prefix_len) == needle.charAt(i)) prefix_len++;
prefix_len_dps[i] = prefix_len;
}
int j = 0;
for (int i = 0; i < haystack.length(); i++) {
while (haystack.charAt(i) != needle.charAt(j) && j > 0)
j = prefix_len_dps[j - 1];
if (haystack.charAt(i) == needle.charAt(j)) j++;
if (j == needle.length()) {
return i - needle.length() + 1;
}
}
return -1;
}
}