基于隐马尔可夫模型的一种流水印
文章信息
论文题目:An Invisible Flow Watermarking for Traffic Tracking: A Hidden Markov Model Approach
期刊(会议):ICC 2019 - 2019 IEEE International Conference on Communications (ICC)
时间:2019
级别:CCF C
文章链接:https://sci-hub.yt/10.1109/icc.2019.8761135
概述
本文提出了基于隐马尔可夫的流水印技术(Hidden Markov State-based Flow Watermarking, HMSFW),其使用历史流量特征作为干扰当前流量的衡量标准,从而使嵌入水印前后的流量特征非常相似。为了基于历史流量特征向当前流量嵌入水印,本文将流量的IPTs值范围分成相等的部分作为隐马尔可夫状态,并引入状态转移概率均值(STPM)作为水印载体。为了处理STPM作为水印载体的随机性,本文将时间间隔分为预测部分和水印部分,它们的STPM分布分别映射为离散均匀分布。
相关工作
流水印技术可以分为三类:
- 基于流速的流水印:DSSS-FW技术,但被均方自相关技术降低了实用性;
- 基于包大小的流水印
- 基于时间间隔的流水印
- 基于数据包计数的技术:调整数据包间隔时间以操纵特定间隔内的数据包数量,以嵌入水印;
- 基于数据包间隔时间的技术
- 基于间隔重心的技术
- 基于丢包的技术
本文方案
HMSFW的基本思想是将流f的一系列包间间隔(IPTs)描述为隐马尔可夫状态序列。然后,HMSFW根据预先存储的历史流(与流f相同)和利用机器学习技术从历史流中学习到的状态转移概率矩阵 Φ \Phi Φ,调整隐马尔可夫状态序列。
隐马尔可夫状态和STPM的设计
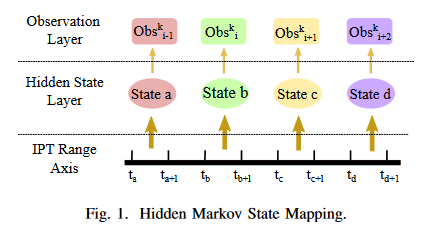
由于数据包的IPT不会被改变,所以我们将IPT用于状态的设计,于是可以用隐马尔可夫模型的隐藏状态来描述数据包的IPT。设 Σ \Sigma Σ代表网络流的所有可能的IPT集合。 Σ \Sigma Σ中IPT值的完整范围被等分为 V V V个相等长度的子范围 r v s u b r_{v}^{sub} rvsub,其中下标v代表第v个子范围。每个 r v s u b r_{v}^{sub} rvsub代表一个隐马尔可夫状态 S v S_{v} Sv,例如, S v ⇔ [ τ s t a r t v , τ e n d v ) , τ e n d v − τ s t a r t v = l S_{v}\Leftrightarrow [\tau_{start}^{v},\tau_{end}^{v} ),\tau_{end}^{v}-\tau_{start}^{v}=l Sv⇔[τstartv,τendv),τendv−τstartv=l。让我们用 O b s i k Obs_{i}^{k} Obsik来代表 I P T i k IPT_{i}^{k} IPTik的值,其中k是第k个选择的时间段,i是该时间段内第i个观测。每个观测,即 O b s i k ∈ [ τ s t a r t k , τ e n d k ) Obs_{i}^{k}\in [\tau _{start}^{k}, \tau _{end}^{k}) Obsik∈[τstartk,τendk),与某个隐马尔可夫状态 S v S_{v} Sv相对应,其中 O b s i k ∈ S v Obs_{i}^{k}\in S_{v} Obsik∈Sv。接收到的流的观测序列 o b s k \mathbf{obs}_{k} obsk对应了一个隐马尔可夫状态序列 s t a t e k \mathbf{state}_{k} statek,即 { O b s i − 1 k , O b s i k , O b s i + 1 k , O b s i + 2 k } → { S a , S b , S c , S d } \{Obs_{i-1}^{k},Obs_{i}^{k},Obs_{i+1}^{k},Obs_{i+2}^{k}\}\to \{{S_{a},S_{b},S_{c},S_{d}}\} {Obsi−1k,Obsik,Obsi+1k,Obsi+2k}→{Sa,Sb,Sc,Sd},如图1所示。
设 P ( i − 1 , i ) k P_{(i-1,i)}^{k} P(i−1,i)k代表从 S a S_{a} Sa到 S b S_{b} Sb的隐马尔可夫状态转移概率。给定任何特定的状态转移概率序列 { P ( 1 , 2 ) , ⋯ , P ( N − 1 , N ) } \{P_{(1,2)},\cdots, P_{(N-1,N)}\} {P(1,2),⋯,P(N−1,N)}和转移概率范围P。当N足够大时, P ( i − 1 , i ) P_{(i-1,i)} P(i−1,i)在范围 [ 0 , P ) [0,P) [0,P)近似均匀分布。
在一段时间 T k ( k = 0 , ⋯ , K ) T_{k}(k=0,\cdots,K ) Tk(k=0,⋯,K)内,假定有 N + 2 > 0 N+2>0 N+2>0个数据包,从而对应了 N + 1 N+1 N+1个IPT。IPT是我们观测到的值,在隐马尔可夫模型中,观测值都是由隐藏状态确定的,从而对应了一个状态转移概率序列 { P ( 0 , 1 ) , ⋯ , P ( N − 1 , N ) } \{P_{(0,1)},\cdots, P_{(N-1,N)}\} {P(0,1),⋯,P(N−1,N)},于是就可以定义STPM为 E k = A v T r a n ( s t a t e k ) = 1 N ⋅ ∑ i = 1 N P ( i − 1 , i ) k E_{k}=AvTran(\mathbf{state}_{k})=\frac{1}{N} \cdot \sum_{i=1}^{N}P_{{(i-1,i)}}^{k} Ek=AvTran(statek)=N1⋅i=1∑NP(i−1,i)k
我们继续将这段时间 T k ⇔ [ t s t a r t k , t e n d k ) T_{k}\Leftrightarrow [t_{start}^{k},t_{end}^{k} ) Tk⇔[tstartk,tendk)分为两部分:预测部分和水印部分。这俩部分在时刻 t s p l i t t e r k t_{splitter}^{k} tsplitterk分隔为 [ t s t a r t k , t s p l i t t e r k ) [t_{start}^{k},t_{splitter}^{k} ) [tstartk,tsplitterk)和 [ t s p l i t t e r k , t e n d k ) [t_{splitter}^{k},t_{end}^{k} ) [tsplitterk,tendk)。预测部分用于预测水印部分的隐藏状态序列,并指示要由水印部分携带的水印。水印部分用于携带水印,其由预测部分的STPM确定,可通过调整其状态序列顺序来实现。
水印嵌入
预测部分和水印部分的观测值会形成各自的隐藏状态序列 p f l o w k pflow_{k} pflowk和 e f l o w k eflow_{k} eflowk。通过Baum-Welch算法我们可以学习到状态转移矩阵 Φ \Phi Φ。
为了嵌入水印,我们首先通过Viterbi算法获取预测部分的隐藏状态序列 p f l o w k pflow_{k} pflowk,然后基于状态转移概率矩阵 Φ \Phi Φ和前向算法预测水印部分最有可能的隐马尔可夫状态序列。
为了提高嵌入水印的隐形性,本文将STPM服从的混合高斯分布映射到离散均匀分布,这能够使任何状态序列在任何时间间隔内嵌入水印的概率相等。我们将 p f l o w k pflow_{k} pflowk的混合高斯分布分成等概率的H部分,也就是概率密度函数按面积等分,并按x轴增长的方向编号每一部分。每一部分都是离散均匀分布中的一个离散值,可以表示为 P h m ⇔ [ E h M I N P , E h M A X P ) P_{h}^{m}\Leftrightarrow [E_{h}^{MIN_{P}},E_{h}^{MAX_{P}}) Phm⇔[EhMINP,EhMAXP),其中h表示第h部分,m为第m个水印模式。然后,我们将 e f l o w k eflow_{k} eflowk也同样操作,可以表示为 W h m ⇔ [ E h M I N W , E h M A X W ) W_{h}^{m}\Leftrightarrow [E_{h}^{MIN_{W}},E_{h}^{MAX_{W}}) Whm⇔[EhMINW,EhMAXW)。
水印模式指的是从 p f l o w k pflow_{k} pflowk离散均匀分布的某一部分到 e f l o w k eflow_{k} eflowk离散均匀分布的映射规则,用符号 p m p_{m} pm表示。映射规则可以是顺序映射,即 P h m → W h m P_{h}^{m}\to W_{h}^{m} Phm→Whm,逆序映射,即 P h m → W H − h m P_{h}^{m}\to W_{H-h}^{m} Phm→WH−hm,错位映射,即 P h m → W h + o m P_{h}^{m}\to W_{h+o}^{m} Phm→Wh+om,或者随机映射,即 P h m → W R a n d ( ) % H m P_{h}^{m}\to W_{Rand()\%H}^{m} Phm→WRand()%Hm,其中 0 ≤ o ≤ H 0\le o\le H 0≤o≤H是一个偏移量, R a n d ( ) % H Rand()\%H Rand()%H是一个随机数。每个映射规则从0到M编号,并且使用哪个映射规则是由水印嵌入器和检测器进行预先协商的。水印 s i g h m sig_{h}^{m} sighm,指的是在映射规则 p m p_{m} pm下, e f l o w k eflow_{k} eflowk的STPM所属的离散均匀分布部分的编号。
嵌入水印的具体过程可以描述如下:
- 根据Viterbi算法获取预测部分的隐藏状态序列 p f l o w k pflow_{k} pflowk;
- 计算 p f l o w k pflow_{k} pflowk的STPM,这个STPM会落在上面划分的离散均匀分布的某一个小区间内 E i P ∈ [ E h M I N P , E h M A X P ) E_{i}^{P}\in [E_{h}^{MIN_{P}},E_{h}^{MAX_{P}}) EiP∈[EhMINP,EhMAXP),从而得到对应的编号。根据映射规则 p m p_{m} pm得到水印 s i g h m = M a p p i n g ( E i P , p h ) sig_{h}^{m}=Mapping(E_{i}^{P},p_{h}) sighm=Mapping(EiP,ph),也就是水印部分的STPM应该落在的小区间的编号;
- 根据 s i g h m sig_{h}^{m} sighm确定小区间的具体范围 [ E h M I N W , E h M A X W ) ⇔ W h m [E_{h}^{MIN_{W}},E_{h}^{MAX_{W}})\Leftrightarrow W_{h}^{m} [EhMINW,EhMAXW)⇔Whm;
- 调整 e f l o w k eflow_{k} eflowk,使得它的STPM落在这个区间内。
上面有提到利用前向算法和状态转移概率矩阵计算 e f l o w k eflow_{k} eflowk。在计算的过程中,我们同时也要算每种可能的状态序列的STPM,确保STPM是落在上述区间内的。然后再选择符合条件的序列中概率最大的序列 e x p k \mathbf{exp}_{k} expk。
有了状态序列,我们接下来需要根据该状态序列得到观测序列。当然,在状态所确定的IPT范围内随机选择是一种办法。但是本文引入了历史数据集 H i s t o r y History History,其中保存了之前出现的流的IPT值序列。首先搜索历史数据集,如果有符合 e x p k \mathbf{exp}_{k} expk的观测序列就可以直接使用;否则就根据 e x p k \mathbf{exp}_{k} expk一个个调整,每次都选择历史数据集中符合要求的中最大概率的。
为了提升鲁棒性,靠近区间边界的IPT值在网络传播过程中可能会产生偏差,从而跑到另一个状态区间里去了。所以IPT观测值需要和边界保持一个最小距离 ε \varepsilon ε,也就是 τ s t a r t α + ε < O b s i k ′ < τ e n d α − ε \tau _{start}^{\alpha } +\varepsilon < Obs_{i}^{k^{'} } <\tau _{end}^{\alpha}-\varepsilon τstartα+ε<Obsik′<τendα−ε。
水印检测
检测器放置在网络中的一个或多个我们可能希望检测标记流的地方。
为了检测水印,检测器捕获K个时间段,每个时间段内的流的长度为T。检测器分析并计算每个时间段内预测部分的STPM值 E k P ~ \tilde{E_{k}^{P} } EkP~。如果 E k P ~ ∈ [ E x M I N P , E x M A X P ) \tilde{E_{k}^{P} } \in [E_{x}^{MIN_{P}},E_{x}^{MAX_{P}}) EkP~∈[ExMINP,ExMAXP),我们就可以根据映射规则 p m p_{m} pm确定水印部分的STPM值应该落在区间 [ E y M I N W , E y M A X W ) [E_{y}^{MIN_{W}},E_{y}^{MAX_{W}}) [EyMINW,EyMAXW)内。然后计算水印部分的STPM值 E k W ~ \tilde{E_{k}^{W} } EkW~,如果 E k W ~ \tilde{E_{k}^{W} } EkW~确实落在区间 [ E y M I N W , E y M A X W ) [E_{y}^{MIN_{W}},E_{y}^{MAX_{W}}) [EyMINW,EyMAXW)内,就检测出了水印。
为了消除漏检或误检,采用传统的概率阈值方法来进一步提高水印检测效果。假设在流f中嵌入了总共 X f X_{f} Xf个水印,检测器正确检测了 Y f Y_{f} Yf个,那么 P r f = Y f / X f Pr_{f}=Y_{f}/X_{f} Prf=Yf/Xf被称为水印检出率。我们设置一个阈值 ρ \rho ρ来确定一个流是否被嵌入了水印。如果 P r f ≥ ρ Pr_{f}\ge \rho Prf≥ρ,我们认为该流被嵌有水印;否则,它是一个未标记的流。
实验评估
本文在2018年9月7日至8日和10月1日至5日通过Python模拟了HMSFW水印系统; 这些数据是从WIDE MAWI存档中随机选择的。在WIDE数据集中,从跟踪中选择了安全外壳(SSH)流进行实验,因为SSH经常与交互式跳板一起使用,其行为类似于绕过审查的系统。根据统计数据,用于实验的数据集包含404个SSH流。在实验中,我们选择了404个SSH流中的64个来嵌入829个水印。
True Positive(TP):实际嵌入了水印,检测也认为嵌入了水印
False Negative(FN):实际嵌入了水印,但检测认为没有水印
False Positive(FP):没有嵌入水印,但检测认为嵌入水印
True Negative(TN):没有嵌入水印,检测也认为没有嵌入水印
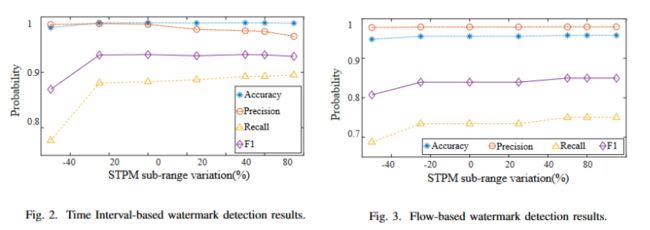
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy=\frac{TP+TN}{TP+TN+FP+FN} Accuracy=TP+TN+FP+FNTP+TN
F 1 = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F_{1}=\frac{2\times Precision\times Recall}{Precision+Recall} F1=Precision+Recall2×Precision×Recall
图4和图5分别是在嵌入水印前后的流量观测的统计分布图,其中x轴代表IPT,y轴表示IPT的发生概率。图4和5中的小图是在x轴范围为[100, 300)上的放大。
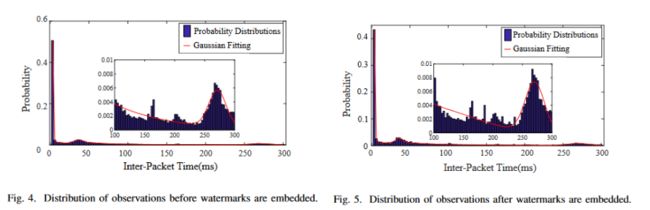
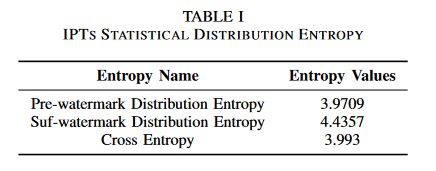
表1显示了嵌入水印前后的IPTs分布熵以及两个分布的交叉熵。
总结
本文提出了使用隐马尔可夫模型嵌入水印的HMFSW方法,可以提高水印的鲁棒性和隐形性。 HMFSW采用STPM作为新的水印载体,并通过使用STPM分布映射保持信号的等概率性。水印根据历史流量信息的直接特征或统计特征进行嵌入。实验结果表明,所提出的HMFSW对具有良好隐形性的水印具有较高的检测率。