查找的知识点

目录

思维导图：

一.基本概念：

二、查找方式：

a.顺序查找

b.二分查找

c.二叉排序树

d.哈希表

---

前言：

        查找：就是在数据集合中寻找满足某种条件的数据对象。

思维导图：

一.基本概念：

查找：就是在数据集合中寻找满足某种条件的数据对象。
关键码：在每个对象中有若干属性，其中有一个属性，其值可唯一地标识这个对象，称为关键码。
静态搜索：搜索结构在插入和删除等操作的前后不发生改变。
动态搜索：为保持高的搜索效率，搜索结构在执行插入和删除等操作的前后将自动进行调整，结构可能发生变化。
静态：有序查找、折半查找
动态：非线性-树

ASL(平均查找长度):衡量查找算法的好坏
ASL=∑(i=1->n)PiCi
Pi为查找概率    Ci为查找次数

二、查找方式：

注：下面代码只给算法代码，源码可在GitHub搜索Lookdrama中的Loodrama-s-daily-firy下查询

a.顺序查找

操作过程：从表中的第一个（或最后一个）记录开始，逐个进行记录的关键字和给定值比较，若某个记录的关键字和给定值相等，则查找成功，找到所查索引；如果知道最后一个（或第一个）记录，其关键字和给定值比较都不等时，则表中没有所查的记录，查找不成功。

平均查找长度：(n+1)/2

时间复杂度：O(n)

代码：

int search(List* list,int key)
{
    for(int i=0;inum;i++)
	{
		if(list->data[i]==key)
		{
			return i;		//查找成功
		}
	}
	return -1;	//查找失败
}


//改进顺序查找算法
int search(List* list,int key)
{
	int i;
	list->data[0]=key;    //设置一个哨兵
	for(i=(list->num)-1;list->data[i]!=key;i--)	//倒着查找
	{
		;
	}
	return i;
}

改进之后的算法：可以少一次判断list是否会超出链表长度 

b.二分查找

操作过程：在有序表中，取中间记录作为比较对象，若给定值与中间记录的关键字相等，则查找成功；若给定值小于中间记录的关键字，则在中间记录的左半区继续查找；若给定值大于中间记录的关键字，则在中间记录的右半区继续查找。不断重复上述过程，直到查找成功，或所有查找区域无记录，查找失败。

注：二分查找的前提是线性表必须有序（通常从小到大有序）

平均查找长度：[(n+1)/n]*log2(n+1)−1

时间复杂度：O(log2n)->log以2为底n的对数

代码：

//二分查找(循环)
int binarySearch1(int key,List* list)
{
	int start=0;
	int end=list->num-1;
	int mid;
	while(start<=end)
	{
		mid=(start+end)/2;
		if(list->data[mid]data[mid]>key)
		{
			end=mid-1;
		}
		else
		{
			return mid;	
		}
	}
	return -1;	//没找到
}


//二分查找(递归)
int binarySearch2(int key,List* list,int start,int end)
{
	if(start==end)
	{
		if(list->data[start]==key)
		{
			return start;
		}
		else
		{
			return -1;
		}
	}
	int mid=(start+end)/2;
	if(list->data[mid]data[mid]>key)
	{
		return binarySearch2(key,list,start,mid-1);
	}
	else
	{
		return mid;
	}
}

c.二叉排序树

性质：

1. 若它的左子树不空，则左子树上所有的结点的值均小于它的根结点的值
2. 若它的右子树不空，则右子树上所有的结点的值均大于它的根结点的值
3. 它的左右子树也分别为二叉排序树

查找成功的平均查找长度：∑（本层高度*本层元素个数）/节点总数

查找失败的平均查找长度：∑（本层高度*本层补上的叶子个数）/补上的叶子总数

时间复杂度：O(log2n)~O(n)之间

代码：插入以及查找

#include
#include

/*
	Binary Search Tree(BST):
	一颗二叉树，左子树上的所有节点的值都比根节点小，
	右子树上的所有的节点的值都比根节点大，
	同时这个性质是递归的
	注：树中的节点的值不能重复
	
	功能:
	1.建立一个二叉排序树
	2.在二叉树中查找值
*/

typedef struct TreeNode{
	int data;
	struct TreeNode* lchild;	//左孩子
	struct TreeNode* rchild;	//右孩子
}TreeNode;

//查找
TreeNode* bstSearch(TreeNode* T,int key)
{
	if(T)
	{
		if(T->data==key)
		{
			return T;
		}
		else if(keydata)
		{
			return bstSearch(T->lchild,key);
		}
		else
		{
			return bstSearch(T->rchild,key);
		}
	}
	else
	{
		return NULL;
	}
}

void bstInsert(TreeNode** T,int key)    //使用二维指针，来改变T的指向，即改变一维指针
{
	if(*T==NULL)
	{
		*T=(TreeNode*)malloc(sizeof(TreeNode));
		(*T)->data=key;
		(*T)->lchild=NULL;
		(*T)->rchild=NULL;
	}
	else if(key==((*T)->data))
	{
		return;
	}
	else if((*T)->data>key)
	{
		bstInsert(&(*T)->lchild,key);
	}
	else
	{
		bstInsert(&(*T)->rchild,key);
	}
}

void PreOrder_Traverase(TreeNode* T)
{
	if (T == NULL)
		return;
	else
	{
		printf(" %d ", T->data);
		PreOrder_Traverase(T->lchild);
		PreOrder_Traverase(T->rchild);
	}
}

int main()
{
	TreeNode* T=NULL;
	int nums[6]={4,5,19,23,2,8};
	for(int i=0;i<6;i++)
	{
		bstInsert(&T,nums[i]);
	}
	PreOrder_Traverase(T);
	bstSearch(T,19);
	int key=19;
	TreeNode* result=bstSearch(T,key);
	printf("\n");
	if(result)
	{
		printf("查找成功：%d \n",result->data);
	}
	else
	{
		printf("查找失败\n");	
	}
	return 0;
}

二叉排序树的删除操作： 

1）删除叶子结点上

        直接删除即可

2） 删除只有左子树的结点 （删除只有右子树的结点）：即只有一个叶子结点

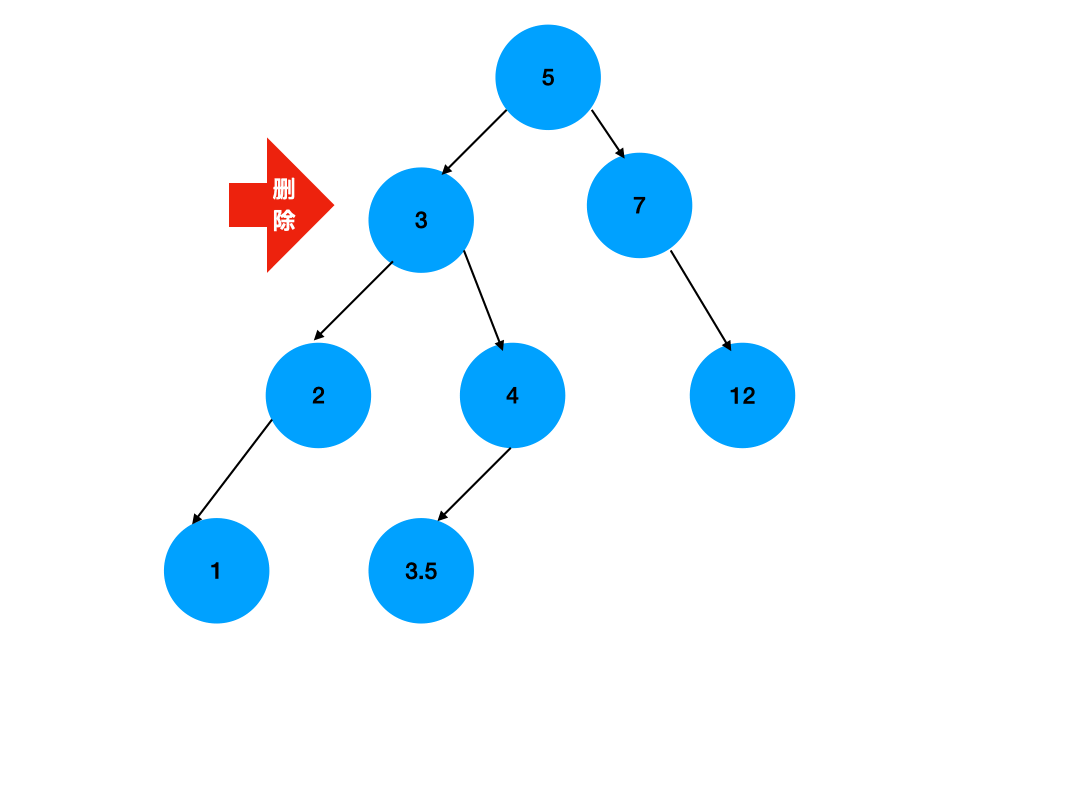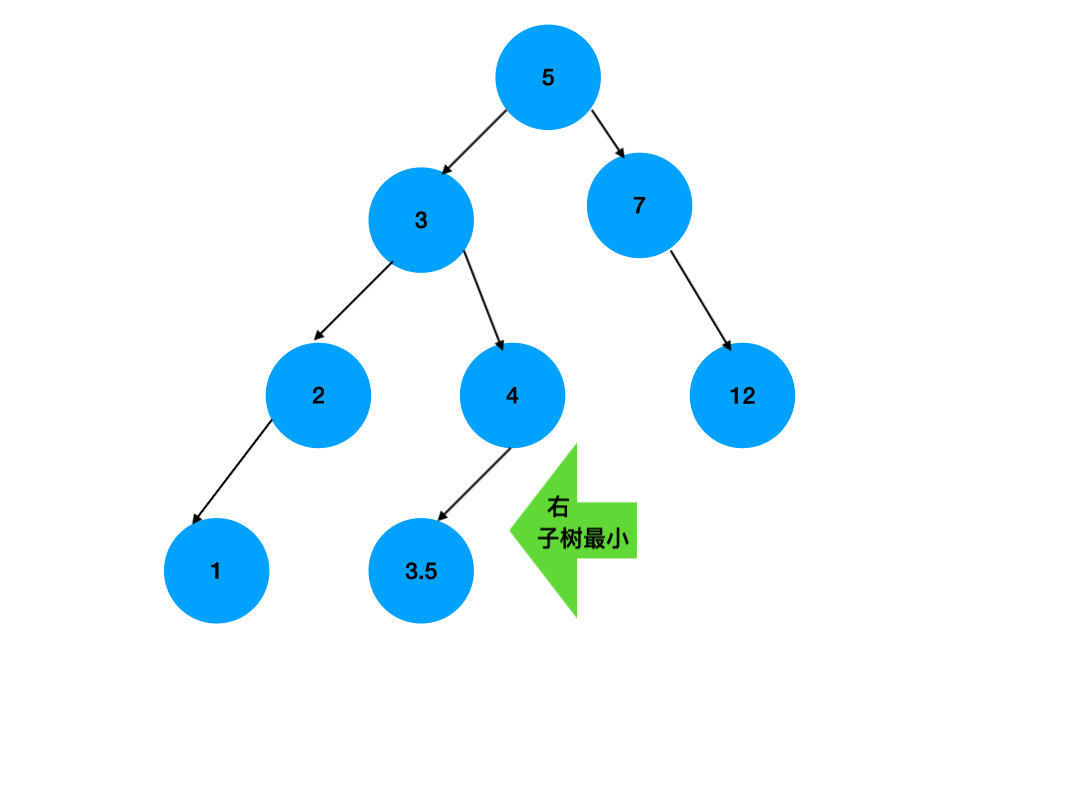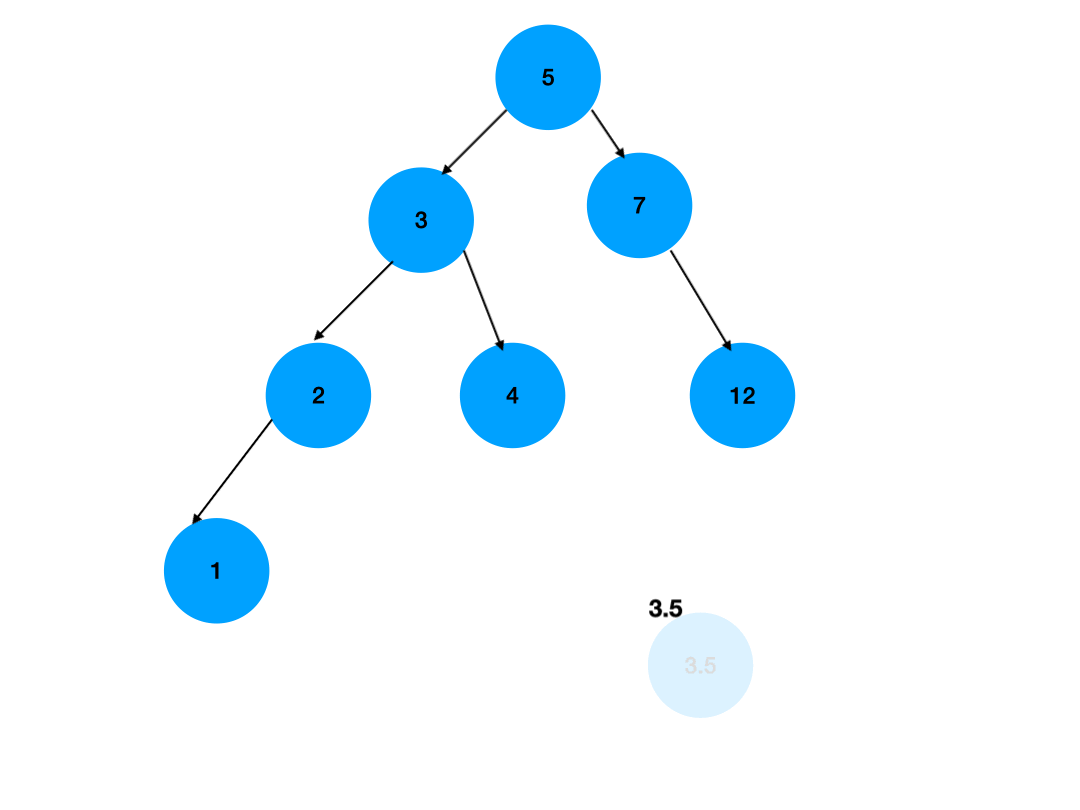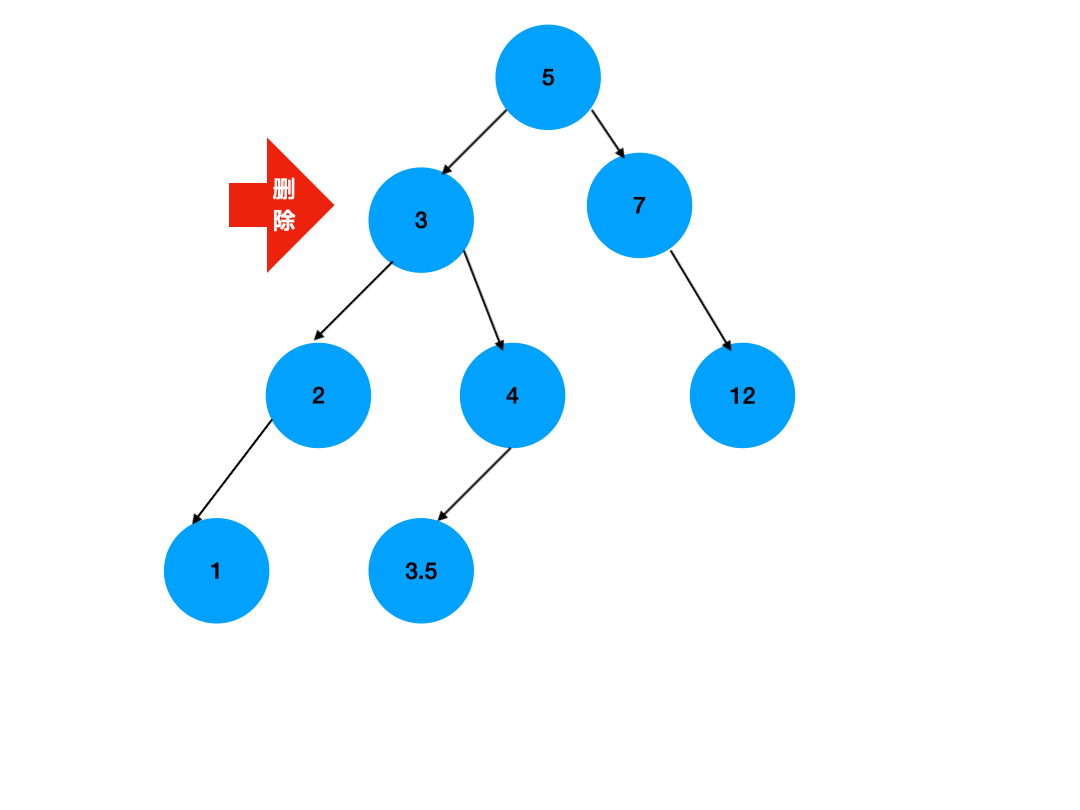
 4） 删除左右子树均不空的结点 

d.哈希表

注：由于本博主觉得自己哈希表的知识点整理的不太好，所以找了两个不错的连接

哈希表的知识点：

数据结构探究：哈希表（Hash）相关知识点_浅亡的博客-CSDN博客

各种不同方式处理散列冲突的方法：

哈希表等查找成功和查找不成功的平均查找长度（线性探测法+链地址法）_Zzz小白飞的博客-CSDN博客

哈希表：线性探测法和链地址法求查找成功与不成功的平均查找长度_职业发报员的博客-CSDN博客_线性探测法查找失败的平均查找长度 

代码：

#include
#include

#define NUM 5

typedef struct HashList{
	int num;
	char* data; 
}HashList;

//初始化哈希表
HashList* initHashList()
{
	HashList* list=(HashList*)malloc(sizeof(HashList));
	list->num=0;
	list->data=(char*)malloc((sizeof(char)*NUM));
	for(int i=0;idata[i]=0;
	}
	return list;
}

//哈希函数
int hash(int data)
{
	return data%NUM;	
}

//线性探测法
void put(HashList* list,char data)
{
	int index=hash(data);
	if(list->data[index] != 0)
	{
		int count=1;
		while(list->data[index] !=0)
		{
			index=hash(hash(data)+count);
			count++;
		}
	}
	list->data[index]=data;
	list->num++;
}

int main()
{
	HashList* list=initHashList();
	put(list,'A');
	put(list,'F');
	printf("%c\n",list->data[0]);
	printf("%c\n",list->data[1]);
	return 0;
}

e.平衡二叉树