312.戳气球（java）

题目描述

有 n 个气球，编号为0 到 n-1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。如果你戳破气球 i ，就可以获得 nums[left] * nums[i] * nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后，气球 left 和气球 right 就变成了相邻的气球。

求所能获得硬币的最大数量。

说明:

• 你可以假设 nums[-1] = nums[n] = 1，但注意它们不是真实存在的所以并不能被戳破。
• 0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100

示例:

输入: [3,1,5,8]
输出: 167 
解释: nums = [3,1,5,8] --> [3,5,8] -->   [3,8]   -->  [8]  --> []
     coins =  3*1*5      +  3*5*8    +  1*3*8      + 1*8*1   = 167

---

解法一：回溯法（超时）

只要涉及求最值，没有任何奇技淫巧，一定是穷举所有可能的结果，然后对比得出最值。

穷举主要有两种算法，就是回溯算法和动态规划，前者就是暴力穷举，而后者是根据状态转移方程推导「状态」。

public static void maxCoins2(int[] nums, int y, int length, int beforeCoins) {
        //回归条件
        if (y == length) {
            if (beforeCoins > maxCoin) {
                maxCoin = beforeCoins;
            }
            return;
        }
        for (int i = 0; i < length; i++) {
            //略过已经戳破的气球
            if (nums[i] == -1) {
                continue;
            }
            //标记已经戳破的气球
            int temp = nums[i];
            nums[i] = -1;
            //获取上一个气球的数字
            int before = i - 1;
            int beforeNum = 0;
            while (before > -1 && nums[before] == -1) {
                before--;
            }
            if (before < 0) {
                beforeNum = 1;
            } else {
                beforeNum = nums[before];
            }
            //获取下一个气球的数字
            int next = i + 1;
            int nextNum = 0;
            while (next < length && nums[next] == -1) {
                next++;
            }
            if (next > length - 1) {
                nextNum = 1;
            } else {
                nextNum = nums[next];
            }
            //计算戳破当前气球的coin
            int tempCoin = temp * nextNum * beforeNum;
            //递归进行下一戳
            maxCoins2(nums, y + 1, length, beforeCoins + 
            tempCoin);
            //回溯尝试其它戳法
            nums[i] = temp;
        }
    }

每层有n中选择，第i层有n-i中选择，时间复杂度为n*(n-1)*(n-2)…*1即 !n。n的阶乘，指数级的时间复杂度

---

解法二：分治法

子问题该如何划分才能通过子问题来求解原问题。

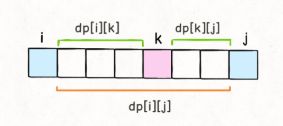
def( i , j ) 函数的定义为，不戳破 i 与 j ，仅戳破 i 与 j 之间的气球我们能得到的最大金币数。

状态转移方程为： def( i, j ) = def( i , k ) + def( k , j )+nums [ i ] [ j ] [ k ]

事实上，我们尝试所有 k 的取值并从中挑选最大值，这才是原问题真正的解。

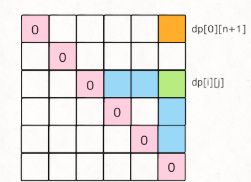
真正的状态转移方程应该为：def( i, j ) = max { def( i , k ) + def( k , j )+nums[ i ] [ j ] [ k ] } | i

回归条件 def( i , i+1 ) = 0

public static int maxCoins4(int[] nums, int length, int begin, int end,int[][] cache) {
        //回归条件，问题分解到最小子问题
        if (begin == end - 1) {
            return 0;
        }
        //缓存，避免重复计算
        if(cache[begin][end]!=0){
            return cache[begin][end];
        }
        //维护一个最大值
        int max = 0;
        //状态转移方程 def( i, j ) = max { def( i , k ) + def( k , j )+nums[ i ][ j ][ k ] } | i
        for (int i = begin + 1; i < end; i++) {
            int temp = maxCoins4(nums, length, begin, i,cache) +
                    maxCoins4(nums, length, i, end,cache) + nums[begin] * nums[i] * nums[end];
            if (temp > max) {
                max = temp;
            }
        }
        //缓存，避免重复计算
        cache[begin][end]=max;
        return max;
    }
 
我们再封装一层方法，对空数组进行处理。因为 def( i , j ) 并不戳破两个边界的气球，我们为气球数组加上虚拟的边界：
 
    public static final int maxCoins4MS(int[] nums) {
        //空数组处理
        if (nums == null) {
            return maxCoin;
        }
        //加虚拟边界
        int length = nums.length;
        int[] nums2=new int[length+2];
        System.arraycopy(nums,0,nums2,1,length);
        nums2[0]=1;
        nums2[length+1]=1;
        length=nums2.length;
        //创建缓存数组
        int[][] cache=new int[length][length];
        //调用分治函数
        return maxCoins4M(nums2, length,cache);
    }

    public static int maxCoins4M(int[] nums, int length,int[][] cache) {
        int max = maxCoins4(nums, length, 0, length - 1,cache);
        return max;
    }

---

解法三：动态规划

实现中还存在着递归调用。递归调用的效率是很低的，们应该去思考递归调用的回归过程，通过模拟回归过程来用递推实现上述代码。

对于动态规划而言，同层级的子问题可能会依赖相同的低层级问题，这就导致低层级问题可能会被计算多次。

可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。

这个问题中我们每戳破一个气球 nums[i]，得到的分数和该气球相邻的气球 nums[i-1] 和 nums[i+1] 是有相关性的。

分析思路

具有最优子结构性质以及重叠子问题性质的问题可以通过动态规划求解。

最优子结构
• 如果一个问题的最优解包含其子问题的最优解，我们就称此问题具有最优子结构
• 一个问题具有最优子结构，可能使用动态规划方法，也可能使用贪心方法。所以最优子结构只是一个线索，不是看到有最优子结构就一定是用动态规划求解

重叠子问题
• 子问题空间必须足够“小”，即在不断的递归过程中，是在反复求解大量相同的子问题，而不是每次递归时都产生新的子问题。
• 一般的，不同子问题的总数是输入规模的多项式函数为好
• 如果递归算法反复求解相同的子问题，我们就称最优化问题具有重叠子问题性质

对于前面的分治解法，我们的计算过程分为两个阶段：
1、递归的不断的分解问题，直到问题不可继续分解。
2、当问题不可继续分解，也就是分解到最小子问题后，由最小子问题的解逐步向上回归，逐层求出上层问题的解。

阶段1我们称为递归过程，而阶段2我们称为递归调用的回归过程。我们要做的，就是省略递归分解子问题的过程，将阶段2用递推实现出来。

举例

dp[0] [4] =max { dp[0] [1]+dp[1] [4]+nums[0]*nums[1]*nums[4] , dp[0] [2]+dp[2] [4]+nums[0]nums[2]nums[4] , dp[0] [3]+dp[3] [4]+nums[0] nums[3] nums[4] }

标红部分没有达到回归条件，会继续向下分解，以 dp[1] [4] 为例：

dp[1] [4]= max { dp[1] [2]+dp[2] [4]+nums[1]* nums[2] * nums[4] , dp[1] [3]+dp[3] [4]+nums[1]* nums[3]* nums[4] }

标红部分继续分解：

dp[2] [4]= dp[2] [3] + dp[3] [4] + nums[2]* nums[3]* nums[4]
dp[1] [3] = dp[1] [2] + dp[2] [3] + nums[1]* nums[2]* nums[3]

状态方程

dp[i] [j] = dp[i] [k] + dp[k] [j] + points[i]* points[k]* points[j]

写出代码

关于「状态」的穷举，最重要的一点就是：状态转移所依赖的状态必须被提前计算出来。

在计算 dp[i][j] 时，dp[i][k] 和 dp[k][j] 已经被计算出来了（其中 i < k < j）。

对于任一 dp[i][j]，我们希望所有 dp[i][k] 和 dp[k][j] 已经被计算，画在图上就是这种情况：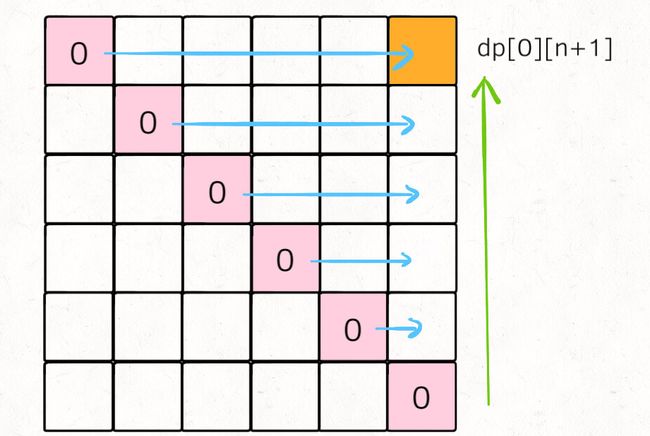

那么，为了达到这个要求，可以有两种遍历方法，要么斜着遍历，要么从下到上从左到右遍历

class Solution {
    public int maxCoins(int[] nums) {
        int n = nums.length;
        //创建虚拟节点
        int[] arr = new int[n+2];
        arr[0]=arr[n+1]=1;
        for(int i=0;i<n;i++){
            arr[i+1]=nums[i];
        }
        int[][] dp = new int[n+2][n+2];
        //动态规划
        //从下往上
        for(int i=n;i>=0;i--){
            //从左往右
            for(int j=i+1;j<n+2;j++){
                //逐个尝试
                for(int k=i+1;k<j;k++){
                    //找出最值
                    dp[i][j]=Math.max(dp[i][j],dp[i][k]+dp[k][j]+arr[i]*arr[k]*arr[j]);
                }
            }
        }
        return dp[0][n+1];
    }
}