力扣 --- 三数之和

目录

题目描述：

思路描述：

代码：

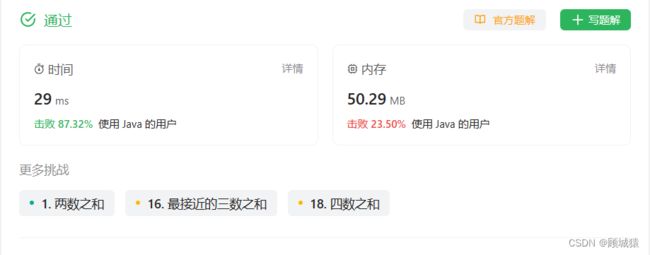
提交结果：

官方代码：

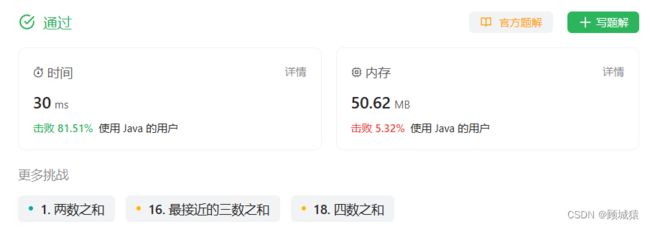
官方提交结果：

---

题目描述：

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

思路描述：

        对于这个题，我们很容易想到一个非常简单的方法，就是用三层遍历，每一层代表一个数，暴力求解所有结果，选出其中符合条件的组合。此方法虽然简单，但是，时间复杂度比较高，因此，该方法用于提交力扣，是通不过的。

        我们可以换一种其他的思路，我们可以将其转换成，两个数之和为另一个数的相反数的思路来解决这个题目。

        第一个索引表示第一个数，从前往后遍历，要遍历到倒数第三个，因为遍历到倒数第一第二的位置，是没有必要的，因为不够三个的数目。

        第二个索引表示第二个数，初始为第一个数的下一位索引，第三个索引表示第三个数，初始为数组末端的元素，从第二个索引和第三个索引之间的位置找出两个数的和为第一个数的相反数的两个数。

        如何操作第二和第三索引？如果数组是有序的，我们很容易来遍历，即两个索引的元素之和大于第一个数的相反数，就让第三索引减小，如果等于，说明是一个符合条件的组合，如果小于，就让第二索引增加。

        因此，开头，我们要现将数组进行排序，这样，后续操作就变的非常简单。

代码：

class Solution {
    public List> threeSum(int[] nums) {
        List> result=new ArrayList<>();
        Arrays.sort(nums);//排序
        for(int i=0;i0 && nums[i]==nums[i-1]){
                continue;
            }
            if(nums[i]>0){//第一数是整数，就无须再遍历
                break;
            }
            int item=-nums[i];
            int left=i+1;
            int right=nums.length-1;
            while(left myList=new ArrayList<>();
                    myList.add(nums[i]);
                    myList.add(nums[right]);
                    myList.add(nums[left]);
                    result.add(myList);
                    while(leftleft && nums[right]==nums[right-1]){
                        right--;
                    }
                    right--;
                }else if(nums[left]+nums[right]

提交结果：

官方代码：

class Solution {
    public List> threeSum(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums);
        List> ans = new ArrayList>();
        // 枚举 a
        for (int first = 0; first < n; ++first) {
            // 需要和上一次枚举的数不相同
            if (first > 0 && nums[first] == nums[first - 1]) {
                continue;
            }
            // c 对应的指针初始指向数组的最右端
            int third = n - 1;
            int target = -nums[first];
            // 枚举 b
            for (int second = first + 1; second < n; ++second) {
                // 需要和上一次枚举的数不相同
                if (second > first + 1 && nums[second] == nums[second - 1]) {
                    continue;
                }
                // 需要保证 b 的指针在 c 的指针的左侧
                while (second < third && nums[second] + nums[third] > target) {
                    --third;
                }
                // 如果指针重合，随着 b 后续的增加
                // 就不会有满足 a+b+c=0 并且 b list = new ArrayList();
                    list.add(nums[first]);
                    list.add(nums[second]);
                    list.add(nums[third]);
                    ans.add(list);
                }
            }
        }
        return ans;
    }
}

官方提交结果：