【刷题笔记】长度最小的子数组||二分查找||边界||数组

长度最小的子数组

1 题目描述

https://leetcode.cn/problems/minimum-size-subarray-sum/

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

进阶：如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

2 思路

2.1 整体架构

因为前几天做二分查找做魔怔了，导致我一上来就想着用二分，根本没想到O(n)时间复杂度的双指针法。

O(n)时间复杂度的做法

接下来讲述使用O(n log (n))时间复杂度的做法。

如上图，假设我们有一个子串（黄色部分），黄色子串的总和为Sum，我们可以从黄色子串中寻找一个更小的绿色子串（和为Sum_sub），我们要让这个绿色子串满足Sum - Sum_sub >= target，如果绿色子串尽可能的长，那么黄色子串去除绿色子串之后剩余的子串就尽可能地短。

我们看题目要求，n个正整数，这说明了当我们对每个位置i及其之前的元素进行加和，获得一个新的数组sum_list，那么sum_list[i]>sum_list[i-1]，这说明sum_list是一个单调递增数组。

假设我们的黄色数组为nums[0:i+1] （0~i索引对应的元素构成的子串）。我们则需要在nums[0:1]到nums[0:i] 这些数组中找到长度最大的并且满足要求的数组nums[0:t+1]（索引从0到t的元素构成的数组）。它们满足sum_list[i] - sum_list[t] >= target。

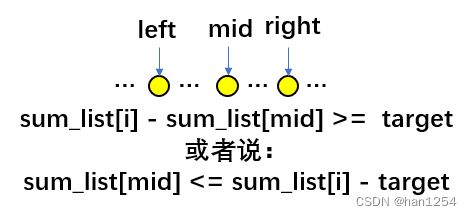
翻译一下，其实就是当我们在遍历到i的时候，需要从sum_list[0]~sum_list[i-1]中找到一个索引t，满足sum_list[i] - sum_list[t] >= target，这说明nums[t + 1]~nums[i]的和大于等于target，而sum_list[i] - sum_list[t + 1] < target。

即，当最外部索引为i的时候，我们需要从sum_list[0] ~ sum_list[i - 1]中寻找满足sum_list[i] - sum_list[j] >= target的右边界索引t。

首先我们计算sum_list：

int more_index = -1;
int min_len = nums.length;
int[] sum_list = new int[nums.length];
int sum = 0;
for (int i = 0; i < nums.length; i++) {
    sum += nums[i];
    sum_list[i] = sum;
    if (sum >= target){
        if (more_index < 0) more_index = i;
    }
}
if (more_index == -1) return 0;

此时，more_index是为了记录第一个大于等于target的坐标。因为如果sum_list[i] < target没有意义，不可能在0~i中找到一个大于等于target的子串，因为整个数组全部为正整数。

如果整个数组中没有和能够大于等于target的子串，直接返回0。

假设我们现在已经有了一个二分查找的函数，那么我们如何续写接下来的代码呢？

如果我们已经通过二分查找获得了当前sum_list[0:i]子串（这是python的切片风格，表示从0~(i-1)的子串）中，最后一个满足sum_list[i] - sum_list[j] >= target的下标t，如果没找到，返回-1。

如果找到了，那么满足条件的数组长度为i-j，如果返回-1，也照样减去，因为返回-1后，说明只有nums[0:i+1]满足条件，这样的子串的长度是i-(-1) = i+1，也就是说无论返回什么值，我们只需要计算i-j就是满足需求的子串长度了。

接下来我们继续看关键的二分查找部分。

2.2 二分查找设计

这里，我沿用前几篇博客的思路

【刷题笔记】两数之和II_二分法||二分查找||边界||符合思维方式

【刷题笔记】H指数||数组||二分查找的变体

对于二分查找有两个最重要的问题：如何计算mid，如何跳转left和right。

这个两个问题本身是一个问题，只要我们确定了如何跳转left和right，就能确定如何计算mid。

通过我们上一节的分析，我们知道，这个查找是一个边界问题，查找符合条件的右边界。

left往右移，所以我们用left来找右边界。

当mid满足条件的时候，我们不清楚mid右边的元素是否还满足条件，我们的left最多就是跳转到mid上。

如果mid不满足条件，则说明mid位置对应的元素过大了，mid一定不满足，mid左边还是有可能的。所以right会跳转到mid-1的位置。

我们知道了left会转移到mid上，那么接下来考虑mid的计算。

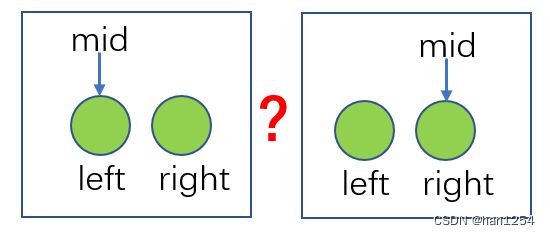
众所周知，当我们在只剩下两个元素的时候，mid元素要么是(left + right) / 2，放在left上，要么是(left + right) / 2 + 1，放在right上。

我们已经确定了，left在某些条件下是可能直接跳转到mid上的， 如果让mid=left，下一步如果left需要跳转，left=mid，然后mid=left。。。。。。无限循环。

所以，为了避免死循环，当只有偶数个元素的时候，我们需要让mid跳转到中间两个元素的后一个元素上。所以我说，当我们确定了left和right的跳转问题之后，如何计算mid的问题就迎刃而解。

面对二分问题的时候，left和right的取值，我倾向于直接使用真实位置，即从1开始的位置。
（以上文字也可以在前面给出的博客链接中看到，我期待能够找到一种通用的范式，所以会尽量使用重复文字，不是偷懒）

public int biSearch(int other_tar, int[] sumlist, int start, int end) {
    // 参数里面的other_tar其实就是sum_list[i] - target
    // start和end就是需要进行搜索的数组的开始下标和结束下标。
    int left = start + 1, right = end + 1;
    while (left < right) {
        int real_mid = (left + right) / 2 + ((left - right + 1) % 2 == 0 ? 1 : 0);
        // 如果l~r的元素个数为奇数个，(l+r) / 2 就是中间元素的真实位置
        // 如果l-r的元素个数为偶数个，(l+r) / 2 就是中间两个的元素的靠左的元素，所以要+1
        // 变成中间两个元素靠右的位置。
        int mid_index = real_mid - 1; // 索引要比真实位置-1。
        if (sumlist[mid_index] <= other_tar) {
            left = real_mid;
        } else {
            right = real_mid - 1;
        }
    }
    // 看看我们找到的元素是不是真的满足条件，还是说数组中根本没有满足条件的元素
    return (sumlist[left - 1] <= other_tar ? left - 1 : -1); 
}

3 代码

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int more_index = -1;
        int min_len = nums.length;
        int[] sum_list = new int[nums.length];
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            sum_list[i] = sum;
            if (sum >= target){
                if (more_index < 0) more_index = i;
            }
        }
        if (more_index == -1) return 0;
        for (int i = more_index; i < nums.length; i++) {
            int res_pos = biSearch(sum_list[i] - target, sum_list, 0, i - 1);
            min_len = Math.min(i - res_pos, min_len);
        }
        return min_len;
    }

    public int biSearch(int other_tar, int[] sumlist, int start, int end) {
        int left = start + 1, right = end + 1;
        while (left < right) {
            int real_mid = (left + right) / 2 + ((left - right + 1) % 2 == 0 ? 1 : 0);
            int mid_index = real_mid - 1;
            if (sumlist[mid_index] <= other_tar) {
                left = real_mid;
            } else {
                right = real_mid - 1;
            }
        }
        return (sumlist[left - 1] <= other_tar ? left - 1 : -1);
    }
}