字典树-Trie详解

问题导入：

假如现在有n个单词在一个集合里面，将集合记为S，有m个询问，每次询问为一个单词，询问该单词是否在这个集合内?

什么是Trie树(字典树)：

Trie树是一种数据结构，顾名思义它是一棵树，每个节点是一个字符，比如说是一个字母或者一个数字等等。我们可以利用每个字符串的公共前缀来构建出一棵树，例如： 

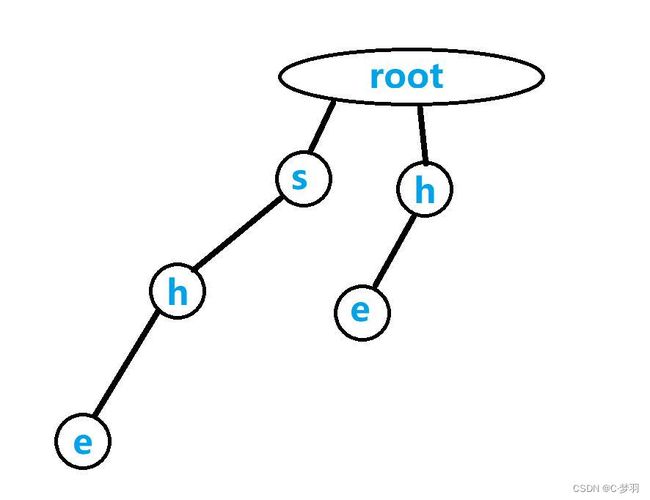
现在有5个字符串：{"she","he","say","shr","her"}，我们可以按顺序来先画出第一个字符串's','h','e'三个节点以及一个空的根节点：

再画出'h','e'两个节点，必须要从根root开始画，如下：

 接着，画出"say"这个字符串，由于从根节点有一条到's'的边，所以从后面接着画：

然后，是"shr"这个字符串，规则同上：

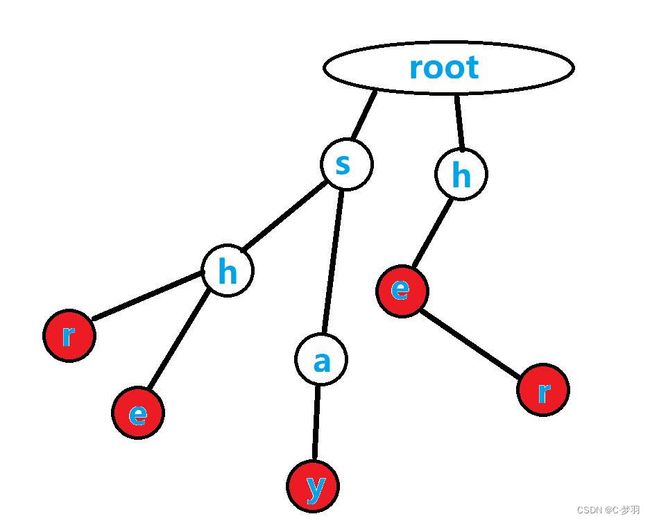
最后，把"her"加上，我们的Trie树就构建成功了！！！

 

只需把出现过的单词的路径的最后一个字母标红，就表示该单词在这个字典树中出现过，比如说如果我们想要查询"say"这个单词的存在性，先从根节点root开始，由于有一条连向's'节点的边，我们第一步先走到's'节点，再比对第二个字母'a' ，我们可以发现从当前的节点's'也有到'a'节点的边，所以可以继续走下去，最后走到了'y'这个节点，由于'y'节点有被标红，所以"say"这个单词存在。

反例："sa"这个单词不存在，虽然有路径存在，但是最后一个节点'a'没有被标红。

字典树的优势：

如果每个节点是一个小写字母，对于一个单词集，由于公共前缀的利用，所以Trie树的层数不会很多，如果层数为n，那么查找的效率是log(n)的，非常高效。

字典树的实现：

1、下标idx，每个节点都有一个下标，比如上述先建立单词"she"，'s'节点的下标是1，'h'节点的下标是2，'e'节点的下标是3，以此类推......

2、tr[i][j]，表示下标为i的节点下一个节点j是否存在，如果tr[i][j]=0的话，就是说下标为i的点没有连向j的一条路径，例如：在上述情况下，tr[2]['r']=1，表示's'节点后面有连有'r'的路径。

3、cnt[i]，表示下标为i的节点是否被标红，如果cnt[i]=1，表示以下标为i的节点有一个在集合内的单词，例如：cnt[3]=1，表示单词"she"存在。

4、字典树支持插入和查询操作。

字典树的insert操作：

void insert(char str[])
{
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u])son[p][u]=++idx;
        p=son[p][u];
    }
    cnt[p]++;
}

字典树的查询操作：

int query(char str[])
{
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u])return 0;
        p=son[p][u];
    }
    return cnt[p];
}

模板题：

题目描述： 

维护一个字符串集合，支持两种操作：

1、I x 向集合中插入一个字符串 x；

2、Q x 询问一个字符串在集合中出现了多少次。

共有 N 个操作，输入的字符串总长度不超过 10^5，字符串仅包含小写英文字母。

输入格式：

第一行包含整数 N(1≤N≤2*10^4)，表示操作数。

接下来 N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式：

对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x 在集合中出现的次数。

每个结果占一行。

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

参考代码:

#include
using namespace std;
const int N=100010;
int n,idx;
int son[N][26],cnt[N];
char str[N];
void insert(char str[])
{
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u])son[p][u]=++idx;
        p=son[p][u];
    }
    cnt[p]++;
}
int query(char str[])
{
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u])return 0;
        p=son[p][u];
    }
    return cnt[p];
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++){
        char op[2];
        scanf("%s%s",op,str);
        if(*op=='I')insert(str);
        else cout<

结语： 

关于 字典树-Trie的详解就到这里。