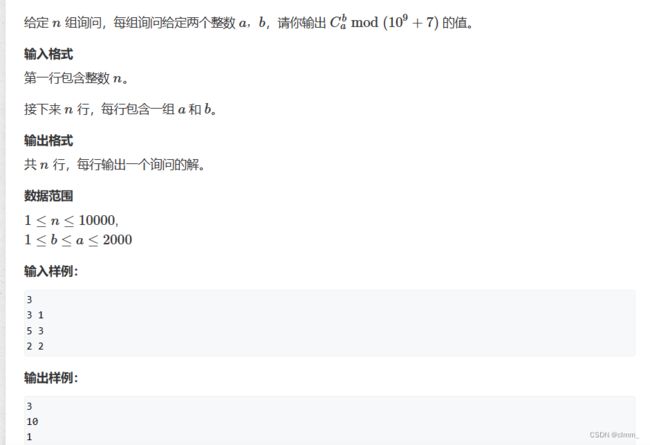
组合数学（四种求组合数的方法：递推，逆元，lucas，卡特兰数）
求组合数，对于不同的数据量可以用不同的方法。实际上只用记住最高效的那个方法即可。本文将介绍四种求组合数的办法
递推求组合数
我们需要知道一个递推式。
怎么记忆呢？
假如我们要求从a个苹果里选b个苹果，我们可以分成两种情况
1.包含a个苹果里的苹果i（ai），那么就是
，因为已经选了ai，再选b-1个苹果即可
2.不包含ai，就是
，需要在剩下的a-1个苹果里选b个苹果
用递推式预处理，时间复杂度就大大降低了
时间复杂度O(
)
int ans[2010][2010];
int mod = 1e9 + 7;
void init() {
for(int i = 1;i<=2005;i++){
for (int j = 0; j <= i; j++) {
if (i == j || j == 0) {
ans[i][j] = 1;
}
else {
ans[i][j] = (ans[i - 1][j] + ans[i - 1][j - 1]) % mod;
}
}
}
}
signed main() {
int n; cin >> n;
init();
while (n--) {
int a, b; cin >> a >> b;
cout << ans[a][b] << endl;
}
return 0;
}逆元求组合数
可以看到数据变大了,再用第一种的O()就过不了了
分析：时间复杂度O(
)。预处理。
const int N = 1e6 + 10;
long long MAX(long long a, long long b) { return a < b ? b : a; }
long long MIN(long long a, long long b) { return a < b ? a : b; }
int qmi(int a, int k, int p) {
int res = 1;
while (k) {
//后面的a其实是底数与其指数的运算结果了，是不断迭代的
//第一个a其实就是a的2的0次方
if (k & 1) res = (res * a) % p;
a = (a * a) % p;
//注意，a是一个不断变化的过程
//下一个a就等于上一个a的平方，
k >>= 1;
}
return res;
}
int mod = 1e9 + 7;
int fact[N], infact[N];
void init() {
//注意！0的阶乘和逆元是1！
fact[0] = 1; infact[0] = 1;
for (int i = 1; i <= N; i++) {
fact[i] = fact[i - 1] * i % mod;
infact[i] = infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
}
signed main() {
init();
int t; cin >> t;
while (t--) {
int a, b; cin >> a >> b;
cout << fact[a] % mod * infact[b] % mod * infact[a - b] % mod << endl;
}
return 0;
}有个疑惑，不能直接用定义求吗？毕竟数最大才1e5，算上快速幂的时间复杂度，
也只是O()。
错！观察一下，最多有10000个测试样例，因此会超时，肯定需要预处理的
int C(int a, int b) {//这个就是根据定义求组合数
int ans = 1;
int j = a;
for (int i = 1; i <= b; i++,j--) {
ans = ans * j % mod;
ans = ans * qmi(i, mod - 2, mod) % mod;
}
return ans;
}Lucas定理求组合数
定理内容
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
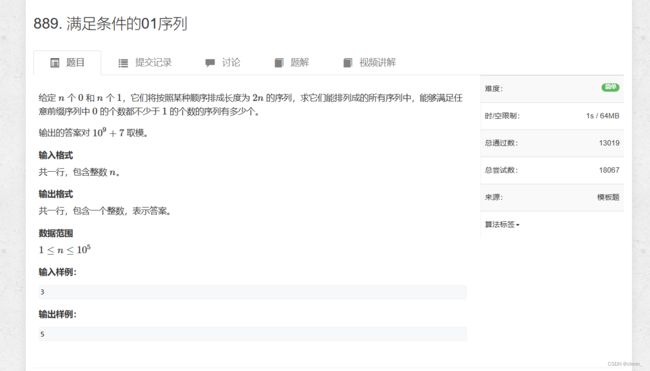
卡特兰数求组合数
结合一道例题来理解知识点
分析：有n个0和n个1，排列成一个序列，使其任意前缀序列中0的个数不少于1的个数
我们可以画一张表格，0代表向右走一格，1代表向上走一格，从（0，0）出发，最后会走到（n，n）。从（0，0）到（n，n）的走法有
。（从2n步里挑n步向上走）
我们想满足“前缀序列中0的个数不少于1的个数”，即cnt_0 >= cnt_1，代表“向右走的次数>=向上走的次数”，所以走的路径只能在红线以下，如果走到红线上以及其上方就是不合法的走法。
因此 合法的走法数 = 总走法数 - 不合法的走法数。
不合法的走法数怎么求？这里有一个小规律：如果一个走法不合法，那么其路径一定会走到红线上方。这时候把红线上方的路径关于红线做轴对称，会发现终点在始终在（n-1，n+1）。
因此 从（0，0）到（n-1，n+1）的走法 = 不合法的走法 = 
= 
（挑n-1步向右走或挑n+1步向上走）
所以 ans = - = 
（经过一系列推导得来）
int qmi(int a, int k, int p) {
int res = 1;
while (k) {
//后面的a其实是底数与其指数的运算结果了，是不断迭代的
//第一个a其实就是a的2的0次方
if (k & 1) res = (res * a) % p;
a = (a * a) % p;
//注意，a是一个不断变化的过程
//下一个a就等于上一个a的平方，
k >>= 1;
}
return res;
}
int C(int a, int b,int p) {
int ans = 1;
int j = a;
for (int i = 1; i <= b; i++,j--) {
ans = ans * j % p;
ans = ans * qmi(i, p - 2, p) % p;
}
return ans;
}
int lucas(int a, int b,int p) {
if (a < p && b < p) {
return C(a, b, p);
}
return C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
const int mod = 1e9 + 7;
signed main()
{
int n; cin >> n;
cout << lucas(2 * n, n, mod) % mod * qmi(n + 1, mod - 2, mod) % mod;
return 0;
}