DS八大排序之直接选择排序和堆排序
前言
上一期我们已经介绍了,排序、为什么要有排序以及排序在实际生活中的应用。并且介绍并实现了直接插入排序和它的优化即希尔排序~!本期我们再来学习一组排序 ---- "选择排序"即直接选择排序和堆排序~!
本期内容介绍
直接选择排序
堆排序
选择排序的基本思想
每次从待排序的数据元素的序列中选出最小或最大的一个元素,存放在当前序列的起始位置,直到将全部待排序的数据元素排完。
直接选择排序
在元素集合a[i].....a[n-1]中,选择一个最大或最小的数据,如果他不是这个序列中的最后一个或第一个,则与该序列中的最后一个或第一个进行交换,将剩余的元素重复上述操作,直到序列的元素只有一个则结束!
OK,举个栗子画个图(这里是以升序距离的):
OK,直接选择排序的过程就是这样的,下面我们来实现一下:还是和以前一样,先写单趟再来改造整体:
单趟
int left = begin;//当前序列的最左端
int min = begin;//最小的元素的下标
for (int i = begin; i < n; i++)
{
if (a[min] > a[i])
min = i;
}
Swap(&a[left], &a[min]);//最左端的元素与当前序列中最小的元素交换整体
直接选择排序改造整体也很简单,只需要,让每个元素都重复单趟即可~!
void SelectSort(int* a, int n)
{
for (int begin = 0; begin < n; begin++)
{
int left = begin;//当前序列的最左端
int min = begin;//最小的元素的下标
for (int i = begin; i < n; i++)
{
if (a[min] > a[i])
min = i;
}
Swap(&a[left], &a[min]);//最左端的元素与当前序列中最小的元素交换
}
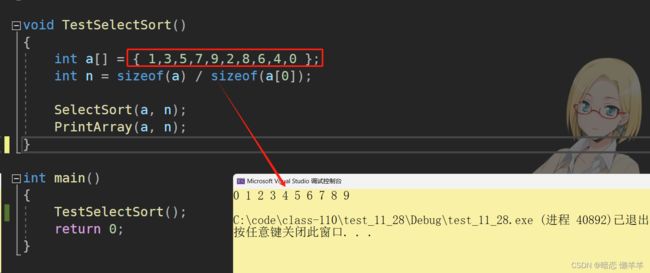
}OK,测试一下:
OK,没有问题。这样写实每次找到当前序列中最小的一个,然后与最左端(升序)交换,我们其实可以对他进行一个小优化的--->每次找到当前序列中的两个元素(一个最小,一个最大),最小的与当前序列的最左端交换,最大与当前序列的最右端交换~!
OK,还是先写单趟,在改造多趟:
单趟
int min = begin, max = begin;
for (int i = begin + 1; i <= right; i++)
{
if (a[min] > a[i])
min = i;//选出最小
if (a[max] < a[i])
max = i;//选出最大
}
Swap(&a[begin], &a[min]);//最小与左端交换
Swap(&a[right], &a[max]);//最大与右端交换整体
void SelectSort(int* a, int n)
{
int begin = 0, right = n - 1;
while (begin < right)
{
int min = begin, max = begin;
for (int i = begin + 1; i <= right; i++)
{
if (a[min] > a[i])
min = i;
if (a[max] < a[i])
max = i;
}
Swap(&a[begin], &a[min]);
Swap(&a[right], &a[max]);
++begin;
--right;
}
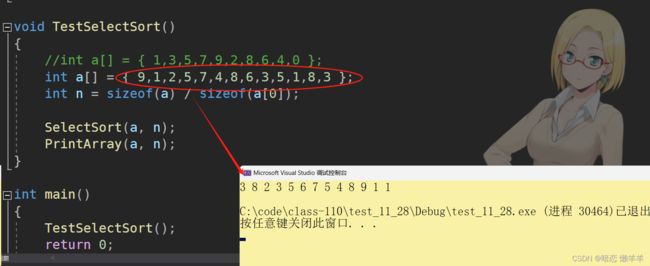
}这就是一次选出两个的整体。OK,我们来个栗子测试一下:
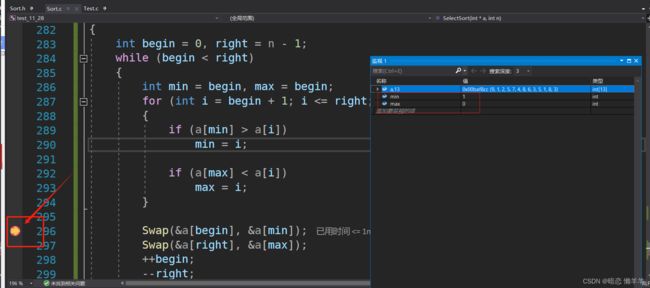
怎么没有实现排序呢?是我们的思想有问题???OK,遇事不慌,调试走起:
这是调试找到的第一次最大和最小的元素的下标~!然后下来就是最小与左端交换,最大与右端交换,但此时最大恰好在最左端,一执行最小与最左端交换后在在执行在最大与最右交换时发现最大的已经不在原来的位置了~!这就导致了上述的乱序!
解决方案:在交换完最小与最左端后,判断一下最大的位置,如果最大的是在最左端,则此时最大值应该被换到了最小值的位置,因此,我们只需要调整一下最大值是在最小值的位置即可,即max = min~!
void SelectSort(int* a, int n)
{
int left = 0, right = n - 1;
while (left < right)
{
int min = left, max = left;
for (int i = left + 1; i <= right; i++)
{
if (a[min] > a[i])
min = i;
if (a[max] < a[i])
max = i;
}
Swap(&a[left], &a[min]);
if (max == left)
max = min;
Swap(&a[right], &a[max]);
++left;
--right;
}
}再来测试一下:
OK,没有问题了~!
复杂度分析
时间复杂度:O(N^2)
单趟无论选择一个还是选择两个,都得遍历一遍,复杂度为O(N),整体还得遍历一遍O(N)
空间复杂度:O(1)
堆排序
堆排序其实在前面的二叉树堆那里已经介绍并实现过了,这来就等于回顾式的再过一遍~!如果想了解堆这种他是具体咋搞的请点击:二叉树的实现
堆排序(Heapsort)是指利用堆,这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据进行实现排序的。
他既然是借助堆来实现的那得有堆,即要建堆。这里有两种建堆的方式:向上调整建堆+向下调整排序,向下调整建堆+向下调整排序!
他排序是采用删除的思想,把最大或最小的换到最后,然后对前N-i(i=1,2,3...n)个进行向下调整!
注意:升序建大堆,降序建小堆
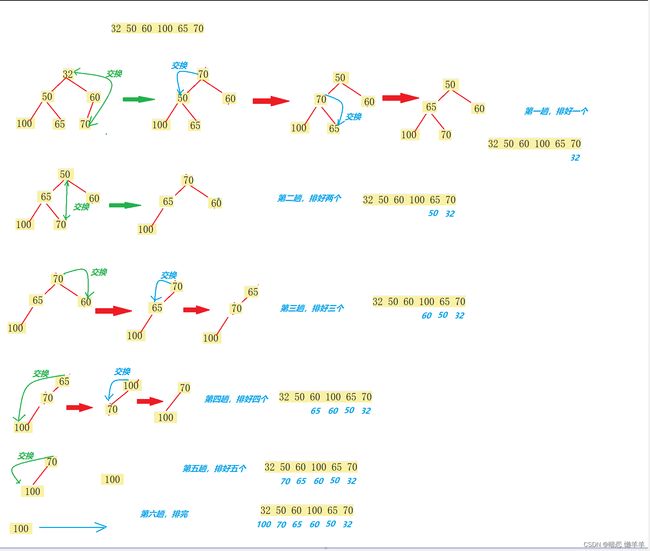
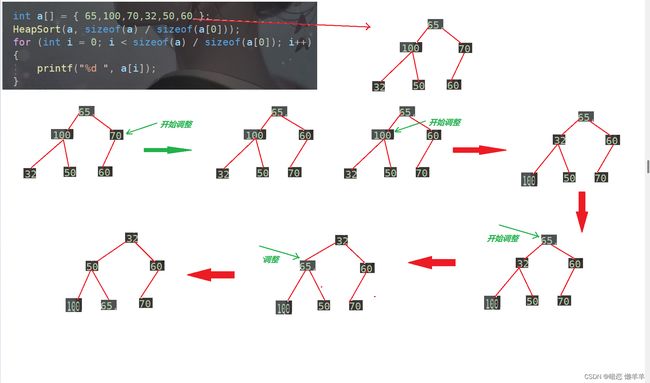
OK,举个排序的例子:
向上调整建堆
void HeapSort(HPDataType* a, int n)
{
//向上调整建堆
//O(N*lgN)
for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}
//向下调整排序
//O(N*lgN)
int end = n - 1;
while (end)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}这里的向上调整建堆和上面堆的插入是一个思路!时间复杂度是O(lgN*N),向下调整排序的时间复杂度是:O(N*lgN)---->有n个元素,每排好一个一下下标,也就是上面的删除的思路!
向下调整建堆
void HeapSort(HPDataType* a, int n)
{
//向下调整建堆
//O(N)
for (int i = (n - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//向下调整排序
//O(N*lgN)
int end = n - 1;
while (end)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}向下调整建堆,就是从倒数第一个元素的父节点开始向下调整为堆!这样越往上层节点的左右子树必定是堆!
OK,测试一下:
没问题~!
复杂度分析
时间复杂度:O(N*logN)
向下调整和向上调整的时间复杂度都是O(logN)即最多调整高度次,但向上调整建堆是O(N*log)而向下调整建堆的O(N)如下图~!删除排序的时间复杂度是O(N*logN),所以综合下来就是O(N*logN)
空间复杂度:O(1)
向下调整建堆时间复杂度推导
向上调整建堆时间复杂度推导
OK,本期分享就到这里,好兄弟,下期交换排序不见不散~!