【算法】二分答案法

引言：

根据二分答案法这个名字我们可以知道，这个算法一定和二分查找有着密不可分的联系。而二分查找是我们较为熟悉的算法了，要你在一个有序数组中判断一个数字是否存在或找到某一个具体的数字，基本上都能想到二分查找

还是以解决问题的形式，形象生动的描绘这个算法的精妙之处。

问题：给你一个数组和一个机器人robert，机器人一开始位于在索引0处，除索引0处的元素外数组中的每一个元素代表一个关卡的能量值，如：energies[1] = 3，代表索引1处的能量值为3；机器人有一个初始能量值，机器人每走到一个索引时，就会得到或者失去能量，规则是：当机器人即将走到索引i处时，如果机器人此时的能量>索引i处的能量值，那么就会得到机器人能量值 - 索引i处的能量值；如果机器人此时的能量<索引i处的能量值，那么就会失去索引i处的能量值 - 机器人能量值，打个比方：机器人一开始在energies[0]处，能量值为2，现在它想要走到energies[1]处，energies[1] = 3，由于索引1处的能量值大于机器人所拥有的能量值，所以机器人失去 3 - 2 = 1个能量值(反之则是得到xx能量)，当机器人走到energies[1]时，其拥有的能力值为1。现在问你：！！！机器人一开始最少需要多少能量才能走到数组末尾(走到数组末尾时，机器人拥有的能力值>=0)

让我们通过三个步骤来思考如何解决这个问题：

1.我们能不能预测一下答案的大致范围(最小值是多少，最大值是多少)？ 当然可以！！ 最小值就是0嘛，因为energies能量数组所有关卡的能量值可能都为0，因此机器人只需要0能力值就可以走到数组末尾；最大值不就是energies数组中的最大值吗？因为机器人能量大于关卡能量的时候是得到能量，小于的时候才会失去，当机器人能量是数组中的最大值时，它会一直获得能量，肯定能走到数组末尾

2.如果一个能量值x能满足题目要求，那么比能力值x大的能量值y可以满足题目要求吗？ 当然可以！！ 机器人的初始能量值越大，那么它通过就越有优势(在关卡能力值比机器人能量值低时可以获得更多能量，或者在关卡能力值比机器人能量值高时失去更少能量)

3.如果一个能量值a不能满足题目要求，那么比能力值a小的能力值b可以满足题目要求吗？ 不可以！！ 因为能力值越小，在过关时，得到的能量会越少，同时失去的能量也会变多，通过会更没有优势

4.我们可以建立一个函数f，在条件限制的情况下，判断一个答案是否满足要求

具体code如下：

(1).先通过一个generate函数生成一个元素值随机的数组，数组长度为n，数组元素值的范围在1-v之间

public static int[] generate(int n,int v){
    int [] ans = new int[n];

    for(int i = 1;i < n;i++)
        ans[i] = (int) ((Math.random() * v) + 1);

    return ans;
}

(2).在0-energies数组最大值这个范围上不断对答案进行二分

int l = 0,r = 0;
for(int energy : energies)
    r = Math.max(r,energy);

int m = 0;
int ans = 0;

while(l <= r){
    m = l + (r - l) / 2;

    if (f(energies,m,r)){
        //答案合法，则可以记录答案
        ans = m;
        //往左侧二分
        r = m - 1;
    }else{
        //答案不合法，不记录答案，往右侧二分
        l = m + 1;
    }
}
return ans;

(3).验证函数f，判断答案是否满足题目要求(这里要传入energies数组中的最大值max，当机器人的能量值>max时，那么它一定能通关)

public static boolean f(int [] energies,int energy,int max){
        for(int i = 1;i < energies.length;i ++){
            if(energies[i] > energy){
                energy -= energies[i] - energy;
            }else{
                energy += energy - energies[i];
            }

            if(energy > max)
                return true;
            //在走到中途时，机器人能力值<0，则说明它无法走到数组末尾
            if(energy < 0)
                return false;
        }

        return true;
}

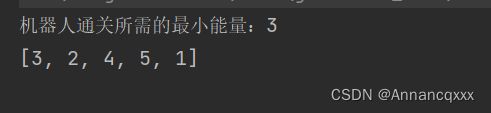
(4).最终结果(索引0处的元素是机器人一开始拥有的能量)：

二分答案法三部曲总结：

1.是否可以预估出答案的大致范围：[最小值，最大值]，在这个范围上不断二分

2.答案是否存在单调性：一个答案x满足题目要求，那么比它大的所有答案也满足题目要求；一个答案y不满足题目要求，那么比它小的所有答案也不满足题目要求

3.建立一个验证函数f()，在条件限制的情况下，判断答案是否满足题目要求

关于这道题的一个小优化点：

为什么验证函数f要传入一个max值，并在机器人在大于这个max值后就可以退出判断？

1.比如：[2,2,2,2,2,2,3]这是能量数组，假设机器人能力值为3，那么机器人在走的过程中会不断获得能量，并且每次获得的能量会比前一次的更多，呈指数级，如果数组长度很大，那么机器人在走的过程中不断获得能量会有整型溢出的风险

2.在机器人能量>=max值时，不管怎样，它都是获得能量，或者能量不变，一定能走到数组末尾