CGAL的代数基础

         这一节并不影响使用，

1、介绍

        CGAL库的目标是实现非线性对象的精确计算，特别是代数曲线和曲面上的对象。因此，表示多项式、代数扩展和有限域的类型在相关实现中起着更重要的作用。引入此包是为了跟上这些变化。由于引入的框架必须支持多项式，因此该包避免了术语数字类型。相反，该包区分了类型的代数结构以及类型是否可嵌入实轴或可嵌入实数。此外，该包引入了可互操作类型的概念，允许显式处理混合操作。

2、代数结构

        本节介绍的代数结构概念是受传统代数中众所周知的对应概念的启发，但我们也不得不考虑现有类型及其限制。为了保持接口最小化，我们不希望涵盖所有已知的代数结构，例如，我们没有为诸如群或例外结构（如斜场）等基本结构引入概念。

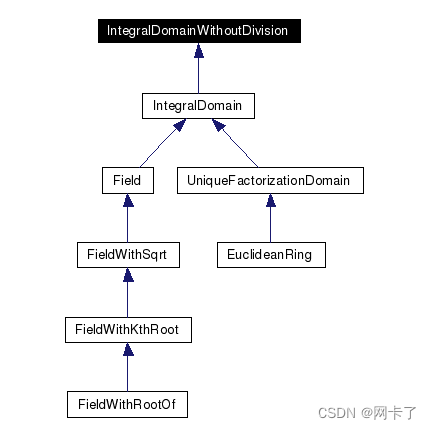
        上图显示了代数结构概念的细化关系。IntegralDomain、UniqueFactorizationDomain、EuclideanRing和Field对应于同名代数结构。FieldWithSqrt、FieldWithKthRoot和FieldWithRootOf分别是分别在“sqrt”、“k次根”和“多项式的实根”运算下闭合的域。概念IntegralDomainWithoutDivision也对应于代数意义上的整环，其区别在于一些整环的实现缺乏（代数上总是定义良好的）整数除法。请注意，Field细化IntegralDomain。这是因为大多数环论概念，如最大公约数，对于Fields来说变得微不足道。因此，我们将Field视为IntegralDomain的细化，而不是更高级的环概念的细化。如果一个算法想要依赖gcd或余数计算，它首先会试图在Field中做一些不应该做的事情。 

2.1、代数范畴

        对于AS类型，Algebraic_structure_traits提供了几个标签。最重要的标签是

        Algebraic_category标签，它表示AS类型满足的最精细的代数概念。该标签是以下标签之一：        

        Integral_domain_without_division_tag、

        Integral_domain_tag、

        Field_tag、

        Field_with_sqrt_tag、

        Field_with_kth_root_tag、

        Field_with_root_of_tag、

        Unique_factorization_domain_tag、

        Euclidean_ring_tag。

        这些标签彼此衍生，以反映代数结构概念的层次结构，例如，Field_with_sqrt_tag衍生自Field_tag。

2.2、精确和数值敏感

        此外，Algebraic_structure_traits提供了标签Is_exact和Is_numerical_sensitive，它们都是Boolean_tags。

        如果一个代数结构的概念所要求的所有运算都是计算出来的，并且两个代数表达式的比较总是正确的，那么这个代数结构就被认为是精确的。

        如果类型的性能对算法的条件数敏感，则认为代数结构对数值敏感。

3、实数嵌入

        大多数数字类型表示实数的某个子集。从这些类型中，我们期望能够计算符号、绝对值或双精度近似值的功能。特别是，我们可以期望这种类型上存在一个顺序，它可以反映实数轴上的顺序。所有这些属性都聚集在RealEmbeddable概念中。该概念与代数结构概念正交，即只表示实数轴上的值的类型也可能成为RealEmbeddable的模型，因为它不提供任何算术运算。

4、实数类型

        每个CGAL内核都带有两种实数类型（可嵌入实数的数字类型）。其中一种是FieldNumberType，另一种是RingNumberType。基本内核对象（点、向量等）的坐标来自这些类型之一（笛卡尔内核为FieldNumberType，齐次内核为RingNumberType）。

        FieldNumberType概念结合了Field和RealEmbeddable概念的要求，而RingNumberType概念结合了IntegralDomainWithoutDivision和RealEmbeddable。从代数上讲，实数类型没有形成不同的结构，因此没有列在上图的概念层次结构中。

5、转换

        本节介绍了类型的互操作性的两个概念，即ImplicitInteroperable和ExplicitInteroperable。虽然ExplicitInteroperable是基本概念，但我们首先从ImplicitInteroperable开始，因为它更直观。

        一般来说，混合操作是由重载运算符和函数提供的，或者只是通过隐式构造函数调用提供的。这种级别的互操作性由概念“ImplicitInteroperable”反映出来。然而，在模板代码中，混合算术运算的结果类型，或所谓的强制类型，可能不明确。因此，该包引入了Coercion_traits，通过Coercion_traits::Type访问两个互操作类型A和B的强制类型。

        一些简单的例子是 int 和 double 的强制类型 double，或者 Gmpz 和 Gmpq 的强制类型 Gmpq。但是，强制类型不一定是输入类型之一，例如，整数系数多项式乘以有理类型的强制类型应该是有理系数多项式。

        强制转换特性还需要提供一个函数Coercion_traits::Cast()，将输入类型转换为强制转换类型。这实际上是更基本的概念ExplicitInteroperable的核心。引入ExplicitInteroperable是为了涵盖更复杂的情况，在这些情况下，很难或不可能保证隐式互操作性。请注意，这个函数对ImplicitInteroperable类型也有用，因为它可以用来消除冗余的类型转换。

6、分数

        除了需要对对象进行整体代数运算外，还有一些数字类型，人们希望将其分解为分子和分母。一个类型是Fraction，则Fraction_traits提供了相关功能以及分子和分母类型。特别是Fraction_traits提供了一个标签Is_fraction，可用于分派。

        一个相关的类是 Rational_traits，它出于向后兼容的原因而保留。但是，我们建议使用 Fraction_traits，因为它更通用，并提供调度功能。