【论文阅读】Subgraph Matching with Effective Matching Order and Indexing

Sun S, Luo Q. Subgraph matching with effective matching order and indexing[J]. IEEE Transactions on Knowledge and Data Engineering, 2020, 34(1): 491-505.

Abstract

子图匹配可以从数据图中找到与查询图相同的所有嵌入。最近的算法可以通过基于查询图在数据图上生成树结构索引，将树中的顶点从根到叶的路径排序，并按照匹配的顺序枚举嵌入。然而，我们发现这种基于路径的排序和基于树结构索引的枚举固有地限制了性能，因为缺乏对跨树路径的顶点之间的边的考虑。为了解决这个问题，我们提出了一种基于代价模型生成匹配顺序的方法，同时考虑查询顶点之间的边和候选匹配点的数量。此外，我们为数据图中的候选顶点及其选择的邻居创建一个二部图索引，并使用该索引按照匹配的顺序执行枚举。我们在真实世界和合成数据集上的实验表明，我们的方法比现有的技术要优越了一个数量级。

1 INTRODUCTION

给定一个图q作为查询，另一个图G，通常远远大于q，作为数据图，子图匹配找到G中与q同构的所有嵌入。例如，给定q和G在图1、{（u0、v0）、（u1、v1）、（u2、v3）、（u3、v6）}为匹配项。

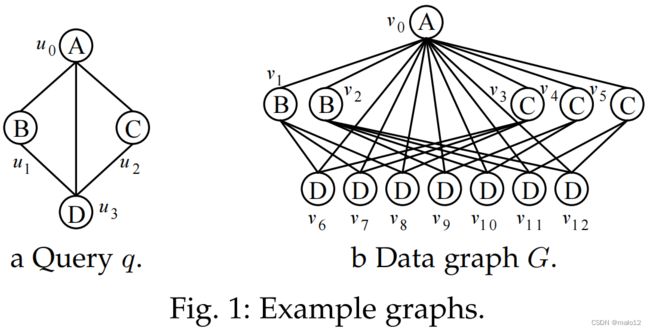
子图匹配问题是np完备[6]，并提出了多种算法[3]、[5]、[9]、[11]、[20]、[23]、[28]。这些算法侧重于生成有效的匹配顺序并设计强大的过滤策略来最小化数据图中候选对象的数量。QuickSI [23]设计了不常见边优先排序技术，它对查询的边缘进行排序图在数据图中按频率的升序排列。GraphQL [11]采用左深连接排序策略，将枚举过程建模为连接过程。SPath [28]、TurboIso [9]和CFL [3]提出了基于路径的排序方法，该方法通过将查询图分解为多个路径，并根据对路径进行排序来生成匹配的顺序估计的每个路径的嵌入数。除了排序策略外，最先进的算法，如TurboIso [9]和CFL [3]，采用了一个基于树的框架，构建一个轻量级的树结构索引来最小化候选的数量，并基于索引而不是原始数据图来枚举所有的匹配。尽管这些技术都有显著的优点，我们还是在其中发现了一些固有的问题。
首先，现有的排序策略只考虑每个顶点（或路径）的候选数量，但忽略了查询顶点之间的边。
例1.1 给定在图1中的q和G，现有的排序策略，包含了不频繁边优先顺序，左深连接优先和基于路径排序，包含匹配顺序PI= (u0, u1, u2, u3)基于数据图的候选数量：u0.C={v0},u1.C={v1-2},u2.C={v3-5},u3.C={v6-12}。在枚举期间，u1，u2，和u3包含他们基于u0的候选数据。图2展示了递归枚举过程，解释了一个根据匹配顺序的映射数据节点到查询节点的部分结果。每个节点si（i=0，…，9）表示部分结果，例如s2：{(u0,v0),(u1,v1)}，一个边对应于查询顶点和数据顶点之间的映射，例如e(s1,s2):(u1,v1)。在这个匹配的顺序中，总共42个嵌入中的35个在枚举结束时才被排除。相比之下，如果我们将u2和u3的匹配顺序交换，(u0, u1, u3, u2)，我们可以在早期阶段修剪无效的中间结果，因为在q中在u1和u3之间有一条边。

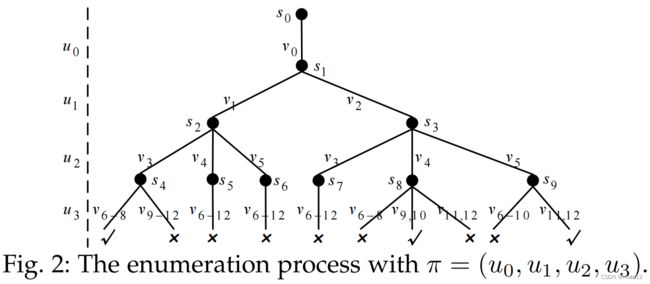
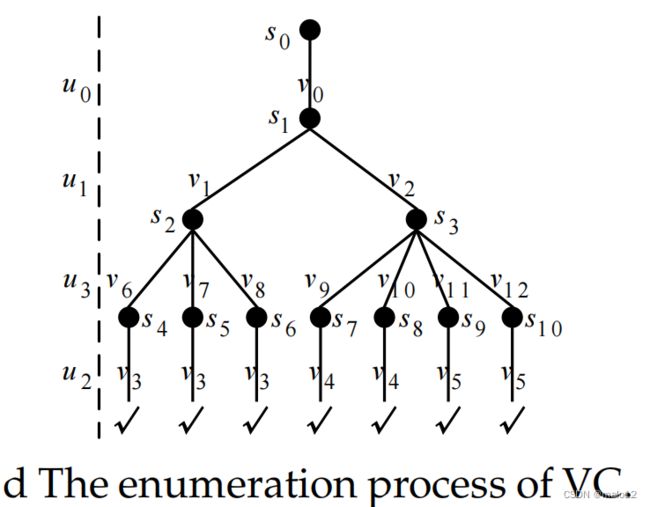
此外，如果u2和u3分别根据u3和u1而不是u0得到它们的候选对象，则可以进一步减少搜索空间。图5d显示了使用这两个改进的枚举过程这比图2中的效率要高得多。

其次，在基于树的框架中，匹配顺序由树结构索引[3]，[9]生成，它只维护路径上的边。因此，即使有一个更有效的顺序，索引也不能支持枚举。换句话说，基于树的框架本质上限制了匹配顺序的生成。
例1.2 对于图3a中的q和图1b中的G，qt是一个植根于u0（用粗线表示）的BFS（宽度优先搜索）树。图3b中的树状结构索引Gt具有相同的结构作为qt，并存储每个查询顶点的候选集以及原始数据图中候选集之间的边。Gt不能支持沿着（u0、u1、u3、u2）的枚举，因为它不支持保持u1.C和u3.C之间的边缘。

此外，我们发现现有的工作可以受益于更强的过滤策略，以最小化候选集的大小，因为它们既可以进一步降低部分结果的搜索广度，又可以为匹配顺序的生成提供更准确的统计数据。
我们的方法。基于这些观察结果，我们提出了一种新的子图匹配算法VC（顶点连通性）。不同于基于树的框架，它首先构造索引和n根据索引生成匹配顺序，VC对一个新进程进行子图匹配，该进程包括四个步骤：
(1)为每个查询顶点提取一个候选集；
(2)根据候选集的统计数据生成匹配顺序；
(3)构造一个二部图索引BI，存储数据节点之间的边；
(4)枚举基于BI的所有结果。前三个步骤分别是索引阶段和最后一个步骤是枚举阶段。
在候选提取过程中，VC首先生成一个候选集u。C为每个查询顶点u沿着一个查询顶点的顺序，称为索引顺序。
然后，VC利用伪星同构约束和乒乓滤波策略，按照索引顺序对候选集进行细化。接下来，VC使用基于顶点的排序策略生成一个查询顶点的顺序，称为匹配顺序，该策略同时考虑了候选集的大小和查询节点之间的顶点连通性。在生成匹配的顺序时，VC还获得了一个枢轴字典，这是一组查询顶点对，用于确定要存储在索引中的数据图中的边。在那之后，我们进一步构造一个大图（即二部图）索引BI：对于枢轴字典中的每一对顶点的索引BI（u，u‘），我们检索候选集u.C和u’.C作为两组顶点，并在数据图中显示的这两个集合之间添加边。最后，我们通过沿着BI协助的匹配顺序递归地扩展部分结果来枚举所有匹配。
VC通过同时考虑候选集的大小和查询顶点之间的边来生成匹配的顺序，这解决了现有的排序策略只考虑候选的数量。通过重新设计执行子图匹配的过程并提出二部图索引，我们打破了在基于树的框架中对匹配阶数生成的约束，因为边在VC的二部图索引中维护依赖于支点字典，这是在生成匹配顺序时得到的，而在基于树的框架中生成的匹配顺序依赖于树结构索引。此外，基于伪星同构约束和乒乓滤波策略对候选集进行细化，可以进一步最小化候选集的大小。
贡献。综上所述，本文有以下贡献。
我们提出了一种新的子图匹配算法VC，它与现有的子图匹配算法不同。
我们用一个伪星同构约束和一个乒乓过滤策略来最小化查询顶点的候选集。
我们使用基于顶点的排序策略生成一个匹配的顺序，该策略同时考虑了候选的数量和查询顶点之间的边。
我们设计了一个用于枚举的二部图索引，其空间复杂度为O（|E (G)|×|V (q)|），构造的时间复杂度为O（|E (G)|×|E (q)|）。
最后，我们将VC与各种现有的在真实和合成数据集上具有不同排序策略的算法进行比较，并使用最新性能研究[13]的新实验指标。研究结果表明，VC算法明显优于以往的算法。
论文组织。第2节介绍了背景知识。第3节概述了我们的VC算法。第4和5节介绍了指数的构建和匹配顺序的生成。我们在第6节中评估VC，并在第7节中得出结论。

2 BACKGROUND

2.1 Preliminaries

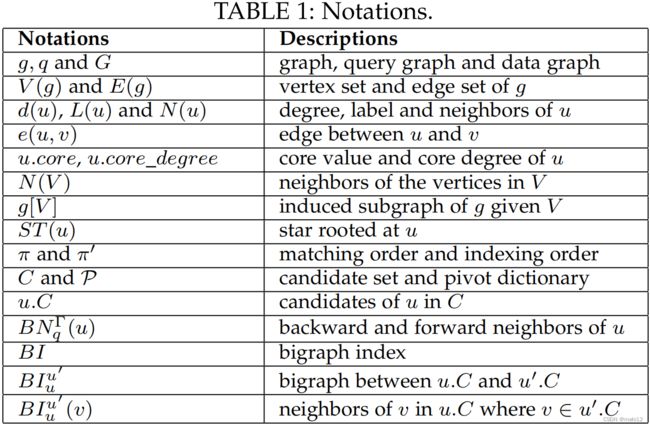
在本文中，我们关注顶点标签的无向图g =（V，E，Σ，L），其中V是一组顶点，E是一组边，Σ是一组标签，L是一个关联一个顶点的函数v与标签L (v)∈Σ。查询图q是连接的。接下来，我们给出了子图匹配的正式定义和相关的初步定义，表1对常用的符号进行了总结。

定义1。子图同构（Match）：给定一个查询图q =（V，E，Σ，L）和一个数据图G =（V 0，E0，Σ 0，L0），一个子图同构（Match）是一个内射函数f： V→V0满足条件：
(1).∀u ∈ V, L (u) = L 0 (f (u));
(2).∀e (u, v) ∈ E, ∃e (f(u), f (v)) ∈ E‘
为了简单起见，我们称子图同构为匹配。
定义2。子图匹配：给定q和G，找到从q到G的所有匹配项。
定义3。顶点诱导子图：给定一个图g =（V，E，Σ，L）和V’⊆V，在V‘上构造的g的顶点诱导子图表示为g[V‘] =（V’，E‘，Σ，L），其中E’={e（u，|）|e(u，v)∈E和u，v∈V‘ }。
定义4。星：给定一个图g和一个顶点u∈V (g)，一个根为u的星，记为ST (u)，是根为u的深度1的树，它包含g中u的所有邻居顶点。
定义5。顶点的顺序：给定一个查询图q，一个阶Γ是q中的顶点的排列。Γ[i]是Γ中的第四个顶点，而Γ[i： j]是Γ中从索引i到j的顶点的集合。我们就可以了ll一个用于匹配匹配顺序的顶点顺序，记为π，一个用于索引索引顺序，记为π‘。
定义6。连接顺序：给定一个查询图q和一个顺序Γ，如果给定任意1 6 i 6 |Γ|，则Γ连通，则顶点诱导子图q[Γ[1： i]]连接。
定义7。向后邻居：给定一个查询图q，一个阶Γ和一个顶点u = Γ[i]，u的向后邻居，记为BNq Γ(u)，是u在Γ中位于u之前的邻居。
定义8。完整的候选集：给定q和G，一个候选集u。C对于u，∈V (q)是完整的，如果u。C满足：如果一个映射（u，v）存在于从q到G的任何匹配中，其中v∈∈(G)，那么v∈u。C. 如果是∀u∈V (q)，则是u。C是完备的，那么我们说C是完备的。
定义9。轴和轴字典：给定一个查询图q和一个连接匹配顺序π，查询顶点u的轴是BNq π (u)中的一个查询顶点u0。枢轴字典，记为P，记录每个查询顶点的轴，P[u]表示u的轴。π[1]没有轴，因为它没有向后的邻居。
核的概念首先是由塞德曼提出的，它测量了一个图[22]的局部密度。k核的定义如下。
定义10。k核：给定一个图g，g的k核是g的极大连通子图g‘，满足∀u∈V（g’），d (u) > k，其中d (u)是u在g‘中的度。
定义11。核值：给定一个图g和一个顶点u∈V (g)，u的核心值，记为u.core，如果u属于∈核但不是任何（c+1）核。
Batagelj[2]等人提出了一种O（|E (g)|）算法来计算g中所有顶点的核心值，并证明了在一个连通图中恰好存在一个2核。我们使用这个算法来计算u.core。CFL [3]的核心结构定义如下。
定义12岁的人。核心结构：给定一个查询图q，q的核心结构是q的2核结构。
我们在定义13中进一步定义了核心度。在生成索引顺序和匹配顺序时，我们根据顶点的核心值和核心度对顶点进行优先排序，以排除影响不在核心结构中的顶点。
定义13岁。核心度：给定一个查询图q，设VC为q的核心结构中的顶点集。u的核心度为|N (u)∩VC |，记为u.核心度。如果是一个顶点u/∈VC，u.core degree为0。

2.2 Related Work

为了将我们的研究放在上下文中，我们根据所解决的问题对相关的工作进行了分类：标签子图匹配和无标签子图匹配。本文的重点是标签子图的匹配问题。
标签子图匹配。标签子图匹配的目的是在单个标签的数据图中找到所有匹配。根据搜索过程的执行阶段，我们将算法分为直接算法-枚举和索引计算。直接枚举方法，如Ullmann [26]、VF2 [5]、QuickSI [23]、GraphQL [11]和SPath [28]，之前没有构造给定查询图的索引枚举，但根据邻域签名[28]等过滤器分别获得每个查询顶点的候选项。由于缺乏准确的信息来估计成本，该匹配顺序可能是无效的，可能有许多假阳性候选。Lee等人[18]对这些算法进行了广泛的讨论，并表明这些算法在其中存在问题匹配顺序选择和基于签名的滤波器只对某些数据集有效。
为了解决直接枚举算法中的问题，研究人员提出将搜索过程分为两个阶段，第一个阶段构造给定查询图的索引，第二个阶段基于索引的ucts枚举。该指标不仅减少了候选对象的数量，而且提供了准确的成本估计，以生成有效的匹配顺序。TurboIso [9]设计了一个tree结构化索引、候选区域，并通过基于路径的排序策略生成匹配顺序。此外，TurboIso [9]提出了邻域等价类来压缩查询图中相似节点。CFL [3]是一种最先进的算法，通过以核心结构中的优先排序笛卡尔顶点来加速枚举，并提出了一个新的树状结构指数CPI，降低了从TurboIso的O（|V (G)| |V (q)|）到O（|E (G)|×|V (q)|）的空间复杂度。TurboIso和CFL都在直接枚举算法取得了令人印象深刻的加速。
此外，以往的研究通过利用数据图中的顶点关系 [20]，改进了标记子图的匹配，利用多个查询[21]之间的计算结果，并在单台机器[13]、[15]或分布式环境[25]上并行化算法。
无标签的子图匹配。无标签子图匹配是在无标签图中找到所有匹配。由于缺乏标签，无标签的子图匹配比有标签的子图匹配更具挑战性。此外，还需要无标记子图匹配来处理自同构，以消除匹配结果[7]中的任何重复。对这一问题的最新研究主要集中在设计并行上诸如Afrati [1], TwinTwig [16], SEED[17], PSgL [24], Crystal [19] and DualSim [14]。

2.3 Tree-based Frameworks

最新的子图匹配算法CFL [3]和TurboIso [9]采用了一个基于树的框架来进行子图匹配。在下面，我们使用最先进的算法CFL作为一个代表来说明基于树的框架的一般思想。
给定q和G，CFL首先通过选择一个根顶点u并从u中进行BFS遍历，从q中得到一个BFS（宽度优先搜索）树qt。接下来，CFL在G上基于qt构造了一个树状结构的索引CPI。具体来说，CPI沿着qt的自顶向下顺序为每个查询顶点生成一个完整的候选集。在生成过程中，CPI在每个级别上进行向后修剪。在生成之后，CPI沿着qt逐级执行自下而上的细化，以最小化候选集的大小。生成和细化都是基于以下观察结果：给定v∈u。C，如果（u，v）存在于从q到G的匹配中，则∀u‘∈N (u)，N (v)
∩u‘.C = ∅.此外，在生成和细化过程中，CPI不仅维护候选顶点还存储了候选顶点之间的边。CPI构建后，CFL采用基于路径的排序策略生成匹配的顺序。特别是，CFL根据中每个路径的估计嵌入数对qt的路径进行排序CPI。最后，CFL根据CPI沿着匹配顺序枚举所有匹配项。
例子2.1。给定图1中的q和G，CFL得到了基于u0的BFS树qt，如图4a所示。接下来，CFL构造了图4b中的树状结构索引CPI，它具有相同的结构as qt.CPI存储每个查询顶点的候选集以及原始数据图中候选顶点之间的边。qt包含三条路径，分别是p1 =（u0、u1）、p2 =（u0、u2）和p3 = (u0、u3).CFL根据CPI中嵌入的数量对这三条路径进行排序，即（p1、p2、p3）。因此，CFL得到了匹配的顺序π =（u0、u1、u2、u3）。最后，CFL在CPI的帮助下枚举了π中的所有匹配项，这与图2中的枚举过程相同。

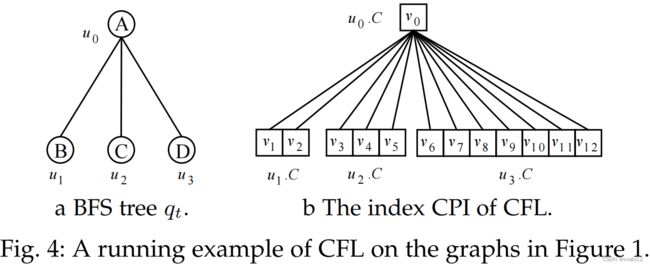
与基于树的框架相比，VC有四个区别： (1) VC重新设计了执行子图匹配的过程；(2) VC将候选对象的提取简化为前向和向后的利用较强的剪枝策略对候选集进行标记和细化；(3) VC采用基于顶点的排序方法，而不是基于路径的排序方法；(4) VC将索引建模为在候选集合之间的多个二部图。

3 ALGORITHM OVERVIEW

给定q和G，VC通过将沿着匹配顺序的查询顶点映射到候选顶点，递归地扩展部分结果。因此，VC需要一个完整的候选集C和一个匹配的顺序π。此外，我们构造了两个辅助结构，一个枢轴字典P和一个二部图索引BI，以加速枚举的速度。
当通过将查询顶点u映射到数据顶点v来扩展部分结果时，我们只需要考虑数据顶点，它们是数据顶点的邻居，并且属于候选集u。C根据定义1和定义8。因此，我们选择u的一个后向邻居u‘来保持u‘之间的关系。u’.C和u.C来方便枚举。u的后邻居u0是u的轴，轴字典P记录除了π[1]之外的每个查询顶点的轴，因为π[1]没有后邻居。我们为p中的每一对顶点构造包含二部图索引BI。BI中的二部图有两个顶点集u.C和u’.C其中，（u，u’）是P中的一对顶点，u’是u的pivot。u.C和u’.C之间的二部图记为BIu‘u。

算法1给出了我们的VC算法，它以q和G作为输入，并输出从q到G的所有匹配。我们首先提取每个查询顶点的候选对象（第2行）。接下来，我们生成匹配调整顺序π和枢轴字典P（第3行）。第4行构造了二部图索引BI。我们将这三个步骤称为索引阶段。
在索引阶段之后，枚举阶段沿着基于BI的π逐点递归地扩展部分结果。如果所有查询顶点都被映射，我们输出结果并return（第11行）。否则，我们将得到π中的下一个查询顶点u和u的枢轴（第12行）。我们通过将一个候选项映射到u（第13-15行）来扩展部分结果M。我们根据BIu‘u得到了u的候选者和数据顶点映射到u的轴心（即，BIu‘u（M[u 0 ]）)。对于u的候选v，第14行检查v是否匹配，并有映射到后邻居的数据顶点的边。如果是这样，我们将递归地调用枚举。验证函数不检查v和映射到u的数据顶点之间的边缘，因为v来自BIu‘u (M[p])，所以边缘就存在了。在枚举期间，原始数据图仅用于检查数据顶点之间是否存在边（第18行）。
例子3.1。图5显示了在图1中的图上运行的VC算法。候选提取的结果如图5a所示。每个候选人设置u。C存储其中的数据顶点可以映射到u。图5b显示了由VC生成的匹配顺序和枢轴字典。以u3为例：
BNq π（u3）= {u0，u1}和u1被选为其枢轴。在匹配的顺序中，起始顶点u0没有枢轴。对于P中的每一对顶点（u，u0），我们构造一个大曲线图来保持相对性nship之间。C和u0。C,如图5c所示。具体来说，BIu u 0维护了u中数据顶点之间的边。C和u0。C在原始数据图中。以u0.C中的v0和u1.C中的v1为例： e（v0，v1）存在于E (G)中，那么就有一个在BIu0 u1中，在v0和v1之间的边。此外，在BIu0 u1中，BIu0 u1（v0）= {v1，v2}。最后，基于BI的沿π的枚举过程如图5d所示。

4 BIGRAPH INDEX

在本节中，我们提出了一个二部图索引BI，它分候选提取和索引构建。

4.1 Candidate Extraction

给定q和G，候选提取是为每个查询顶点获得一个完整的候选集。为了生成一个尽可能小的完整的候选集，我们定义了精确的星同构常数绘制并标识匹配下的一对查询和数据顶点之间的属性。
定义14 精确星同构约束（ESIC）：给定q和G，C是由LDF构造的完整候选集。给定u∈V (q)和v∈V (G)，（u，v）满足精确的星形同构约束，如果存在一个从ST (u)到ST (v)的匹配f，使∀u 0∈N (u)，f（u 0）∈u0。C.
引理4.1 给定q，G，u∈V (q)和v∈V (G)，如果一个映射（u，v）存在于一个从q到G的匹配中，那么（u，v）满足精确的星形同构约束。
基于引理4.1，给出了u∈V (q)和v∈u.C，v可以从u.C中删除。如果（u，v）不满足ESIC，则C不破坏其完整性。我们使用在近似子图中提出的一种技术是单同态算法[10]检验（u，v）是否满足ESIC： (1)构造一个大图，表示为Buv，以N (u)和N (v)为双分区，其中在u’∈N (u)和v’∈N (v)之间加一条边if v’∈ u’.C. 我们称该方法为邻域二部图构造；(2)执行最大二部图匹配[27]来检验Buv(即半完美匹配的存在性，每个顶点在N(u)中匹配）。
例子4.1。根据图6a和图6b中的q，LDF构造的完整候选集C如下： u0.C = {v0}，u1.C={v1−2}，u2.C = u3.C = {v3}，u4.C={v3−5}和u5.C = u6.C = {v6−7}.ST（u0）和ST（v0）分别在虚线矩形中。如图6c所示，Bu0 v0是使用邻域二部图构造方法构造的二部图。因为Bu0 v0没有半完美匹配，（u0，v0）违反了ESIC。然后，v0可以安全地从u0.C中移除。

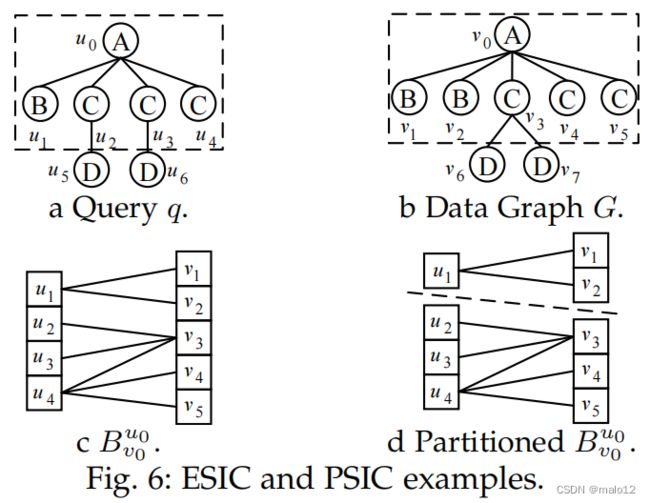
构造Buv的时间复杂度为O（d(u)×d (v)）。最大大曲线匹配的时间复杂度记为Φ（d (u)，d(u)，d(v)）(例如，O（n 2.5），其中n是Buv中节点的数量）。然后，检查每个查询顶点及其候选顶点的时间复杂度为O(Pu∈V(q)Pv∈V(G)（d(u)×d (v) + Φ（d (u)，d(v)））=O(|E(q)|×|E(G)|+Pu∈V(q)Pv∈V(G)Φ（d(u)，d(v)）。就因为是这个，检查很昂贵，我们提出了一个问题：
我们是否可以删除最大大匹配检查，同时保持ESIC的竞争性过滤能力？
为了回答这个问题，我们首先定义邻域标签等价类如下。
定义15 邻域标签等价类：给定一个图g和一个顶点u∈V (g)，u的邻域标签集包含其邻域顶点的所有不同标签，记为NLS (u)。G对于NLS (u)，邻域标签等效类NLEC（u，l）是{u‘|u’∈N (u)和L（u‘）= l}。
例子4.2 给定图6a中的u0，NLS（u0）= {B、C}、NLEC（u0、B）= {u1}和NLEC（u0、C）= {u2、u3、u4}。
其次，为了消除最大大匹配检验，定义了伪星同构约束，并证明了定理4.1。
定义16 伪星同构约束（PSIC）：给定q和G，C是由LDF构造的完整候选集。给定u∈V (q)和v∈V (G)，（u，v）满足伪星同构构体m约束，如果∀l∈NLS (u)，X = Θ[1： i]，其中Θ是NLEC（u，l）和1 6 i 6 |Θ|的顶点排列，以下两个条件成立： (1) ∀u 0∈X，u’.C∩N (v) =∅；和(2) |X| 6 |∪u’∈X(N(v) ∩ u’.C)|.
定理4.1 给定q，G，u∈V (q)和v∈V (G)，如果一个映射（u，v）存在于一个从q到G的匹配中，则（u，v）满足伪恒星同构约束。
证明：给定q和G，由LDF构造的C是完整的。假设（u，v）存在于从q到G的匹配中，其中u∈V (q)和v∈V (G)。然后，（u，v）满足ESIC（引理4.1)。因此，存在一个利用邻域双曲线图构造方法构造Bv u中的半完美匹配。根据Hall定理[8]，∀Y⊆N (u)，|Y|6|(Y)|N在Buv。给定N (u)中的u’和u’，其中L（u’）= L（u’’），Bv u的构造方法保证了u’和u ’’在Buv中没有共同的邻居，因为u’.C ∩ u’.C = ∅.所以，∀Y⊆NLEC（u，l）其中l∈NLS (u)，|Y | 6 |N（Y）|。由于Bv u有一个半完美的匹配，∀u’∈Y，u’.C ∩ N (v) = ∅.因为Bv u中的N (Y)与∪u’∈Y(N(v)∩u’是相同的。C)是基于社区的大说唱音乐h构造方法，|Y | 6 |∪u’∈Y(N(v)∩u’.C)|.因此，给定X = Θ[1： i]，其中Θ是NLEC（u，l）和1 6 i 6 |Θ|中顶点的任何排列，∀u’∈X，u’.C∩N (v) =∅和|X| 6 |∪u’∈X (N(v)∩u’.C)|.因此，这个定理就成立了。
基于此定理，给出了u∈V (q)和v∈u。C，我们可以安全地排除v。C，如果（u，v）不满足PSIC。PSIC分别检查每个NLEC（u，l），而不是N (u)，因为它可以改进滤波功率。我们使用下面的例子来说明它。
例子4.3。在图6c中，如果我们用N（u0）和N（u0）=（u1，u2，u3，u4）检查PSIC，那么（u0，v0）满足PSIC。相比之下，如果我们分别用NLEC（u0，B）和NLEC（u0，C）来检查PSIC，如图6d和Θ（NLEC（u0，C））=（u2，u3，u4），那么（u0，v0）不满足PSIC，因为|{u2，u3}| < |N（{u2，u3}）|。但是，如果Θ（NLEC（u0，C））=（u4，u3，u2），则（u0，v0）满足PSIC。
NLEC（u，l）中顶点的排列可能会影响PSIC的过滤效果。然而，我们的实验结果表明，一个顶点的随机顺序足以使PSIC实现作为ESIC的竞争性过滤能力。此外，在NLEC中对顶点进行排序也会引入额外的成本。因此，本文在NLEC（u，l）中采用了一个随机的顶点顺序。接下来，我们将呈现我们基于定理4.1开发的候选提取算法。

提取候选对象。算法2概述了候选算法提取的过程。我们首先生成一个查询顶点的连接顺序（第2行）。为了区别于匹配的顺序，我们将其命名为ord其中，我们提取候选序列作为索引顺序，记为π0。我们不是基于LDF的简单构造方法，而是基于CFL观测的正向阶段：给定a查询顶点u，u。C可以得到N (u 0。C)表示所有的u0∈N (u)，其中交点中的顶点与u [3]具有相同的标签。第4-6行得到开始ve的候选集合π0中的rtex，其中包含匹配LDF和邻域标签频率（NLF）过滤器的数据顶点。NLF滤波器是否检查数据顶点的邻居的标签频率大于或等于查询顶点[3]，[9]。接下来，我们开始了前进的阶段π0（第7-11行）。在前进阶段之后，后退阶段根据定理4.1（第12-23行），以π0的相反顺序过滤候选集。乒乓过滤策略立即恢复是更新u后每个u0∈N (u)的候选集。C（第21-23行）。根据定理4.1，以下命题成立。
命题4.1节。给定q和G，由算法2得到的候选集C是完整的。
示例4.4。图7说明了算法2在图7a中的q和图7b中的G上运行。π0是（u0、u3、u1、u2）。我们首先得到u0。C={v0，v1，v4，v6，v8}。接下来，我们沿着π开始了前进的阶段0，并生成u3。基于u0.C的C={v0、v1、v4、v6、v8}。作为BNq π 0（u1）= {u0，u3}，我们从N（u0.C）和N（u3.C）的交点得到了u1.C = {v3，v7}。同样，我们得到了u2。C={v2，v5，v9}.前进阶段的结果如图7c所示。
我们按照π0的相反顺序开始向后阶段。v2从u2.C中移除，因为它在u0.C和u3.C中只有一个不同的邻居。通过乒乓滤波策略，v0为r由于v0在u2.C中没有邻居。类似地，v3被从u1.C中移除。根据更新后的u1.C，v4和v6从u0.C和u3.C中删除。接下来，u3。c没有ch基于乒乓滤波策略，从u2.C中删除了v5。u0。c没有变化。最终结果如图7d所示。

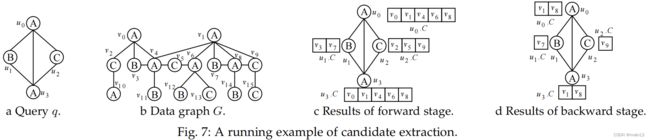
生成索引顺序。我们首先证明了下面的定理。
定理4.2。给定任何连接顺序，不在核心结构中的查询顶点最多有一个后邻居。
证明：给定q，所有不在核心结构中的查询顶点形成一个森林，其中每个顶点都有一个父节点。因此，给定任何连通的顺序，不在核心结构中的顶点结构最多有一个落后的邻居。
因为我们生成u.C基于u在正向阶段的后邻，我们根据后邻的数量对顶点进行优先排序，以在早期sta筛选假阳性候选ge。因此，在生成索引顺序时，我们根据定理4.2，将查询顶点放在不进行查询的核心结构顶点之前。特别地，我们选择了具有最大核心的顶点值作为索引顺序中的起始顶点，而不是具有最大度的起始顶点，以便(1)排除不在核心结构中的查询顶点的影响；以及(2)启动候选对象从核心结构的致密部分中提取。算法3给出了生成索引顺序的细节。

绑扎处理。当最大函数（第3行和第8行）有关联时，我们选择顶点的顺序为：(1) u.core；(2) u.core度；和(3) d (u)引导候选提取到密集的part的q。如果仍然有联系，我们选择具有较低id的顶点。
例子4.5。图7a中给出的q，每个u∈V (q)的u核=2。根据捆绑处理，选择u0作为起始顶点，其核心度为3，id低于u3。在算法3的结尾，我们得到π 0 =（u0、u3、u1、u2）。
由于q作为一个连通图的核心结构是连通的，因此算法3具有以下性质
命题第4.2节。将算法3生成的索引顺序π0连接起来，并将核心结构中的查询顶点定位在π0中的其他顶点之前。

4.2 Index Construction

在生成一个匹配的顺序和一个枢轴字典（第5.2节）之后，我们在这些候选集上构建一个索引，以服务于后续的枚举。在枚举中，我们需要得到候选人一个查询顶点u的轴心u’的s（算法1中的第13行）。为了促进这一步骤，我们保持边缘在u.C和u’.C表示每一对（u，u’）∈P作为一个二部图，表示为BIu’u，与u.C和u’.C作为两个双分区。因为我们从u’中得到了u的候选者，所以BIu’u记录了在u’.C中的候选在u.C中的邻居。索引构建的细节见算法4。

算法4具有以下性质。
命题第4.3节。由算法4构造的BI中的每个二部图BIu’u都满足∀v∈u.C∩N（v’），其中v’∈u’.C, v ∈ BIu’u (v’).

4.3 Analysis of BI

我们首先证明了VC（算法1）的正确性。为了简洁起见，我们只提供证明草图。
VC的正确性。给定q和G，VC可以基于BI找到从q到G的所有匹配项。
证明： (1)在算法1报告的M的情况下，BI保证M满足∀u∈V (q)、L(u)=L（M[u）)，算法1中的第14行保证M满足∀e（u，u0）∈E (q)、∃e（M[u]、M[u 0 ]）∈E (G)和M不包含任何重复的数据顶点。因此，VC报告的M是从q到g的匹配。(2)根据命题4.1和4.3，BI上的枚举等于g，因此，tVC的搜索空间包含从q到g的所有匹配。(3)BI中没有重复的候选和边。M不包含任何重复的数据顶点。因此，VC将不会输出任何重复的匹配从而证明了VC的正确性。
空间复杂性。BI包含两个组成部分：候选集和大集。由于在C中没有重复的候选候选集，而在BI中也没有重复的边，因此候选集C的大小为O(|V (G)|×|V(q)|)和大图的最坏情况大小是O（|E (G)|×（|V (q)|−1））（在BI中有|V (q)|−1大图）。因此，BI的空间复杂度为O（|E (G)|×|V (q)|）。
时间复杂性。函数生成指数次序对查询图的大小取时间多项式，由于查询图比数据图很小，所以可以省略。我们实现采用CFL[3]中提出的一种基于计数器的技术进行算法2的正向阶段，其时间复杂度为O（|E(G)|×|E(q)|）。算法2中的第14-20行最多取O(Pv∈u。c(v)×(u)时间。司同样，第21-23行也最多取O(∈v∈u。c(v)×(u)时间。因此，后退阶段（第12-23行）花费O(Pu∈V(q)Pv∈u。Cd(v)×d(u))=O（|E(G)|×|E(q)|）时间。因此，时间是复杂的算法2的ty是O（|E (G)|×|E (q)|）。算法4中的第5-8行需要O（|E (G)|）时间。因此，算法4的时间复杂度为O（|E (G)|×|V (q)|）。那么，构造BI的时间复杂度为O(|E(G)|× |E(q)|).
修剪功率比较。根据PSIC的定义，我们可以推导出以下引理。
引理4.2。给定q和G，C为完备性。如果（u，v）满足PSIC，其中u∈V (q)和v∈u.C，然后（u，v）满足∀u’∈N (u)，N (v) T u’.C = ∅.
然而，给定v∈u.C，（u，v）可能违反PSIC，即使它满足∀u’∈N (u)，N (v) T u’.C = ∅.
例子4.6。以图7c中的v2∈u2.C为例： v2满足N（v2）∩u’.C =∅和N（v2）∩u3.C =∅，而它违反了PSIC，因为N（v2）∩u0.C=N（v2）∩u3.C = {v0}。
因此，BI中PSIC的剪枝能力强于CFL的CPI中使用的观察结果。通过乒乓滤波策略，BI可以进一步减少候选集的大小。然而，作为BI和CPI用不同启发式规则生成的顺序提取候选数，我们不能从理论上证明BI得到的候选数小于CPI的候选数。相反，我们实验比较了BI与CPI的剪枝能力，实验结果表明，BI的剪枝能力强于CPI（见第6.4.1节）。

5 MATCHING ORDER GENERATION

在本节中，我们将介绍生成匹配顺序和枢轴字典的方法。

5.1 State Space Tree based Cost Model

我们首先定义了部分子图的同构性。
定义17 部分子图同构：给定q、G和π，q0是在π[1： i]上构造的q的顶点诱导子图，其中1 6 i 6 |V (q)|。一个部分子图同构（psi），记为f’，是从q’到g的子图同构。具体来说，当i = 0时，我们命名psi为初始psi，记为fr和fr = {}。
国家太空树探索。算法1的枚举阶段是基于递归回溯技术的，该技术在概念上动态地构造了一个状态空间树H。它从初始psi，并总是通过按照以下步骤的匹配顺序将查询顶点映射到数据顶点来扩展最近生成的psi。换句话说，它通过深度fi来探索Hrst搜索订单。H的初始状态为fr，内部状态为枚举过程中产生的部分子图同构。H的边对应于查询顶点之间的映射在BI中的候选人的匹配顺序。为了区分H中的边和图中的边，我们将H中的边称为一个动作。H的叶子是来自fr，wh的搜索路径的终止点ich可以分为两类：成功时，算法1中第11行的if条件为真，失败时，算法中第14行的if条件为假。所有成功的假期s是子图匹配的解。除了失败离开之外，从H的状态到psi存在一对一的关系。所以，我们把H中的非失效状态称为psi状态并表示为S。
例子5.1。图5d中的搜索树可以看作是VC在图1中的图上生成的状态空间树H。以节点s2为例。它对应于psi {（u0、v0）、（u1、v1）}、和s2下的动作将u3映射到BIu1 u3（v1）= {v6、v7、v8}中的每个候选对象。VC通过DFS顺序探索H，最终找到7个匹配项。
成本模型。给定q和G，VC探索H来找到所有的匹配项。因此，VC的成本，记为Tiso，可以通过H中的动作总数来估计，假设每个动作的成本是相似的。T他的H的最大深度，记为n，等于|π|。我们将fr的深度，即初始的psi，视为0。Ti表示在深度i下的psi状态下的作用数。然后，Tiso可以计算如下。

Ni表示深度i处的psi状态数，b i j为深度i处的第j个psi状态的搜索宽度，深度i处的psi状态的平均搜索宽度为bi。然后，T0 = N1 since深度1处的psi状态由算法1的第6-7行生成，其中没有候选状态被修剪，以及Ti = P j=Ni j=1 b i j = Ni×bi，其中1 <= i <= n−1。给定深度i的动作，其中1 <= i <= n−1，如果它能通过算法1的第14行的if-条件，则在深度i+1处生成一个新的psi状态。我们称这样的行动是一种有效的行动。Ni+1等于有效的活动体的数量在深度i。我们将有效因子αi定义为有效动作占深度i处动作总数的比例。因此，Ni+1 = Ti×αi和Ti可以计算如下。

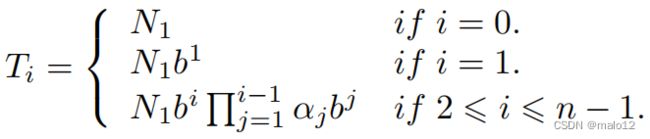
根据公式1和公式2，枚举的总成本可以计算如下。

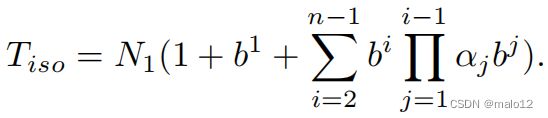
5.2 The Vertex-based Ordering

Tiso估计。为了最小化Tiso，我们首先通过检查枚举中影响参数的因素来给出Tiso中参数的估计。
给定q、G、π、P和BI，设S i j是深度i处的第j个psi状态。u是π中的（i+1）个顶点，其枢轴为u0。在S i j中，u’已经被映射到v’。在算法1中，过程枚举tr通过将u映射到v∈BIu’u（v’）来扩展S i j。S i j的搜索宽度b i j等于|BIu’u（v’）|。因此，bi可以被估计为|E（BIu0 u）| |u0。C-|，记为e-b-i。在算法1中，函数验证通过检查边b的存在来终止无效的搜索路径起着关键作用在一个候选v和BNq π (u)的映射数据顶点之间。如果你有更多的落后邻居，v有更高的概率。因此，αi估计为1 |BNq π(u)| 2，记为e αi。N1 is等于π[1]的候选者的数量。通过用我们的估计替换方程3中的参数，我们得到了总成本的估计Teiso，并优化了Teiso而不是Tiso。e αi由实际匹配顺序π决定。我们称π中每个顶点的对应e αi称为赋值。由于分配的数量等于查询顶点的排列数(|V (q)|!),动态地计算最优值太贵了。因此，我们提出了一种贪婪的方法来最小化Tiso。
贪婪的方法。一般的想法是选择αi值最小的查询顶点作为π中的下一个顶点，在早期对无效的搜索路径进行修剪，并最小化f psi状态在下一个深度。由于匹配的顺序是一个顶点一个顶点生成的，我们称之为策略基于顶点的排序。算法5概述了匹配顺序的生成。

第2行首先从q生成一个有向加权图qw，如下：对于每条边e（u，u0）∈E (q)，我们在qw中生成两条边e（u，u0）和e（u 0，u），w（u，u0）=m|。C|和w（u 0，u）=|u m 0 .C|，其中m是u中数据顶点之间的边数。C和u0。在数据图中的C。因此，如果我们选择u作为u0的枢轴点，w（u，u0）是e b i的值。
VC包含核心结构中的顶点，而VNC存储其他顶点（第3行）。我们将枢轴字典P初始化为空，并使用w∗[u]来存储minu0∈BNqπ(u)w（u0，u）(行4).基于定理4.2，我们在生成匹配顺序时，对核心结构中的查询顶点进行优先排序。此外，我们更喜欢从核心结构的致密部分开始枚举，并且起始顶点有少量的候选对象。因此，我们选择一个|u最小的顶点。C|.从核心结构中获得的核心值作为起始顶点（第6行）。如果VC是空的，我们就复制一个用VNC。无论何时修改w∗[u]的值，我们更新u的轴，以保持w（P[u]，u）（即估计的搜索宽度e b i）在w（u 0，u）中值最小，其中u0∈BNqπ(u)（第10行）。
我们处理VC中的顶点，并选择具有最小×eαi×eαi值的顶点（行12-15）。第16-19行处理不在核心结构中的顶点。对于每一个u∈UN∩VNC，|BNqπ(u)|=1，u.核=1和u.核度=0，我们使用(u)代替|BNq π (u)|。
时间复杂性。生成加权图的时间复杂度为O（|E (G)|×|E (q)|），其技术与算法4相同，算法5的其余部分的时间复杂度为O（|E (q)|）。所以，the算法5的时间复杂度为O（|E (G)|×|E (q)|）。
绑扎处理。当在第13行的最小函数中有联系时，我们更倾向于前导枚举，而不是q的密集部分。因此，分母|BNq π (u)|被以下属性替换为pri多数顺序为：(1)u核心；(2)u核心度和(3) d (u)。如果仍然有联系，那么顶点选择具有较低id的对象。具体来说，当|BNq π (u)| = 1为每个u∈UN∩VC时，我们使用绑定处理来选择顶点，因为算法1中的验证函数总是返回true|BNq π (u)| = 1.当在第5行和第17行处有连接时，将选择具有较低id的顶点。
例子5.2。图8a显示了从图5中的运行示例生成的qw。以e（u0，u1）∈E (q)为例。我们将它转换为e（quw）中的e（u0，u1）和e（u1，u0）和w（u0，u1）= 2和w（u1，u）0) = 1，因为在u0.C和u1.C之间有两条边，其中|u0.C| = 1和|u1.C| = 2。图8b说明了选择一个顶点的过程。一条边的起始顶点是结束顶点的支点x，权值是端顶点的w∗值。在图8b的顶部子图中，由于w∗[u3] |BNq π（u3）| 2 = 0.875小于w∗[u2] |BNπ q（u2）| 2 = 3，u3，和枢轴u3是u1。在此之后，w∗[u2]被设置为1，因为w（u3，u2）小于之前的w∗[u2]。
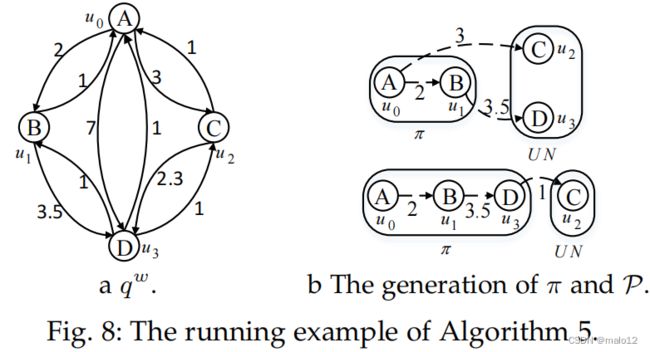命题5.1。将算法5生成的匹配顺序π连接起来，将核心结构中的查询顶点定位在π中的其他顶点之前。轴中的所有顶点对字典P构成了查询图q的生成树。

6 EXPERIMENTS

在本节中，我们进行了广泛的实验来评估VC在真实世界和合成数据集上的性能。

6.1 Experimental Setup

研究中的算法。我们在实验中评估了以下算法，它们有不同的指标和排序策略。
VC：我们的算法。它具有二部图索引BI和基于顶点的排序策略。
CFL [3]：最先进的算法。它具有树结构指数CPI和基于路径的排序策略。
GQL [11]： GraphQL算法。它具有邻域签名滤波器和左深连接排序策略。
QSI [23]： QuickSI算法。它没有任何指标，并采用了罕见的边优先排序策略。
此外，我们还将VC和CFL与其他两种采用基于路径的排序策略的SPath [28]和TurboIso [9]算法进行了比较。我们所有的实验中都没有涉及斯帕斯和turbo伊索，因为它们使用与CFL相同的排序策略，而且CFL优于它们。我们不考虑Boost技术[20]，它通过压缩数据图来加速子图匹配，因为根据[3]的实验，压缩有开销，CFL的性能优于CFL-Boost。
实验环境。我们从作者那里获得了CFL的源代码，并实现了其他源代码不可用的算法。所有涉及的算法都是用C-++和com实现的堆有g++ 4.9.3和-O3标志。我们在一台64位的Linux机器上进行了所有的实验，它配备了一个Intel Xeon E5-2660 v2处理器和32GB RAM。
数据图。我们评估了在以下真实和合成数据集上的性能。
真实数据集。我们选择了6个真实的数据集，它们在以前的工作中被广泛使用了[3]，[20]，[25]。酵母、人类、HPRD和WordNet最初包含标签。另外两个数据集没有唇形ls，我们随机地给每个人分配不同的标签。表2列出了详细的信息。
表2：真实数据集的属性，其中d为平均度，LF为标签频率，LF。SD是LF的标准推导。

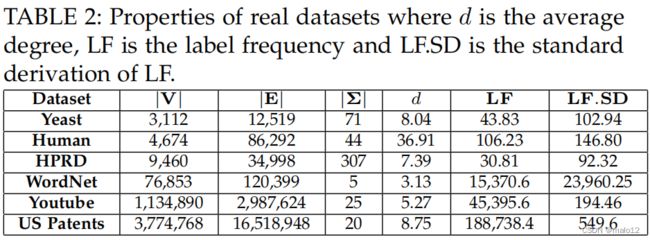
合成数据集。我们使用RMAT模型[4]生成合成数据集，并随机为顶点分配标签。为了检验算法在各种数据图上的可伸缩性，我们改变了|分别为V (G)|、d (G)和|Σ|。默认配置为|V (G)| = 100K（K = 103）、d (G) = 16和|Σ| = 30。
Vary |V (G)|：我们生成4个数据图，顶点数分别为100K、150K、200K和250K。
变量d (G)：我们生成4个数据图，其度度分别为8、16、24和32。
Vary |Σ|：我们生成了4个数据图，不同标签的数量分别为20、30、40和50。
查询集。根据之前的研究[3]，[20]，[25]，我们通过从一个数据图中随机选择子图来生成查询图，以确保至少存在一个匹配。对于每个数据图，我们生成8个查询集作为默认查询来评估竞争算法的性能，并生成4个具有大型查询图的查询集来检查它们的可伸缩性。每个查询集包含具有相同顶点数量的s 200个查询图。每个查询图都是连接起来的。具体来说，6个查询集包含非稀疏查询图（即平均度> 3），而其他6个查询sets包含稀疏查询图（即平均度< 3）。每个数据图的查询集如表3所示，其中qiN表示一组i-顶点非稀疏查询图和qiS表示一组i-顶点稀疏查询图。WordNet和Human的查询图较小，因为WordNet的76,853个顶点中有63,098个（即> 80%）同样的标签和人类都是非常密集的。因此，这两个图上的子图匹配比其他四个图更难。

指标。以前的算法的评估指标，它只检查查询集的平均执行时间和设置处理整个查询集的时间限制，可以隐藏的详细信息由于“掉队者”[13]，每个查询的执行时间。因此，在[13]之后，我们将分别检查查询集中的查询图。处理查询图的时间限制为10分钟(即6×105 ms).如果算法不能在时间内完成，我们将经过的时间记录为10分钟以便进行比较。详细的指标如下。
执行时间：在查询集中处理查询图的平均时间，它不包括从磁盘中加载数据的时间。它由索引时间和枚举时间组成。
相对性能：算法a对查询的相对性能是ta mina0∈a0，其中ta是a在查询上的执行时间，A是涉及的算法集。我们报告查询集的平均相对性能。该度量的最小值为1，表明该算法在查询集中的每个查询图上具有很强的竞争力。
执行时间类别：根据[13]中的设置，我们将在2秒内完成的查询分类为简单的类别，并在2秒到10分钟之间完成已完成的术语指的是在10分钟内完成的所有查询（简单和中位数）。由于时间限制而终止的查询称为硬查询。
为了比较不同的索引，我们使用以下指标。
索引时间：在索引阶段处理查询图所花费的平均时间。
索引大小：索引中用于处理查询图的候选对象的平均数量，用于评估索引的过滤能力。
#Embeddings.我们将要报告的嵌入数据的数量从103个到109不等。由于子图匹配的目标是找到所有的嵌入，所以我们将默认的嵌入数设置为109，以覆盖尽可能多的搜索空间随时间而变化。

6.2 Comparison with Existing Algorithms

评估执行时间。在图9中，所有算法通常会在更大的查询上花更多的时间。QSI、GQL和CFL的性能在不同的数据图上有所不同。CFL优于GQL和QSI在酵母、Youtube、美国专利和WordNet上，但在HPRD和Human的非稀疏查询图上表现比GQL差（在之前的研究中CFL没有与GQL进行比较）。VC始终被超越在所有数据图上，对现有算法改进了一个数量级（图9b、9c和9f），证明了VC的效率和鲁棒性。性能在HPRD上，GQL、CFL和VC之间的内存差距很小，因为大量不同的标签使得HPRD成为一个容易的查询数据集。在图9c和图9f中，QSI、GQL和CFL的曲线出现了变化对查询大小的增加。这是因为大量的查询不能在时间限制内完成（参见图11），它们的执行时间被替换为10分钟。因此，VC与现有算法之间的实际性能差距如图9所示，因为VC的硬查询数量比其他三种算法要少得多。

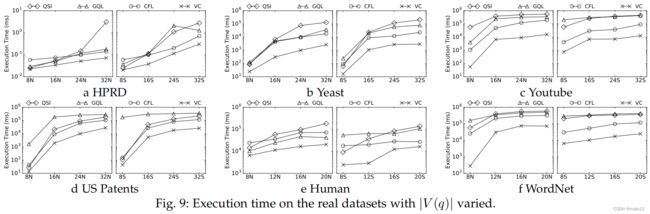
由于算法的性能在稀疏查询图和非稀疏查询图上有相似的趋势，因此我们只报告非稀疏查询图上的相对性能和执行时间类别的结果。
对相对性能的评价。如图10所示，VC在所有数据集上的相对性能都非常接近于1，并且在某些c上比其他数据集高出两个数量级（图10c和10f)。相比之下，其他三种算法的相对性能都低于1，因为它们处理了大量的假阳性候选算法，产生的结果较少有效匹配顺序比VC要好。

对执行时间类别的评估。所有算法都在两秒钟内完成在HPRD上的查询，所以我们省略了在HPRD上的结果。图11显示了其他五个数据集上的执行时间类别。中位数和硬查询的部分通常随着查询大小的增加而增加。VC更容易查询和比其他查询更少的硬查询，特别是当查询大小较大时。这一结果也反映了VC的效率和鲁棒性。

与斯帕斯和TurboIso的比较。在本实验中，我们比较了VC和CFL与SPath和TurboIso在HPRD和酵母上的作用。如图12所示，CFL优于TurboIso，TurboIso的运行速度快于SPath，这与之前的实验结果一致，[3]，[9]。此外，VC在四种算法中表现最好。

为了简洁起见，我们在以下实验中只报告人类和WordNet的q16N执行时间以及其他数据集的q24N的结果，除非我们声明我们使用不同的查询。

6.3 Scalability Evaluation

对合成数据集的评估。图13a显示了d (G)变化时的执行时间。随着d (G)的增加，所有的算法都需要更长的时间，因为d (G)的增长会导致时间的增加搜索广度的范围。VC的性能始终优于其他算法，当d (G) = 32时，VC和其他算法之间的性能差距缩小，因为现有的算法未能在一个大的n上完成当d (G) = 32时的查询数。在图13b中，所涉及的算法的执行时间随着|Σ|的增加而减少。当|Σ|值很小时，CFL、GQL和QSI存在严重的性能问题那么，搜索的广度就很大了。图13c为|V (G)|变化时的实验结果。与d (G)和|Σ|相比，|V (G)|对执行时间没有显著影响。

使用#嵌入数据进行的评估各不相同。如图14所示，当报告了更多的嵌入时，所有算法的执行时间都会增加，并且VC的性能始终优于其他算法。

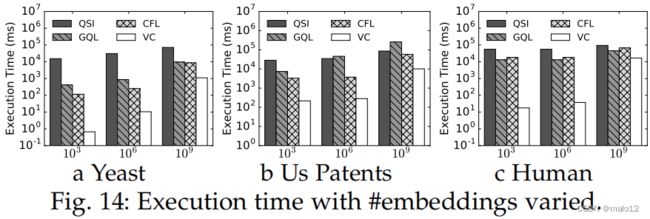
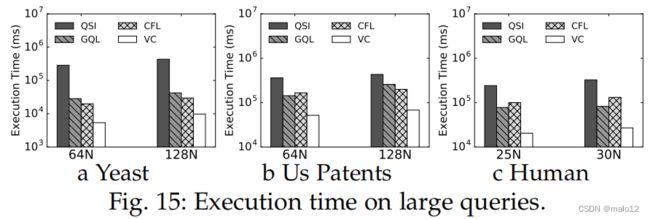
对大型查询的评估。图15显示了在包含大型查询图的查询集上的执行时间。VC比其他三种算法运行得要快得多，这表明VC的规模在大型查询上优于其他算法。

6.4 Effectiveness of BI and the Vertex-based Ordering Strategy

我们在VC中提出了两种技术： BI索引和基于顶点的排序策略。在本节中，我们将分别用真实的数据集来评估这些技术。

6.4.1 Effectiveness of BI

为了评估BI的有效性，我们比较了四种索引策略的索引大小、索引时间和索引内存成本。由于所有这些策略的空间复杂性都是O(|E (G)|×|V (q)|)，索引的内存成本在实际应用中非常小，并且它们在6个数据集上的每个消耗都小于10MB。因此，我们省略了关于索引内存成本的实验结果。
CPI：CFL[3]中的树状结构索引。它是由自上向下的生成和自下而上的细化构建的。
BI-Naive：由正向生成构建的BI指数。
BI-ESIC：基于精确的星形同构约束和乒乓滤波策略，通过正向生成和后向滤波构造的BI指数。
BI-PSIC：基于伪星同构约束和乒乓滤波策略的前向生成和向后滤波构造的BI指数。
对索引大小的评估。如图16a所示，BI-Naive比其他的对象生成了更多的候选对象，因为它没有任何过滤进程。BI-PSIC和BIESIC均获得较少的念珠菌菌这表明它们比CPI具有更强的过滤能力。BI-PSIC的候选者的数量几乎与BI-ESIC完全相同。因为人类是密集的和最垂直的在WordNet中有一个相同的标签，BI-PSIC和BI-ESIC分别比BI-Naive和CPI减少了约15%和21%的候选标签。
评价BI对VC的影响。我们分别将BI-Naive、BI-ESIC和BI-PSIC与VC集成，以评估不同的索引策略对VC性能的影响。图16c sh显示了在执行时间上的实验结果。比较图16b和图16c中的结果，我们发现索引时间主导了HPRD上的执行时间，而枚举时间，which是花费在枚举过程上的时间，在其他数据集上占优势。由于BI-ESIC的索引时间效率较差，BI-PSIC在HPRD上的性能高出3.2倍。在其他数据集上，BI-ESIC和BI-PSIC花费的执行时间几乎相同，并且都优于BI-Naive。虽然BI-PSIC和BI-ESIC与BI-Naive相比具有显著地减少了候选者的数量，但性能的改善并不那么显著（大约为1.26X-2.19X）。这种差异是因为VC中基于顶点的排序策略是由于同时考虑查询顶点之间的连通性，也考虑候选的数量，因此对假阳性候选的数量具有鲁棒性。
综上所述，BI-PSIC的滤波能力与BI-ESIC一样强，其构建指标的时间效率要快得多。因此，当索引时间占主导地位时，BI-PSIC的性能优于BI-ESIC执行时间，当枚举时间占优势时，也实现了类似的性能改进。
评价BI对现有算法的影响。为了进一步评价BI（BI与PSIC）的优点并显示其普遍性，我们将CFL、QSI和GQL与BI进行了集成分别分别为BI-CFL、BI-QSI和BI-GQL。如图16d所示，所有集成算法的性能都比原始版本得到了提高，因为(1) BI降低了假阳性候选序列的数量，为匹配顺序生成提供更准确的信息；(2) BI降低了搜索广度。此外，据我们所知，BI是第一个指标这可以与不同类型的排序策略集成，而之前的树状结构索引只支持基于路径的排序策略。

6.4.2 Effectiveness of the vertex-based ordering strategy

为了研究我们提出的基于顶点的排序策略的效果，我们将QSI、GQL和CFL中的排序策略与BI相结合。图16e显示了在不同排序策略下的实验结果ies.由于索引时间在HPRD上的执行时间，这些算法在HPRD上具有类似的性能。在其他数据集上，BI-QSI、BI-GQL和BI-CFL的性能各不相同在所有数据集上没有单一的赢家，包括基于路径的排序策略，这在以往的研究中被认为是一种有效的技术。相比之下，VC始终表现出色结果证明了我们提出的基于顶点的排序策略的有效性和鲁棒性

6.5 Integration with Existing Acceleration Techniques

一些研究人员[13]并没有设计新的子图匹配算法，而是试图利用现有的观测算法来加速子图匹配签名一个子图匹配算法这在所有数据集上的所有查询中都优于其他查询。他们提出了一个名为PSI的框架，它同时并行执行各种算法(每个算法实例在s中执行错误的)，并在一个算法实例完成时返回结果。为了评估VC对PSI的影响，我们比较了以下算法：PSI（包含QSI、GQL和CFL，3个线程），VC (1个3个线程d)和VC-PSI（包含BI-QSI、BI-GQL、BI-CFL和VC，4个线程）。如图16f所示，VC通过1.21-9.47X优于PSI，VC-PSI比VC能加速1.05-1.27X，这说明VC的signif显著提高了PSI的性能。此外，我们还研究了被VC-PSI加速的VC偏离者的数量。具体来说，如果VC-PSI运行，我们将查询视为VC的偏离者r在这个查询比VC快5倍。如表4所示，VC有少量的掉队者（总共有200个查询）。然而，由于VC在大多数情况下优于其他公司，PSI的好处是有限的VC。此外，PSI比VC消耗更多的计算资源。
除了并行化之外，PSI [13]还设计了查询重写技术，进一步加速了子图的匹配，它保持了查询图的结构，但重新分配了顶点的id遵循一些启发式规则，如度的降序。当在生成匹配顺序和集成顺序的过程中存在关联时，该技术会影响匹配顺序算法不处理这些关系。然而，由于VC具有设计良好的绑定处理策略，查询重写对我们基于顶点的排序策略影响很小。我们省略了这个实验为了简洁而重写查询的侮辱。

7 CONCLUSION

本文提出了一种新的子图匹配算法VC。通过将索引阶段划分为候选提取、匹配顺序生成和索引构建，我们打破了这一限制在基于树的框架中，[3]，[9]。利用伪星同构约束和乒乓滤波策略，沿索引顺序构造了一个二部图的过滤能力比索引结构在以前的工作[3]。最重要的是，通过将枚举抽象到状态空间树的探索中，我们提出了基于顶点的排序策略来解决由现有的订购策略引起的严重的性能问题。在真实数据集和合成数据集上的详细实验表明，VC取得了显著的性能提高比起现有算法。