【论文阅读】A survey of continuous subgraph matching for dynamic graphs

Wang X, Zhang Q, Guo D, et al. A survey of continuous subgraph matching for dynamic graphs[J]. Knowledge and Information Systems, 2023, 65(3): 945-989.

Abstract

随着信息技术的快速发展，多源异构数据已成为一个开放性问题，由于图结构能够对实体之间的复杂关系进行编码，因此通常将数据建模为图。然而，在实际应用中，如网络安全分析、社交网络舆情分析等，图数据的结构和内容在不断演变。因此，实时持续监控和检测海量动态图上有趣模式的能力对于许多应用至关重要。最近，还涌现了一大批优秀的研究著作。然而，这些研究侧重于图的不同更新，并应用不同的子图匹配算法;因此，最好全面回顾这些工作并给出一个彻底的概述。本文从关键技术、代表性算法和性能评估等方面系统地研究了现有的连续子图匹配技术。此外，还总结和展望了连续子图匹配相对于动态图的典型应用和挑战，以及未来的发展趋势。

1 Introduction

近十年来，社交网络、通信网络、万维网、金融交易网络等信息网络无处不在，无处不在。除了不断增加的数据规模和数据类型外，最重要的方面之一是由于现实世界的频繁更新，图形的结构和内容不断演变。以社交网络为例，Facebook 上有超过 14 亿的日活跃用户，每分钟产生超过 500,000 个帖子/评论和 400 万个赞，导致 Facebook 社交网络上的更新泛滥 [ 2 ]。此外，Google+ 自 2011 年推出以来的两周内增加了 1000 万新用户 [ 32 ]。因此，持续监测和检测感兴趣模式的能力对于在这种频繁更新的图形中获得有意义和最新的发现至关重要。同时，来自各个领域的许多应用程序都需要这种监控功能。

• 社交网络。这些应用可能涉及：1）有针对性的广告、垃圾邮件或欺诈活动检测[14,38,74]和2）假新闻传播监测[66]。
• 蛋白质相互作用网络。在蛋白质相互作用网络中，通过将已知的蛋白质网络与动态蛋白质相互作用网络相匹配，可以从蛋白质相互作用网络中快速找到突变的蛋白质结构[19,77]。
• 交通网络。在交通网络中，我们可以通过将模式图与动态路网数据图进行匹配来监测实时交通事故[66]。
• 计算机网络。在动态计算机网络中，基于连续子图匹配技术，我们可以及时监控网络攻击事件或检测异常流[17]。
• 知识图谱。它可以处理随时间推移而演变的知识，以支持连续的问答[13]，并且RDF图的推理也基于这种模式监控[6]。
  给定动态数据图和查询图，连续子图匹配问题可以描述为持续识别和监控动态数据图中的查询图，并报告匹配结果的最新更新。这里的匹配是指相同的结构并满足特定的语义约束。现在，我们以网络攻击事件检测和信用卡欺诈检测为例，说明如何将事件抽象为模式图，以及连续子图匹配的重要性。
  
  图 1 a 演示了基于图形的网络攻击模式描述。受害者浏览受感染的网站，导致下载恶意软件脚本。然后，恶意软件脚本在受害者和僵尸网络命令和控制服务器之间建立通信。当受害者在僵尸网络命令和控制服务器上注册时，他会同时收到一条命令，导致信息泄露回僵尸网络命令和控制服务器。显然，如果我们能够检测到网络中的攻击模式（基于子图匹配），则可以避免潜在的恶意活动。最近，美国通信公司Verizon分析了过去十年中的100,000起安全事件，发现其中90%可以很容易地归类为十种主要的基于图形的攻击模式[7]。
  
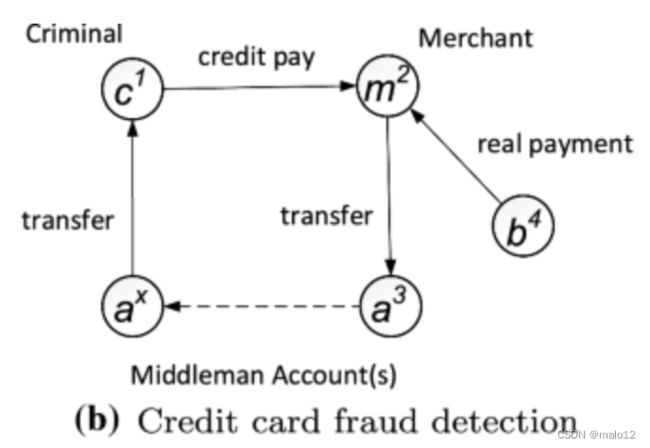
  图 1 b 显示了一个信用卡欺诈示例，其中包含一系列由模式图建模的交易。犯罪分子试图通过与商人和中间商进行虚假交易来非法套现。他们首先向商家建立信用付款;当商家从银行收到真正的付款时，他将钱转入中间人账户，中间人账户进一步将钱转回犯罪分子以完成兑现。显然，此模式也可以很容易地建模为查询图。通过在金融交易网络中检测这种模式查询，可以有效地避免欺诈。
  挑战和局限性。 由于连续子图匹配的重要性和实用性，如何在动态图上有效、高效地连续找到给定查询图的匹配结果，是大数据时代一个有意义的研究课题。通过观察其实际应用需求，我们确定了连续子图匹配可能面临的挑战列表：
• 频繁的数据更新。网络系统（如社交网络、数据中心网络或金融网络）中的图形数据一直在更新。因此，传统的静态图匹配技术需要重新构建索引，并在每次更新时重新匹配整个图数据，这是一种耗时且劳动密集型的方法。
• 大规模数据。由于不断更新，动态图数据量大于静态图数据量，增加了图子图匹配的难度。
• 对实时分析的需求增加。在许多实时分析应用中，每当图形更新时，都需要及时获得新的匹配结果;否则，匹配结果的应用价值将减少或丢失。例如，在网络安全中，需要实时监控可疑的数据传输模式，而分析匹配结果的延迟可能会导致网络瘫痪。
  进行这项调查的主要动机是双重的。首先，近年来提出了许多图算法来执行连续子图匹配任务;然而，现有的调查有些过时，没有讨论新的研究和建议。最新的调查[ 39 ] 发表于五年前，对动态图中的子图匹配只有简短的介绍。其次，调查[33]和[46]仅从某个方面对现有算法进行介绍和总结，并不全面。此外，现有的调查[47]只关注静态图中的子图匹配算法[36,63,85,87]。这些现有的调查没有对动态图数据上的连续子图匹配进行全面评价。特别是，我们的调查是第一个说明在动态图中的连续子图匹配领域在关键技术、代表性算法和性能评估方面所做的现有研究工作和进展的调查。同时，也有一些相关的调查，如模式挖掘[28]和社区搜索[27]。然而，前者侧重于动态图中的图挖掘，而后者侧重于大图的社区检索。虽然这两种技术都需要子图匹配算法，但这并不是它们技术优化的重点。
  在本次调查中，我们介绍了现有的连续子图匹配方法，这些方法致力于解决上述问题。首先，根据不同的实际应用需求，对连续子图匹配的研究进行系统分类;然后，我们讨论了基于动态图更新方法的两种不同类型的连续子图匹配方法。其中，针对图结构变化的连续子图匹配是研究最常的研究方法，增量匹配方法是解决该问题最先进的方法，它试图识别响应更新的动态图数据对先前匹配数据的变化，以满足日益增长的实时分析需求。
  本文的其余部分组织如下。第 2 节提供了连续子图匹配和分类的详细定义。第 3 节和第 4 节分别描述了基于结构和基于内容的更改的概念和匹配技术。第 5 节比较了不同匹配算法的性能。第6节介绍了连续子图匹配的当前应用。第 7 节列出了未来的主题，第 7 节。 8 提出了结论。

2 Definition and classification of continuous subgraph matching

在本节中，我们首先正式介绍连续子图匹配，然后从各种不同的方法论角度对连续子图匹配进行全面分类。

2.1 Preliminary definition

该图通常被定义为（V，E，L），其中V是一组顶点，E是一组介于两者之间的边，L是一个标签函数，它将每个顶点v，∈V与一组标签关联起来。任何边缘e∈图中的EG可以记为（vi，v j），其中vi，v j∈VG。在本文中，我们使用G =（VG、EG、LG）表示数据图，并使用P =（VP、EP、L P）表示模式图。目前，还没有两种数据图类型：超大图，如社交网络，或许多小图的组合，如艾滋病抗病毒数据集[5]，它包含许多显示原子的小图片化学物质的结构。由于目前的连续子图匹配问题主要涉及到超大型图，因此本文主要研究了超大型图的连续子图匹配问题。
动态图，也称为流图，是随时间演变的图。动态图更新分为两类，即（1）图结构更新，图中的顶点和边随时间推移入或删除，导致图结构发生变化;（2）图内容更新，其中图中数据对象的内容或属性被更新，导致内容发生变化。
动态图的定义将在下一节中给出。由于目前的研究主要集中在数据图的结构更新上，因此在图结构更新中给出了动态图的定义。

2.1.1 Graph structure update

定义1（图更新流）一个图更新流g由一系列更新操作（g1，g2，···）构造，其中g1是一个三重op，vi，vj，使op ={I，D}是一种操作的类型，I和D分别表示一条边的边插入和边删除（vi，v j）。
一个动态图抽象了一个初始图G=（VG、EG、LG）和一个更新流g。将g应用于G后，它转换为G.请注意，插入操作会在顶点和c之间创建新的边还可以添加新的顶点。对于删除操作也是如此。
定义2（子图同构）给定两个图G1=（V1、E1、L1）和G2=（V2、E2、L2），G1在G2（或从G1到G2）中的嵌入是一个双射函数f： (1) ∀v∈V1，L1(v) = L2（f (v)）；一个d (2) ∀(v1, v2) ∈ E1, ( f (v1), f (v2)) ∈ E2。
例3在图2中，虚线框显示了子图M =[（v1、u3）、（v2、u6）、（v3、u5）、（v4、u8）]，该子图通过更新操作将初始数据图G更为G1后与模式图P匹配ion g = {I, u5, u8}.

最近，图函数依赖关系[25]、键[21]和关联规则[24]都是基于子图同构匹配[62]定义的。然而，这是一个NP完全问题，因为所有可能的子图都会产生指数搜索空间[ 65 ] [ 35 ]。子图同构通常会对匹配过程施加更强的拓扑约束，以获得更一致的匹配结果。一些应用，如社交网络，对匹配精度要求不高，这极大地限制了匹配效率。鉴于其难处理性，已经研究了近似匹配以获得不精确的解，这允许顶点/边不匹配 [ 9 ， 70 ]。与近似匹配不同，模拟匹配不允许顶点/边不匹配。下面将更详细地介绍模拟匹配。
根据匹配近似的程度，可分为有界模拟[23]、图模拟[53]、对偶模拟[50]、强模拟[50]和严格模拟等e被统称为模拟匹配。有界仿真匹配通过从边到边映射移动到边到路径映射，放宽了同构匹配的严格结构约束.如果一个数据顶点u匹配查询顶点v，他们只需要满足L P (u)=LG (v)和LP（u）=LG（v），u是u的后代顶点和v是一个子顶点v与有界仿真相比，图仿真要求u是u的子顶点之一。这意味着顶点u与相应的节点 v保持相同的后继关系对偶模拟进一步要求u与v保持相同的前体关系。
在对偶仿真的基础上，强仿真要求包含匹配顶点的子图（子图可能包含不匹配的顶点）的半径不大于模式图的直径。严格的模拟匹配是模拟匹配中最严格的一种，它进一步要求完全由匹配的顶点组成的子图。
请注意，仿真匹配可以容忍匹配结果中的一些噪声和错误。因此，它在社交网络和Web网络分析等一些应用中发挥着重要作用。尽管仿真匹配结果与子图同构结果存在差异，但仿真匹配结果通常满足实际应用的需要。因此，它仍然被视为正确的匹配结果。以图仿真为例，其定义如下：
定义3（图模拟）给定一个模式图P =（VP，EP，L P）和G =（VG，EG，LG），图模拟是指P和G之间存在二元关系S⊆VP×VG，满足该关系:
(1) ∀(v, u)⊆S, LG (v)=L P (u)
(2)∀v∈VP，我们有： (a)∃u∈VG与（v，u）∈S，和(b)∀（v，v）∈EG，∃（u，u）∈EG与（v，u）∈S。

例4如图3所示，初始数据图G中的顶点u2与模式图p中的v2具有相同的标签此外，u2后继u4与v2后继v4具有相同的标签。那里因此，我们可以推断u2匹配v2。类似地，由于模式图P中的v3的后继者是空的，我们可以推断v3与u3匹配。因为在u4的后继者中没有顶点，它的标签是与v4的后继者相同，v3、u4和v4不匹配。因此，根据图模拟匹配的定义，对于t = 1，在初始数据图G后更新操作GC2={I、u4、u6}，u4和v4满足匹配条件。此外，子图M1 = [（v2、u2）、（v3、u3）、（v4、u4）]和M2 = [（v2、u2）、（v3、u6）、（v4、u4）]与生成的模式图相匹配。需要注意的是，虽然结构M2的结构与模式图P不同，但它仍然被认为是匹配的。

2.1.2 Graph content update

图内容更新意味着图形中顶点/边或特定对象评估的标签可以随时间变化。

示例5如图4所示，对于时间t = 1，我们改变了初始数据图G中的u3和u6的标签。虚线框显示了子图M = [（v1、u3）、（v2、u6）、（v3、u5）、（v4、u8）]，其中为在数据图被更新后，获取模式图。

2.2 Classification of continuous subgraph matching

在本小节中，我们根据五个方法论角度对连续子图匹配进行分类，并介绍每个类别的代表性算法。由于每个分类都不是独立的，因此每个分类的算法之间存在交叉点。

2.2.1 Dynamic feature of data graph

从数据图的动态特征来看，根据图的拓扑结构是否发生变化，将连续子图匹配分为结构变化和内容变化。目前，许多关于连续子图匹配的研究主要集中在数据图中顶点或边的动态添加和删除引起的结构变化。主要用于网络异常攻击检测和社交网络关系检测。Wang等[75]在2009年首次提出了结构变化的连续子图匹配。他们构建了一个节点邻居树（NNT）来过滤匹配的候选集，可以有效减少负匹配结果。随后，提出了一些具有代表性的算法，包括IncIsoMatch[23]、SJ-Tree[16]、图仿真（DDST[66]和IncBMatch [23]），进一步提高了子图匹配的执行效率。
图形的内容更改主要出现在数据中心。许多研究将数据中心的网络拓扑结构抽象为数据图进行数据分析，其中图中的每个顶点代表一个服务器，顶点之间的边代表服务器之间的链接。在这种情况下，图数据的拓扑结构不会频繁变化，但数据图中顶点的标签（即服务器的可用内存量）和边（即链路的有效带宽）会随时间频繁变化。为了有效处理这种情况，BoZhong等[88]提出了Gradin算法。提出了用于跟踪演化数据的N维网格索引，也可以直接应用于数据图中频繁更新的边缘标签。

2.2.2 Strength of consistency constraint

从一致性约束的强度来看，根据是采用双射函数还是二元关系，连续子图匹配可分为子图同构和模拟匹配。子图同构保证了匹配结果与模式图完全一致。主要用于蛋白质相互作用网络分析[39]、网络异常行为监测[17]等结构要求严格的数据分析应用。
而仿真匹配则通过二元关系得到结果，匹配结果为近似匹配。首先，根据数据顶点的标签生成每个查询顶点的匹配候选集，然后根据模式图中顶点的前体和后继点的不同近似匹配度，过滤掉不匹配的顶点。具有代表性的算法包括DDST[66]和IncBMatch[23]等。特别是，即使子图的结构与模式图不同，IncBMatch算法得到的结果也满足匹配条件。同时，IncBMatchcan的匹配过程在多项式时间内进行，效率更高。仿真匹配更加灵活，提高了匹配效率，识别出更有用的匹配结果。因此，它主要用于监测道路网络上的交通事故[66]，并检测人与各种群体之间的关系[23]（如毒品交易关系网络）。这个图数据分析应用程序更侧重于挖掘顶点之间的关系。

2.2.3 Type of matched results

从匹配结果的类型来看，由于所获得的匹配结果的准确性，连续子图匹配算法被归类为精确算法或近似算法。精确算法保证了匹配结果的完全准确，主要应用于网络异常检测、生物数据分析等多个领域，这些领域依赖于准确的匹配结果。用于匹配数据图和模式图的精确算法示例包括 IncIsoMatch [ 23 ]， SJ-Tree [ 16 ] 和 Gradin [ 88 ]。
但是，许多使用实时结果的应用程序要求快速返回所有匹配结果，这使得复杂的精确匹配算法变得不合适。巧合的是，这些应用程序也可以容忍一些顶点/边不匹配（即假阳性结果）。针对这些问题，该文提出近似子图匹配算法。它与模拟匹配不同，因为它通常基于概率统计等数学模型。通过参数调整，匹配结果的误差比可以保持在一定范围内。所有研究成果都提出了NNT[75]、复制机制[55]和SSD[30]，提出了一种近似图匹配算法，将图匹配问题转化为更容易解决的问题，以匹配精度换取匹配效率。
需要注意的是，精确算法和近似算法是决定匹配结果准确性的两种算法，而子图同构和仿真匹配是不同类型的图匹配模型。

2.2.4 Computational environment

从计算环境来看，连续子图匹配可以是集中式的，也可以是分布式的，根据是部署在分布式平台还是单机上。集中式连续子图匹配在单台计算机上运行，采用基于连接或基于探索的匹配方法，主要处理小规模图数据。基于连接的匹配方法对查询图进行分解，匹配每个查询片段，然后将获取的匹配结果连接起来。通常，此方法需要构建索引。基于探索的方法[69]从数据图中的一个顶点开始，根据查询图的结构探索整个数据图。与基于联接的匹配不同。此方法不需要生成索引。
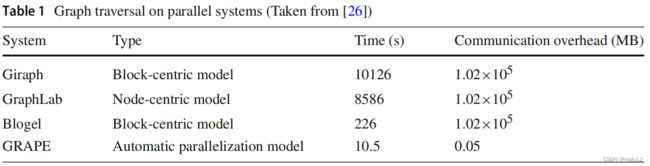
分布式连续子图匹配主要依靠分布式并行图处理框架来处理规模大、计算复杂度高的动态图数据。目前主流的分布式并行图计算系统有三种类型，分别是以顶点为中心的模型（包括Pregel [ 51 ]， Trinity [ 64 ]， Giraph [ 1 ]， 和 GraphLab [ 49 ]）、以块为中心的模型 （Blogel [ 78 ]， BLADYG [ 11 ]） 和自动并行化模型 （GRAPE [ 26 ]）。其中，以顶点为中心和以块为中心的模型需要根据模型的特点对算法进行修改，不熟悉的用户很难对并行模型进行重铸。相比之下，自动并行化模型不需要这样做;它只需要用户为具有少量内容的数据图提供三种顺序（增量）算法。现有算法的逻辑不需要修改。此外，3个分布式并行图计算系统均遵循BSP模型[72]，由于需要对匹配结果进行增量更新，分布式匹配通常采用基于探索的方法进行分布式匹配。
表 1 显示了不同类型分布式并行图计算系统在最短路径查询方面的性能。以美国路网为数据集，可以发现GRAPE系统的性能明显优于其他类型的系统。

2.2.5 Dependency relationship of queries

从查询的依赖关系来看，连续子图匹配也可以根据连续子图查询是表示为一个或多个更新的图流，分为单查询应答或多查询应答。现有算法主要贡献于单个查询答案，其中查询被设置为独立隔离和评估。目前，动态图的单查询应答技术已经相当成熟，如NNT [ 75 ]， SJ-tree [ 16 ] 和 SSD [ 30 ] 所示，其中算法使用一次查询方法：分别优化和回答每个查询。它们不允许批处理多个查询。然而，当多个查询到达时，顺序处理并不总是最有效的 [ 62 ]。
Zervakis等[83]首先提出了一个基于动态图的连续多查询过程引擎TRIC。为了充分利用来自多个查询的信息，它将它们分解为多个覆盖路径，并构造一个索引来组织路径。每当发生更新时，它都会利用查询集中的共享限制来持续评估查询。多查询的关键点是 （1） 快速检测每个更新的受影响查询，以及 （2） 避免成本高昂的联接，并探索适用于大型查询集的方法。
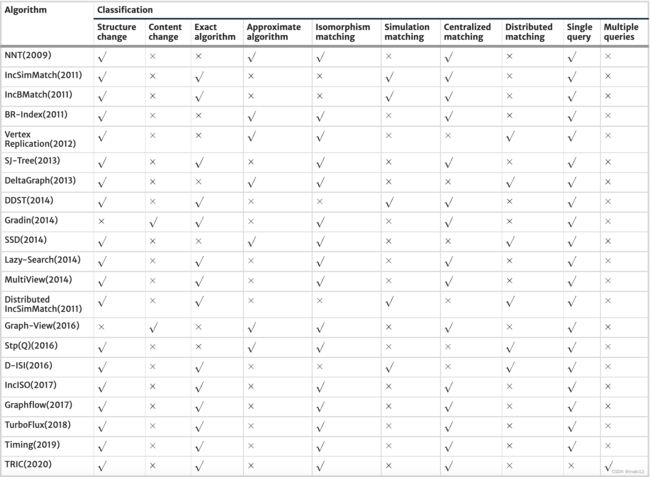
总之，所提出的每种算法和分类都是不同的，并解决了不同的图匹配问题。表2总结了具有代表性的连续子图匹配算法及其分类。以下各节将详细介绍基于基于结构和内容变化的连续子图匹配技术。在每一节中，将对主要问题进行分析和比较，并讨论每种匹配技术类型的代表性算法和研究现状。由于目前大多数研究都围绕着基于结构的变化的连续子图匹配问题，本文将主要关注基于结构的变化的图匹配技术的最新研究进展。

3 Continuous subgraph matching for structure-based change

基于结构的变化的连续子图匹配是目前使用最广泛的技术。从算法设计的角度来看，目前存在两种基于快照的匹配技术（Sect. 3.1）和增量匹配（Sect. 3.2 ）. 基于快照的匹配技术将每个时间戳的更新数据图视为静态图，以执行匹配算法。相比之下，增量匹配技术仅对数据图的更新部分进行分析和匹配，避免了重新匹配整体数据图的不必要计算。此外，增量匹配技术的更细粒度分类在章节3.2中进行了详细描述。 在图5中总结了结构变化连续子图匹配技术的分类和代表算法。

3.1 Snapshot-based matching technique

基于快照的动态图匹配技术被认为是一个大规模的静态图匹配问题，因为每个时刻的每个更新数据图都是一个静态图。然后，在这些连续的静态图流上执行匹配算法。它通常适用于有许多附加边缘的情况。在这种情况下，可以同时完成所有边的添加，并在更新的数据图快照上执行匹配算法。因此，基于快照的匹配技术包括更新操作和匹配操作两部分。下面对这两种操作进行讨论。

3.1.1 Data graph update

Wang等人首先在[75]中讨论了连续子图匹配问题。本研究将不断更新的图数据视为图流，并采用基于快照的模式匹配提出了NNT算法，取得了良好的性能。NNT算法为数据图G和模式图P中的每个顶点u构造了一个节点-邻居树（NNT）记为NNT (u)。对于数据图G，给定深度值L，NNT (u)（u∈G）存储数据图G中的所有路径，将u视为根顶点，长度不超过L. As图5a、T1、T2、T3、T4为数据图g，深度值L = 2对应顶点1、2、3、4。表示顶点标签的大写字母为t1和t2的元素是相同的。图6b显示了NNT找每个NNT中与数据图中的顶点和边相匹配的节点和边，其中∗表示反向索引中省略的部分NNT的反向索引。

动态图结构变更的更新操作包括删除边操作和添加边操作。以下讨论显示了每个操作如何使用基于 NNT 的倒排索引来更新索引。
删除边操作：假设数据图中的一条边在某个时间被删除，则必须通过倒排索引同时删除所有 NNT 中对应的边和子边。对于图中的数据图G。 5 ，如果删除边 （1， 3），则从倒排索引中删除边 （a， c）、子边 （c， e） 和 （c， f） 以及与这些边T1&T2 关联的顶点。
添加边操作：如果在某个时间将一条边添加到数据图中。首先，根据倒置的索引，找到每个NNT中与所加边的节点对应的顶点。然后，t他从数据图中新生成的路径添加到NNT中，从对应节点的顶点开始。对于图6中的数据图G，如果添加了边（1,4），则在T1中，添加了路径（a→g→h）从顶点a加起来，其中顶点g和h的属性分别为C和B。在T2中，路径（b→g）从顶点b开始添加，其中g的属性为→。加边操作为在添加nnt中的所有路径时完成。最后，需要通过添加新添加的顶点和边来更新反向索引。类似地，也需要在节点4上执行相同的操作通过来更新索引结构。
NNT算法将模式图与数据图在每时刻的快照进行匹配，并不能反映图随时间的演变过程。Yang等[81]首先提出了一种用于大规模动态图的索引结构BR-Index，该结构将数据图划分为一系列重叠的索引区域。每个区域都包含几个独立的核心区域。提取每个索引区域的最大特征（小子图），然后建立特征格进行维护和查找。同时，它还维护了一个基于哈希原理的顶点查找表。该表用于存储每个索引区域中的数据顶点，以及该顶点在索引区域中的哪个核心区域。因此，当数据图更新时，可以使用查找表快速定位更新的部件。
此外，Song等[66]提出了一种基于时间窗的子图匹配算法DDST，这是第一个对图流施加时序约束的工作，其中窗口包含所有满足时间约束的快照。此外，每个边上都有一个时间常数，用于记录边的生成时间。根据此时间戳，可以确定合法数据子图是否在给定的时间窗口内。只有当窗口中的合法数据子图满足匹配条件时，才会成为匹配结果。与NNT算法相比，时间窗方法的优点是它能够随时间推移演化图，并且更符合实际应用。
此外，Khurana等[42]提出了一种树状索引结构DeltaGraph。它是一个有根有向图，其中每个叶节点存储一个按时间顺序排列的快照，内部节点存储一个由组合较低级别的图组成的图。在这里，根节点表示源节点，叶节点表示目标节点，每个边都包含来自源节点和目标节点的信息。当数据图执行添加或删除边操作时，此索引结构会将当时数据图的快照添加到叶节点。与每条边一起存储的信息称为边增量。并且构建图的源节点（即根节点）与图的目标节点（如叶节点）对应就足够了，这样就可以通过遍历路径来创建从根到快照的特定快照。当数据图执行添加或删除边操作时，此索引结构只需要将该时刻数据图的快照添加到叶节点中即可。

3.1.2 Subgraph matching

在匹配过程中使用子图同构方法时，时间复杂度非常高。例如，对于使用子图同构方法进行匹配的NNT算法，时间c复杂性可以描述为O（n1∗n2（|T1| 1.5/log|T1|）|T2|）[81]，其中n1表示模式图中的顶点数，n2表示每个tim的数据图中的顶点数e、t1和t2表示模式图和数据图对应的最大nnt个数。这表明，子图同构方法严重限制了其执行效率NNT算法；因此，这不满足连续子图匹配的实时要求，应尽量避免。
NNT算法采用一种近似算法，通过比较NNT中两个顶点的路径来进行子图匹配。如果NNT中的所有路径都是由每个模式图的顶点c构造的在由相应的数据图顶点构造的NNT中查找匹配，表示模式图与数据子图相匹配。该子图匹配方法的时间复杂度为O(n1n2rl )，其中r表示数据图节点的最大度，l表示所选的深度值。因为每个匹配操作都需要匹配所有可能的顶点，所以开销仍然很高。因此，该算法还提出了一种将NNT转换为数值向量的编码方法，并计算所有NNT中不同路径的数量，以进一步减少计算开销。
如图6a所示，T1、T2、T3、T4中有8条不同的路径，因此，每个顶点的NNT可以用一个8维向量表示，其中第i维记录了……的数量在NNT中的第i条路径。因此，模式图和子图可以转换为一个多维的数值向量。如果模式图中的每个维度的值都小于或等于l为子图中维数的值，表示子图满足匹配条件。基于上述优化的匹配时间复杂度为O（Ln1n2），其中L表示n数值向量中非零项的数量。
在子图匹配过程中，BR-Index算法首先提取模式图的特征（子图）集。然后，根据这个提取的集，它在数据图中查找包含其中一些特征的索引区域。接下来，它会在相应的索引区域中查找这些特征的候选集。最后，将候选集组合起来，得到匹配结果。
相比之下，DDST算法使用仿真匹配方法来完成子图匹配。由于仿真匹配比同构匹配更灵活，因此可以识别出更有用的结果。然而，在子图同构中，传统的图仿真将边到边映射扩展到边到路径映射，并施加了更灵活的拓扑约束，导致结果不精确。为了解决这个问题，DDST算法在图仿真中增加了两个约束条件Dual simulation和Locality [ 50 ]，并构造了模式图的特征。签名包括边和顶点的标签，以及所有顶点的入度和出度信息。如果数据子图的签名与模式图一致，则按顺序使用二进制模拟。同时，它在模式图中显示边的时间顺序。如果数据子图中每条边的时间属性满足模式图中的时间顺序，则满足匹配条件。进一步，DeltaGraph 使用分布式并行图处理框架完成子图匹配;它将快照存储在内存中。给定一个模式图，它可以使用边缘上的信息直接从根开始找到匹配的快照。
综上所述，子图同构方法计算效率低，耗时长。因此，近似匹配算法和仿真匹配算法更适合设计基于快照的匹配方法。近似算法利用少量假阳性结果减少匹配时间，仿真匹配利用二元关系的验证来代替子图同构。模拟匹配主要应用于更注重顶点之间挖掘关系的应用。最后，根据应用需求确定最合适的子图匹配算法。

3.2 Incremental matching technique

对动态图形使用基于快照的匹配方法将导致许多冗余计算，即使只有少量更新操作也是如此。对此，范文飞等[ 23 ]首先将增量处理技术应用于连续子图匹配，提出了IncSimMatch算法和IncBMatch算法，该算法仅对数据图的更新部分进行分析和匹配。此外，他们将这两种算法分别与批处理（快照）算法 Matchs和 Matchbs进行了比较。实验结果表明，当初始数据图中边的添加或删除操作次数不超过边总数的一定百分比时，增量匹配技术的执行效率更高。
增量匹配是指给定一个数据图G、一个模式图P、一个初始模式图匹配结果P (G)和一组针对数据图G的更新操作，以及一个新添加的匹配结果设置O将在数据图更新后计算。这是P（G⊕G）= P (G)⊕O，其中⊕表示用于将更改后的内容添加到原始数据中的操作符。
在匹配过程中，增量匹配技术既可以使用直接计算方法，也可以构建一个辅助数据结构来利用中间结果。的优势和下面将详细讨论这两种方法的缺点。

3.2.1 Direct computation

当添加或删除一条边时，它可能只影响子图的一小部分。因此，范文飞等[23]提出了一种基于直接计算的增量算法IncIsoMat图模拟方法。它识别并提取了一个可能受到Oi影响的子图G。它在G上执行一种子图匹配方法，通过确定得到对原始匹配的变化设置原始匹配和新匹配之间的设置差异。Wenfei Fan等人[22]进一步提出了另一种关于增量子图同构的直接计算方法IncISOm.当数据图被更新时，只对更新边周围的模式图直径范围内的数据图节点进行重新匹配，以避免对整个数据图的双重计算。IncISO的代价可以表示为|P|和|GdP (G)|的函数，而不是整个图大小的|G|，其中Gd (v)表示v在d跳内的d−邻居子图。
虽然上述算法通过匹配受影响的小规模子图中的子图来减少冗余计算，但它们也产生了新的性能问题。这些方法都是基于重复使用的方法搜索在提取受影响的子图G时可能会产生显著的开销。Gd (v))，在G上执行子图匹配。Gd (v))，并计算每个Oi的新匹配。此外，由于两个顶点之间的平均距离非常小，提取的子图G(Gd (v))可以包括G中的大部分节点和边，从而得到一个无用的优化。
在处理连续子图匹配的图数据库方面，许多现有的图数据库，如Neo4j [3]和OrientDB [4]，只支持评估子图的一次性子图查询对数据图的每个快照进行说唱。然而，由于实时性的需求，需要许多应用程序来处理连续的子图查询。为了解决这个问题，坎坎南格等人[40]提出提供了一个活动的图形数据库，图形流，它支持为每个更新进行增量子图评估。在内部，系统的查询处理器是基于通用连接[58]的，它本质上是一个最坏情况下的最优连接算法[57,73]。此外，Ammar等人[10]进一步将最坏情况下的最优连接扩展到分布式系统。
给定一个模式图P =（V §，E §），泛型连接首先确定一个查询节点的=u1，u2，…，u|E§|，，然后使用多向交叉操作实现一个多向连接查询节点依次依次，根据顺序s。查询节点的每个顺序也可以被视为一个查询计划。在子图匹配问题中，可以实现多路交点ng由一个或多个查询节点匹配的邻接列表上的交集操作。在实现的过程中，查询节点的顺序，s，确保，对于任何小于|E (Q)|的k，诱导d子图由s=u1组成，u2，…，uk被连接。这里，诱导子图用Pk表示。通用连接的整个过程包含两个基本操作：
扫描：对于查询节点上的前两个节点，通过扫描图的邻接列表，直接得到顺序s=u1，u2，…，u|E§|。
扩展/相交：当获得Pk−1匹配时，可以通过扩展/相交运算符计算Pk的匹配。对于Pk−1的任何匹配，与uk相邻的查询节点的每个匹配都开始了沿着其邻接表获得所有可能的匹配为uk；然后，这些匹配被交叉，以获得uk的最终匹配。
虽然图流可以处理基于通用连接的连续子图查询，而不计算集差，但它仍然需要对每个Oi甚至i从头开始计算连接操作fOi不会导致任何新的匹配。

3.2.2 Auxiliary data structure

虽然采用直接计算的增量匹配算法是在受Oi影响的小规模图上进行的，但仍然需要从头开始在小图上进行子图匹配f或每次更新，导致高昂的计算成本。为了解决这个问题，可以构建一个辅助数据结构来跟踪之前计算的（部分）结果。然后，对于e每次最近的更新，都可以很容易地获得更新的结果。
在构建辅助数据结构的过程中，中间结果可以存储在查询图或数据图中，称为查询中心表示或数据中心表示，分别。在构造辅助数据结构，找到所有查询顶点的候选集后，执行查询图的子图匹配操作。下面深入介绍了基于两种不同的辅助数据结构的子图匹配。
以查询为中心的表示方式以查询为中心的表示方式比较常用，它为每个查询顶点存储一组候选数据顶点，并且通过遍历可以获得部分匹配正在显示查询图形。在子图匹配过程中，连续子图匹配类似于静态子图匹配。根据模式图是否需要分解，它可以使用其中任何一种一种基于连接的匹配技术或一种基于探索的匹配技术。此外，基于图仿真的匹配技术在连续子图匹配中也得到了良好的实验结果。下面将深入介绍了这三种方法。
(1)基于连接的匹配技术
对于一个大型的模式图，每次更新数据图时，重新测试整个模式图可能是很耗时的。因此，而不是寻找与整个草原的任何边缘的匹配或查询图，最好将查询图分成更小的子图，然后搜索它们。如图7所示，模式图P被分解为一系列较小的模式子图图，表示为P1，…，Pk.然后，这些模式子图与单个子图跟踪匹配，并将匹配组合起来，以逐步生成的最终匹配结果轮胎图案图。

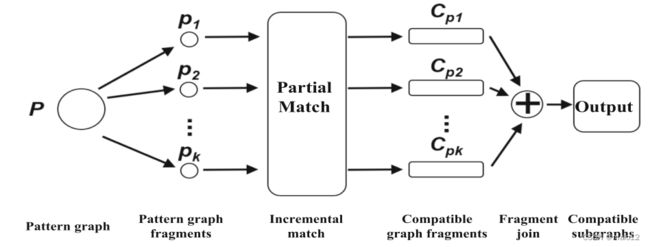
基于连接的方法在静态子图匹配中得到了广泛的应用。具有代表性的算法包括gIndex算法[80]和GraphGrep算法[31]。基于连接的方法使用数据图中的识别功能挖掘特征，例如路径 [ 31 ， 87 ]， 树 [ 63 ， 82 ] 和子图 [ 15 ， 37 ， 80 ]。基于这些特征，它可以在数据图上构建索引并分解模式图。然而，简单地将这种方法应用于连续子图匹配过程会产生一系列问题。例如，gIndex 算法 [ 80 ] 需要在每一时刻挖掘数据图子图的特征。因此，该方法不适用于具有实时分析要求的连续子图匹配处理。虽然 GraphGrep 算法 [ 31 ] 满足实时性要求，但仅使用路径可能会产生几个负面结果;因此，不强烈建议将其用于验证和过滤应用。值得注意的是，当将基于连接的方法应用于连续子图匹配分析时，数据图特征的高效提取是主要挑战。
在社交网络应用程序中构建的数据图通常是多关系图。边的属性表示实体之间的连通性和关系。因此，在该应用中，可以将数据图实体之间的关系（即边的类型）用作数据图特征来分解模式图。Choudhury等[16]提出了一种树状的辅助数据结构，称为子图连接树（SJ-Tree）。SJ-Tree 是一个二叉树，其根节点表示模式图，其子节点表示模式图的子图。然后，对每个节点的子图进行进一步分解，得到它们的子节点。叶节点表示最终的分解结果。

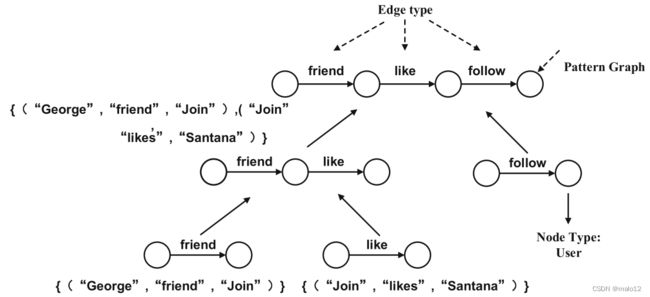
如图所示。 如图8所示，SJ-Tree中的每个节点都存储了其同级节点和父节点的信息，并维护了一个哈希表来存储该节点的匹配结果。当数据图更新时，对SJ-Tree上的所有叶子节点进行迭代搜索，得到包含新添加边的匹配结果;此匹配结果存储在SJ-Tree中相应节点的哈希表中。同时，在可能的情况下，将叶节点的匹配结果与其同级节点的匹配结果集成，以形成更大的匹配结果。较大的匹配结果存储在父节点的哈希表中。此外，还定义了一个连接顺序，其中各个匹配的子图将被组合在一起。当生成与整个模式图匹配的结果时，连接操作完成。图 8 显示了使用 SJ-Tree 分解社交查询的示例。SJ-Tree {（“George”， “friend”， “Join”）} 和 {（“Join”， “like”， “Santana”）} 的叶节点候选集可以连接和集成，形成更大的匹配结果 {（“George”， “friend”， “Join”）， （“Join”， “like”，“Santana”）}。
尽管SJ-Tree可以在相对于其高度的指数时间内执行图形查询，但它仍然有局限性。在图中。 8、由于在子图匹配过程中，数据图中经常出现“朋友”关系，因此跟踪所有匹配“朋友”的边无疑需要相当长的时间。因此，可以推迟匹配形态图中的“朋友”边，首先匹配数据图中出现频率相对较低的分解结果。基于这一思想，Choudhury等[18]提出了一种懒惰搜索算法。给定初始数据图 G，图 G 中 k 边子图 g 的选择性是 g 出现次数与 G 中所有 k 边子图数量的比率，其中 g 称为选择性基元。为了限制子图同构的计算成本，并在数据图更新时保持选择性原语的有效性，通常选择单边或双边子图作为选择性原语。Lazy-search 算法采用离线方法计算数据图中包含的单侧或双边子图类型的选择性，并根据其选择性值对这些选择性基元进行升序排序。选择性值越低，识别能力越高。随后，根据这些选择性基元的顺序分解查询图。
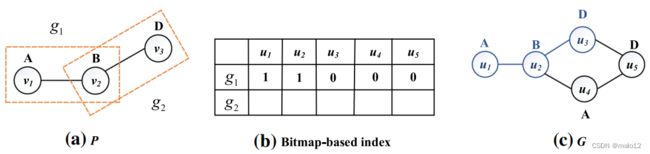
在匹配过程中，为了确保SJ-Tree中相邻叶节点的匹配结果在数据图上仍然相邻，它构造了一个位图索引，如图9b所示。钍e行表示数据图中的所有节点，列表示满足邻接关系的模式图的分解结果。图9a显示了两个相邻的d2c如果数据图的顶点在查询片段g1的匹配结果中，则对应的位为1，其他的位为0。例如，如g1匹配s为数据图中的边（u1、u2），对应于g1的u1和u2的位为1，其他位位置为0。当匹配g2时，只有满足g2 aro匹配条件的结果和需要在g1中找到位图向量为1的顶点。这个优点是它可以使用相邻的分解结果来确保匹配的结果在d上仍然相邻ata图形。因此，它可以避免不满足邻接关系的匹配结果，减少搜索空间，加快匹配过程。

基于分解和连接方法，Youhuan Li等[48]研究了具有时间顺序约束的连续子图匹配，即流中边的出现跟随t并提出了定时子图匹配算法。所有的匹配结果都应该同时满足结构约束和时间约束。具有双时序顺序约束的查询图Q的一个例子整数如图10所示，1≺2表示匹配1的边应该在匹配2的边匹配2之前到达。在图10中，查询被分解为一组只包含一个时间顺序约束的子图查询称为定时连接查询，并为每个子图查询Qi构造一个匹配存储树（MS-tree）来存储中间结果G（Qi）。然后，得到了子图的所有中间结果根据定时顺序约束进行连接，得到最终的匹配结果G (Q)={G（Q1）、G（Q2）、G（Q3）}。

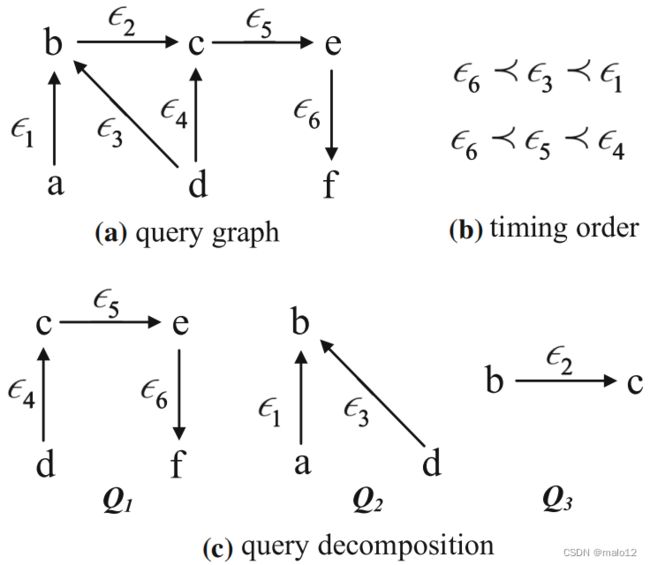
基于定时顺序约束，MS-Tree可以过滤掉大量可丢弃的部分匹配项，从而降低空间成本和维护开销，而不会产生任何额外的数据访问负担。与前面提到的具有时间约束的DDST算法不同，它基于子图同构而不是图模拟。更重要的是，它旨在执行有效的并发管理，在计算中使用细粒度锁定技术来提高系统吞吐量。这是第一项研究子图匹配与流图并发管理的工作。
基于连接的匹配技术在匹配过程中使用子图同构，可以获得准确的匹配结果，但代价是昂贵的。尽管查询分解方法可以控制子图的大小并限制子图同构的成本，但它仍然会产生许多无效的中间结果。如果为数据图构建索引以减少无效中间结果的数量，则还应考虑索引构建和维护的成本。同时，如何对频繁更新的动态图数据进行特征结构挖掘，进行查询分解，仍是一个亟待解决的问题。
（2）基于探索的匹配技术
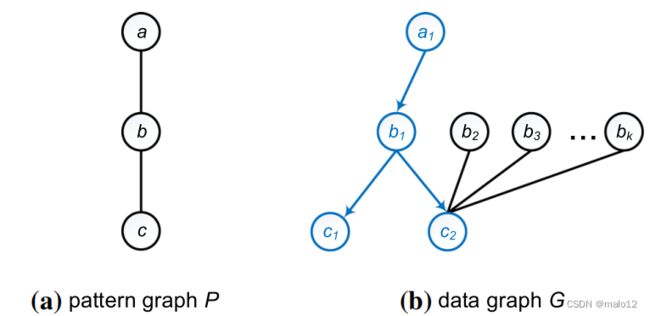
基于上述问题，Sun等人[69]提出了一种基于探索的匹配技术，其中得到的结果是近似的，而不是精确的。勘探过程的一个例子如图11所示。给定一个模式图P和一个数据图G，该技术从模式图中的顶点a开始，通过一个简单的索引th找到数据图G中匹配的顶点a1在映射标签到节点id。接下来，从顶点a1到顶点b1，探索数据图，满足部分查询（a，b）的要求。然后，从b1探索到c1和c2，me满足部分查询的要求（b、c）。这样，它就可以从数据图中获得模式图的匹配结果，而不需要生成和连接较大的中间结果或就像基于连接的匹配技术一样，为数据图构建和维护索引。当然，如果该方法从一个标记为b或c的节点开始，它仍然可能会得到一些无用的插入结果。但一般来说，除非在最坏的情况下，否则它不会产生那么多的结果。基于探索的匹配技术的有意义的优点是避免了连接操作。

相较于基于连接的连续子图匹配，基于爆炸离子的连续子图匹配更适合分布式并行图处理框架。主流的分布式并行图处理框架，如谷歌的Pregel[51]系统，都使用以节点为中心的计算模型框架。对于此框架，每个顶点维护一个输入队列和一个输出队列。此外，每个计算任务都由一系列超级步骤组成。在每个超步中，顶点接收到来自输入队列的输入信息后，会根据用户自定义的脚本程序对信息进行处理，最后将处理结果输出到输出队列中。由于存储和处理单元都是顶点，这种计算模型与基于连接的连续子图匹配一起会产生多个中间结果，从而增加了顶点的处理、存储和数据传输成本。综上所述，基于连接的连续子图匹配技术不适用于分布式并行图处理框架。相比之下，基于探索的方法更合适，因为它不需要索引构建，也不会产生和处理大量的中间结果。此外，它自然满足了增量计算的潜在需求。
PathMatch 算法是一种基于探索的匹配技术，用于分布式并行图处理框架。它在模式图中查找可以访问图中每个顶点的哈密顿路径。使用此路径传输信息以完成探索（匹配）。但是，如果我们将基于探索的匹配技术应用于分布式并行图处理框架，它仍然面临以下问题：
首先，基于探索的方法得到的匹配结果是近似的，而不是精确的;
在求解一些连续子图匹配问题时，使用一个朴素的图探索比连接操作更昂贵；
并非所有查询都可以通过仅依靠探索来回答，例如，在尝试检查下一个探索的顶点是否是第一个匹配的顶点时。
为了解决上述问题，Sun等[69]提出了一种新的探索方法STwigMatch，该方法最大限度地发挥了基于连接的方法和基于探索的方法的优点，同时避免了它们的缺点。具体而言，该方法在宏观层面上采用基于连接的图匹配框架和基于探索的匹配方法，避免在连接过程中出现无用的候选者，并找到匹配结果。换言之，它基于模式图中传输的信息，而不是数据图中提取的特征子图，将模式图分解成一系列小树枝，然后将每个分解结果存储在分布式并行图处理框架的一个顶点上。后来，它通过基于探索的方法匹配这些小树枝。此算法的优点是可以在匹配计算成本和匹配结果准确性之间进行权衡。
此外，Gao等[30]在分布式框架Giraph中提出了一种基于探索的算法SSD。图 12 是 SSD 算法的计算过程图示。首先，在形态图中将具有最大度的顶点标记为下沉顶点（即图中的顶点C）。 12 a）。它被称为接收器，因为所有满足的边缘都传递给它，并且它不需要发送消息。选择汇顶点后，通过BFS（广度优先搜索）策略确定边的方向。基于这个概念，模式图可以转换为具有单个汇顶点的有向无环图（DAG），如图所示12b。而将下沉顶点作为切割顶点，DAG可以进一步分解为三个子DAG。在每个子 DAG 中，都有一些源顶点（例如，子 DAG 0 中的顶点 a 和 e），它们没有任何传入边，可以初始化消息传输。
图 12 c 显示了子图匹配的过程。在子 DAG 0 中，信息传递到其所有邻居（顶点 1 和顶点 2）以从顶点 0 转换。然后，转换后的信息继续传递到它们的下游邻居，并最终到达顶点 3。因此，它可以从源顶点获取信息传输规则。然后，将信息传输规则映射到数据图中，从数据图中属性与源顶点相同的顶点开始，根据规则检查后续顶点是否与查询顶点匹配。例如，在图中。 如图12 C所示，源顶点0匹配数据图顶点A，匹配过程通过一系列超步骤完成。在超级步骤 1 中，顶点 a 将信息传递给其邻居;在超级步骤 2 中，顶点 B 和 C 在接收到信息后将信息传递给顶点 D。如果顶点 d 接收到来自同一顶点的两条信息，这与子 DAG 0 的信息传输规则相同，则可以证明存在匹配的子图。

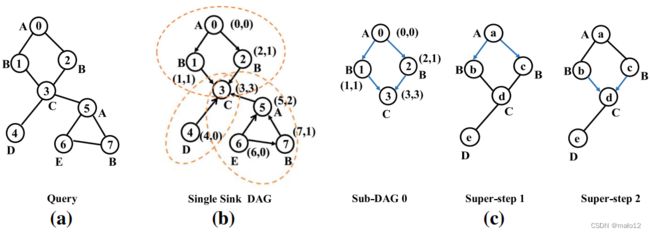
但是，SSD算法仍然存在问题。在超级步骤 2 中，如果在顶点 b 和 c 将信息传递给顶点 d 时删除了边 （a， b），则顶点 d 在接收到信息后将返回过期的、不准确的匹配结果。在分布式系统中，由于每个分布式并行图计算框架都包含许多超级步骤，因此结果不一致的问题很严重。为了解决这个问题，Gao等[29]提出了Stp（Q）算法。
基于探索的匹配方法更适合处理大规模图;但是，不一致的匹配可能会产生不准确的匹配结果。因此，这种类型的方法适用于对结果精度要求不严格的应用，例如社交网络分析。确定如何有效地结合基于探索和基于连接的匹配方法，以平衡效率和子图匹配精度是当前研究的热点问题。
3）基于仿真的匹配技术
请注意，基于探索的匹配技术会产生不准确的匹配结果，而基于连接的匹配技术则成本更高。两种方法均采用NP-hard子图同构匹配方法，限制了性能的提升。因此，基于仿真的匹配技术在连续子图匹配领域备受关注。该方法根据每个查询顶点的标签为每个查询顶点生成一个匹配的候选集，然后根据查询顶点的前体和后继点的不同近似度过滤掉不匹配的顶点（参见 Sect. 2.1 有关模拟匹配的详细信息）。
范文飞等[ 23 ] 提出了一种采用辅助数据结构 match（v） 和 candt（v） 的增量图模拟匹配 （IncSimMatch） 算法，以保持中间结果并加速匹配计算。这里，v 表示模式图中的顶点，match（v） 表示数据图中与 v 匹配的顶点，candt（v） 表示数据图中与 v 具有相同标签但不满足其他匹配条件的顶点。
使用这些辅助数据结构，可以过滤掉不必要的更新操作：
对于删除边操作，只有当被删除的边，如（ui，u j）满足ui∈匹配（·）和uj∈匹配（·）时，才会导致匹配结果的减少。
对于添加边缘操作，在当添加的边，如（u∈，u j）满足u∈匹配（·）和u∈匹配（·）或u∈匹配（·）和u∈匹配（·）时，将产生一个新的匹配结果集。
此外，范文飞等人扩展了初始仿真匹配的定义，提出了有界仿真的概念，该概念重新定义了具有边缘权重的模式图。模式图中的每条边都保持一个常数 k。如果数据图中有一个顶点与 k 跳内模式图中相应顶点的后继顶点匹配，则存在匹配。进一步将有界仿真匹配技术应用于连续子图匹配，并提出了增量算法IncBMatch。IncBMatch 算法与辅助数据结构 match（v） 和 candt（v） 提到的 IncSimMatch 算法类似，解决了高度复杂的同构匹配问题，取得了良好的效果。有界仿真匹配的优点是可以在多项式时间内完成匹配过程，有效提高了子图匹配的效率。
文献[41]是最早将IncSimMatch算法应用于以顶点为中心的分布式并行图处理框架，实现动态图仿真匹配的分布式并行计算的工作。在匹配过程中，更新后的图形存储在框架的顶点中，执行脚本允许顶点过滤掉不会产生新匹配结果的边。然后，通过框架的顶点，根据图仿真匹配中的边约束关系对边进行评估。主进程将接收来自所有顶点的处理信息，然后评估这些子图在图仿真匹配中是否满足边缘约束关系，以获得最终的匹配结果。
然而，仿真匹配方法基于二元关系，可能会产生与模式图结构不一致的结果;因此，它主要适用于对图结构匹配要求不是很严格的应用，例如社交网络分析。此外，模拟匹配可用于修剪候选集。Wickramaarachchi等[76]提出了一种基于动态图的分布式剪枝算法D-IDS，该算法使用对偶仿真匹配方法对数据图进行剪枝。双重仿真要求当前节点的所有子节点和父节点都符合二进制关系。当数据图更新时，使用二进制模拟对数据图进行剪枝，可以将较大的数据图修剪为相对较小的数据图。同时，数据图可以连续维护。在匹配过程中，只需要对小图进行增量匹配。
仿真匹配匹配效率高;它适用于分布式和集中式环境，并具有一些独特的优势。这种优势在连续子图匹配的处理中更为明显。基于图仿真匹配的双向仿真匹配可以更好地权衡仿真匹配结果的有效性和时效性，同时获得更符合模式图结构的匹配结果，从而有效弥补了基于连接的匹配技术和基于探索的匹配技术的缺点。
虽然构建一个辅助数据结构来存储中间结果可以减少重新计算的开销并获得更好的性能，但以查询为中心的表示仍然有几个l模仿当一个数据图顶点v有多个候选查询顶点时，v需要复制的次数是匹配查询顶点的次数。此外，还存储了许多部分的结果和然后按照一定的顺序相互连接确实会导致大量的冗余。具体来说，SJ-tree最糟糕的存储复杂度是O（|V (q)|∗|E (G)| |E (q)|），其中|E (G)|表示图G中的边的数量，V (q)表示图q中的顶点的数量。最后，当顶点v发生任何更新时，它必须在以查询为中心的对象中找到包含v的所有部分匹配项表示因此，它需要设计和维护一个重复键的额外索引，以在以查询为中心的表示中找到相应的部分匹配。
数据中心表示现有方法的所有上述问题都促使[43]去研究新的概念表示，称为数据中心图（DCG）。它存储了相应的查询顶点ID，作为数据图中每个数据顶点的传入边标签。因此，在DCG中，每个数据顶点最多出现一次，并且每个数据边最多存储在|V (q)|边上。因此，它是我们的最情况的存储复杂度为O（|V(q)|∗|E(g)|）。
在动态图中，执行模型允许进行快速的增量维护。DCG中的每条边都有三种状态之一： NULL、隐式或显式。一个显式边（v，u，v）表示该query顶点u是v的候选顶点，u的数据路径和子树与v.对应的数据路径和子树相匹配在隐式边（v，u，v）中，只有u的数据路径与co匹配v，的r响应数据路径和子树不匹配。当插入/删除一个新的/过期的边时，TurboFlux使用一个边转换模型来改变每个对应的边的状态，和f在内部，它可以基于显式边报告正/负匹配。此外，与其他辅助数据结构相比，因为DCG本身是一个图，每当DCG更新时，它就可以di直接访问相应的顶点；不需要像以查询为中心的表示那样的额外的重复键索引。
图13显示了DCG的一个运行示例。图13显示了查询图q的数据图经过转换后得到的DCG。当将（v0、v1）插入到g中时，(v0、u1、v1的状态)在DCG中将从NULL转换为隐式，因为插入的边匹配（u0，u1）和v0有一个输入的标签u0的显式边（图13）。然后，将（v1、u4、v4）的状态转换from NULL为隐式，因为v4是v1的子顶点，（v0，u1，v1）的状态是隐式的（图13e）。接下来，将边缘的状态（v1、u4、v4）转换为显式状态（图13f)。请注意：v1的子树与u1的子树相匹配。因此，（v0、u1、v1）的状态被转换为显式（图13g)。最后，sam的（vs∗，v0，v0）的状态也从隐式转换为显式e原因（图13h)。

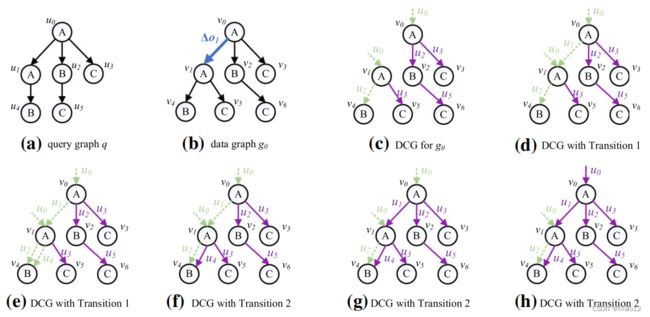
综上所述，TurboFlux通量简洁的辅助数据结构和高效的增量维护策略使其成为目前最先进的方法。它可以有效地识别更新操作这可能会导致与当前的部分解的正/负匹配。

3.2.3 Complexity analysis

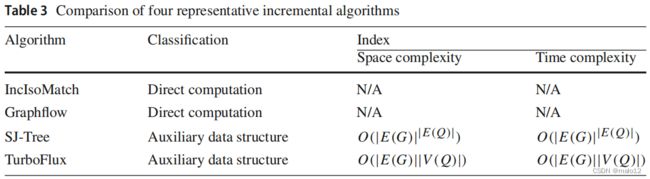
连续子图匹配算法的目的是在在线数据图流上找到给定模式的出现。数据图的动态特性要求匹配的结果需要to，我很快就会得到回应。因此，增量连续子图匹配算法得到了广泛的研究。在表3中，我们总结了索引的空间复杂度和时间补偿四种最新且具有代表性的连续子图匹配算法的每次更新，包括IncIsoMatch，树树、图形流和涡轮流量。积分匹配和图形流是直接计算增量算法，它们不生成任何辅助数据结构。而sj树和涡轮通量常利用一个辅助的数据结构来加速过滤速率。
从表3中可以看出，对于SJ-Tree，辅助数据结构（索引）的空间复杂度和时间复杂度是指数级的，而对于TurboFflux，它们则是线性的。这是因为SJ-Tree建立了一个树形索引，并使用了大量的连接操作。TurboFlux使用了一个以数据为中心的表示方式来存储候选集。显然，涡轮通量可以有效地减少搜索空间。

4 Continuous subgraph matching for content-based change

除了基于结构的连续子图匹配外，还研究了基于内容的连续子图匹配技术。例如，使用这种技术，可以在经常更新的数据中心网络中找到满足用户需求的服务器部署解决方案[60];广告商可以在频繁变化的社交网络中找到紧密联系的人群;HR可以基于约束模式图在动态社交网络中构建团队[44]。这些应用程序中节点或边的标签会随着时间而频繁变化。目前，关于基于内容的连续子图匹配技术的研究较少。以下是一些典型的研究。

4.1 Join-based matching approach

Bo Zong等[88]以数据中心网络中的资源分配为应用背景，提出了Gradin算法，用于解决用户自定义资源模式图与数据中心网络之间的连续子图匹配问题。它采用基于连接的匹配方法，因为数据中心网络具有相对稳定的拓扑结构，但节点/边缘标签频繁变化，这代表了空置的 CPU 周期和网络带宽。匹配过程将包括以下两个阶段。
离线索引构建：首先，通过现有的结构选择算法[80]确定频繁图结构集，然后通过子图挖掘技术[79]获得数据中包含频繁图结构的所有图片段。基于这些频繁的子图，在数据图上构建倒排索引。
在线查询处理：Gradin 使用基于连接的方法来搜索模式图的兼容子图。首先根据频繁的子图对模式图进行分解。然后，Gradin 将每个查询片段的候选者搜索到向量，并使用索引来有效地搜索它们。然后，它通过连接操作将查询子图的所有匹配片段组合在一起，形成模式图的兼容子图。
显然，频繁的更新是一个需要解决的巨大挑战。因此，Gradin算法进一步使用了一个基于网格的索引，分形滤波器，它可用于构建自由度的索引图中的元子图，避免冗余比较。如图14所示，让1表示从数据图中挖掘出的频繁子图。然后，对数据图中的所有子图都具有相同的特征作为s1的结构可以根据其节点标签转换为二维向量，并进一步映射到二维网格索引，即分形滤波器中的所有黑点。同时，与模式图中s1结构相同的子图也以用红方块表示的相同方式映射到网格索引。如果模式图的子图与数据图的子图相匹配图中，对应节点的标签必须满足部分阶。因此，二维网格可以根据红方块的位置分为三个区域。数据图的子图，对应于落在度中的黑点N个阴影区域r1将满足与图案图的子图的匹配要求。相反，数据图的子图，对应于落在棕色阴影中的黑点Ow面积R3不满足与模式图的子图的匹配要求。因此，只需要对黑色对应的子图进行匹配计算点在绿色和棕色阴影区域之间的区域（即R2），以得到匹配的结果。

在搜索处理中，Gradin算法需要将dns/λd[（λ+1）/2]d−平均匹配1次，其中λ为网格索引的密度，d为网格索引的维数，ns为离线索引构建过程中的模式图切片的数量。当数据图的节点/边标签经常更新时，分数滤波器的维护成本低于其他索引结构平均而言，每次图形更新只需要2次（1次−1/λd）操作。
Gradin算法也可以直接扩展到数据图中的边缘标签频繁更新的情况。除了使用在数据图中挖掘的频繁子图来解密之外提出模式图，目前学术界常用的高级子图结构也可以用于模式图的分解。

4.2 Exploration-based matching approach

然而，基于连接的方法不能直接扩展到大型动态图[ 69 ]，它适用于具有静态或不经常更新标签的查询。由于动态图中的活动属性会导致连接索引的大量更新。因此，Mondal等[56]设计了一种基于探索的查询评估系统，称为CASQD，以基于子图匹配来持续检测有意义和最新的见解，而不是内容变化图。
基于探索的方法的原理是选择一组潜在的枢轴节点，然后探索它们的邻居以获得匹配。这种方法的关键是如何有效地选择枢轴节点，并充分利用有关相邻节点的附加信息。因此，CASQD 使用基于监控、探索和触发器的方法来选择枢轴节点并减少搜索空间：
监控：在监控阶段，CASQD 通过一组模型汇总活动节点和/或其活动邻居。监控策略有两种捕获活动信息的方法：（1）直接评估节点的活动谓词并实时跟踪其活动邻居的数量;（2）通过历史信息计算活动节点的概率“估计”。
探索：在探索阶段，如果一个节点 v 周围有基于其模型和邻居知识的匹配，则称为枢轴节点。探索阶段在枢轴节点周围搜索匹配项，并找到可能的结果。此外，它还使用探索阶段收集的信息进一步更新了枢轴节点的邻域知识。
触发：触发阶段用于让活动节点的邻居了解任何重大更改，并据此更新其知识。
与 Gradin 相比，该设计的优势在于不需要在数据图上频繁进行子图挖掘，高级子图结构可以集成到任何支持子图模式匹配的查询语言中。此外，CASQD将简单的树状结构模式扩展到更复杂的结构，例如星星，clique，二部clique，并设计了不同的探索算法来寻找不同的原始模式。

5 Performance comparison of matching algorithms

在本节中，我们分别总结和分析了代表性算法在不同分类下的性能。我们主要侧重于分析基于结构变化的连续子图匹配方法的性能。
数据。 此评估中使用的多个真实数据集和合成数据集涵盖了广泛的设置，包括：
麻省理工学院数据集：取自麻省理工学院媒体实验室的移动通信信息，以2004年1月至2005年5月97名固定人员的移动通信信息子集为实验数据集;生成了 300 个图快照。每个快照都表示动态图在特定时刻的状态。
合成数据：它是使用图形生成工具生成的。
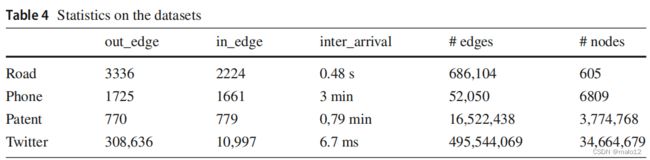
真实数据集的集合：包括路网交通数据、电话通信数据、专利引用数据、Twitter数据等。表 4 给出了这些数据的详细统计数据，包括数据集的最大进/出度、增加边的平均时间间隔以及节点和边的数量。
纽约时报数据集：包含 39,523 个节点和 68,682 条边。
livejournal：在线社区网站LiveJournai的友谊网络，拥有4,847,571个节点和68,993,773条边。
YouTube：有 14,829 个节点和 58,901 条边，其中每个节点代表一个视频对象，该对象记录了长度、类型和其他属性。
引文网络：有 17,292 个节点和 61,351 条边，其中每个节点代表一个论文对象，记录了论文的标题、作者和出版年份。
LSBench：包含包含 20,988,361 个三元组的初始图形和一个包含 2,332,065 个三元组插入的图形更新流。

查询图。本节中使用的常见查询图是通过从数据图中随机提取子图，对每个大小和查询类型抽取100个查询。有两种类型的查询：树形和图形（具有循环）。而查询图还可以根据密度进一步分为两种类型：稀疏（davg≤3）和致密（davg > 3）。稀疏查询和密集查询都是图查询。对于每个type，查询图由|V (Q)|生成，从4到12以2为增量变化。
指标。 对于结构变化的连续子图匹配算法，最常见的评估指标是查询处理时间，即给定图更新流的在线处理经过的时间，以及中间结果的大小，它显示了算法的剪枝优化能力。此外，在基于探索的方法比较中，还评估了传输的消息和精度。而对于内容变化的连续子图匹配算法，过滤时间和查询处理时间是主要的评价指标。

5.1 Structure-based change

根据第2.2 节的分类方法。 基于结构的连续子图匹配技术分为基于快照技术的匹配和基于增量技术的匹配两种。本节将介绍这两类算法的性能评估。

5.1.1 Snapshot-based technique

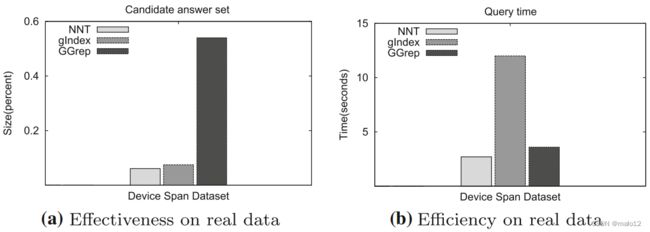
所有算法的性能都可以从有效性和效率的角度来评估。Wang等[75]使用真实和合成数据集将所提出的NNT算法与gIndex [80]和GraphGrep [31]进行了比较。真实数据来自麻省理工学院媒体实验室的移动通信信息[8]，以2004年1月至2005年5月97名固定人员的移动通信信息子集为实验数据集;生成了 300 个图快照。每个快照都表示动态图在特定时刻的状态。使用图生成工具[45]生成合成数据。
实验结果表明，在有效性方面（如图1所示）。 15 a），GraphGrep算法使用超过50%的匹配结果作为候选集，导致剪枝能力差，有效性低。NNT算法和gIndex算法在有效性上没有显著差异，因为NNT算法产生的候选集低于6%，而gIndex算法的候选集在6%10%之间。在效率方面（如图所示）。 15 b），gIndex算法的查询时间明显高于其他两种算法。这可以归因于gIndex中频繁使用的子图挖掘方法。虽然匹配结果的有效性很高，但每个快照都需要频繁挖掘数据图的子图，非常耗时。NNT 和 GraphGrep 算法不需要挖掘子图特征，因此效率更高。
与静态图上使用的基于连接的匹配技术（gIndex算法）相比，基于快照的连续子图匹配技术可以从两个方面进行改进。第一种方法是设计有效的索引结构，可以高效地处理数据图的更新，并利用索引的剪枝能力来有效减小匹配候选集的大小。第二种方法是使用逼近算法，牺牲一些精度来换取更高的匹配效率。
在 [ 66 ] 中，介绍了几个真实的动态图数据集，包括路网交通数据、电话通信数据、专利引用数据和 Twitter 数据。同时，将所提DDST算法与NNT算法进行了比较。NNT算法不使用时间窗约束，而是使用基于同构匹配问题的近似算法。请注意，这会导致匹配结果出错。在比较中，DDST算法考虑了数据图更新边缘上的时间约束关系，并使用了基于仿真匹配问题的精确算法，从而获得了更准确的结果。由于算法的性能需要在相同的实验环境下进行对比，因此在比较过程中需要忽略时间约束和结果的准确性;仅从吞吐量的角度比较了算法的效率。
如图所示。 16、实验结果表明，对于道路和电话数据集，DDST算法的吞吐率显著高于NNT算法。同时，随着窗口范围的增加，NNT算法的吞吐率降低。这是由于NNT算法在索引维护上花费了大量的资源，对数据的增加更敏感，并且采用了更严格的同构匹配方法。相比之下，DDST使用图形模拟方法，在吞吐量（效率）方面表现出优越的性能。
综上所述，为了满足实时应用的需求，可以考虑以下两个角度来设计基于快照的匹配技术。首先，需要设计一个有效的指标结构。这将确保在更新数据图的过程中不会存在过多的索引维护成本。此外，还需要设计一种近似算法来提高效率。其次，使用仿真匹配，需要在图仿真的基础上增加限制，以更好地满足实际应用的需求。此外，需要设计一种基于仿真匹配二元关系的精确算法，以提高算法的匹配效率。使用同构匹配或仿真匹配基于特定的应用程序背景。

5.1.2 Incremental technique

随着连续子图匹配中增量技术的出现，越来越多的研究关注这一领域。增量技术更适合于实时更新的图数据，可分为直接计算和构建辅助数据结构两大类。此外，所应用的子图匹配算法可分为三种类型：基于连接的匹配、基于探索的匹配和基于图的模拟匹配。接下来，对这三类连续子图匹配算法的性能进行了分析和比较。最后，对不同代表性的增量算法进行了综合比较。
（1）基于连接的匹配技术
Choudhury等[ 16 ] 在2011年8月至10月期间使用真实的《纽约时报》数据集比较了SJ-Tree和IncIsoMatch算法。在图中。 17、实验结果表明，SJ-Tree比IncIsoMatch更快，并且随着数据图大小的增加，两种算法的性能差距也越来越大。这可以归因于这样一个事实，即增量匹配技术在匹配过程中围绕每个新到达的边进行搜索。对于 IncIsoMatch，当新边到达时，需要找到边缘端点周围 k 跳范围内的所有节点，其中 k 表示模式图的直径。当数据图密集时，k-hop 范围内的子图会积累大量边，使得搜索成本更高，查询速率更慢。对于使用查询分解的SJ-Tree，将一个大的匹配图转换为一系列较小的匹配图，使算法更加高效。

而[17]中提出的选择性惰性搜索方法可以根据具有识别能力的选定结构对候选集进行过滤，有效地减少了搜索空间。实验计算结果表明，子图同构操作在查询过程中占总查询时间的95%，从而减少了子图同构的数量。这可以有效地提高算法的性能，并导致搜索速度为VF2算法[20]的10∼100倍。
此外，Youhuan Li等人的[48]比较了定时算法、sj树和其他三种最先进的静态子图匹配算法的时间效率和空间效率在受影响区域的窗口上形成，包括QuickSI [63]、TurboISO [34]和BoostISO [61]。显然，定时算法比其他方法更快。这是因为TiminG算法使用增量策略，而不是为每个时间窗口重新计算每个快照。同时，首先根据时序序常数过滤出一些可丢弃的部分匹配使用MS-tree，而SJ-tree需要枚举所有部分匹配以找到过期的匹配。
以上实验结果表明，如果整个模式图与数据图匹配，特别是密集数据图，进行增量匹配会导致效率较低。特雷夫如果分解模式图是一种选择，但可能会产生许多无效的中间结果。同时，对于基于连接的匹配技术，使用子图同构验证方法d，无效的中间结果将导致匹配效率的进一步降低。因此，通过选择特征结构进行查询分解，无效的中间结果可以被过滤掉以加快匹配速率（图18)。

(2)基于勘探的匹配技术
Gao等[30]在分布式平台Giraph [1]上比较了SSD与STwigMatch和PathMatch算法。该研究使用了真实的数据集livejournal。STwigMatch 使用了基于 STwig 的分解框架和基于探索的匹配方法。PathMatch 方法仅使用基于探索的匹配方法。该实验使用查询时间和传输的消息总数作为评估指标。如图所示。 19、SSD算法和STwigMatch的性能总体上优于PathMatch，SSD算法需要传输的信息最少。PathMatch 和 STwigMatch 传输的信息量较大，非常耗时;SSD算法采用DAG分解，可有效降低信息投递和查询响应时间。此外，对于大小大于 7 的模式图，STwigMatch 和 PathMatch 算法都超出了内存限制，导致查询过程缓慢。
Gao等[29]进一步提出了基于SSD的Stp（Q）算法，解决了SSD算法在数据图变化过程中超步进导致的结果不一致问题。对于图。 19 ，UpdateRation 表示数据图的更新率。实验结果表明，SSD算法的精度随着数据图或模式图变化程度的增加而降低。同时，采用Stp（Q）的SSD算法可以有效保证100%的准确率。

前面的讨论表明，单独使用基于探索的匹配会导致性能不佳。因此，可以设计一种基于连接和基于探索的组合方法来提高性能，使用基于连接的方法分解查询框架，并在匹配过程中使用基于探索的匹配方法。有效利用信息传递方法对形态图进行分解至关重要。一个好的分解方法将减少要传输的信息量，提高查询效率。同时，引入有效的算法来提高结果的准确性至关重要。
（3）基于仿真的匹配技术
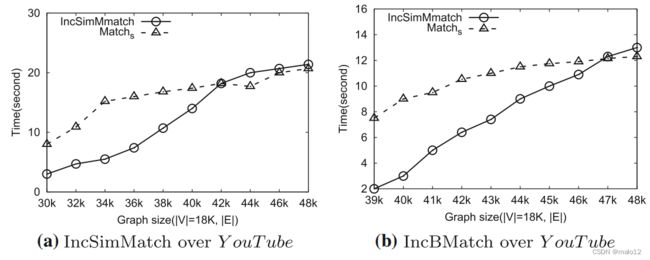
在[23]中，使用真实的YouTube和引文网络数据集，将IncSimBMatch算法与相应的批处理算法匹配和匹配算法进行比较。图20a结果表明，当添加或删除的边数不超过数据图中边数总数的40%时，增量算法的性能优于批处理算法。为我ncBMatch算法，如图20b所示当添加或删除的边数不超过数据图中边数总数的20%时，增量算法优于批处理算法。

[76]等人比较了所提出的剪枝算法D-IDS和IncBMatch算法。IncBMatch使用受限模拟对数据图进行了修剪，提供了les的结果s与模式图的结构相一致。同时，D-IDS算法通过二值模拟匹配得到的结果与模式图更加一致。试样分析结果表明，D-IDS算法可以将数据图的大小平均减少60%。对于直径较小的数据图，性能改进更大。效率对于直径更大的数据图，也得到了改善，但并不显著。Kao等人[41]将分布式增量算法与批处理算法进行了比较。实验results显示，在第12次更新后，增量算法的匹配率是批处理算法的3∼10倍，可以过滤出60%以上的无效更新出局。
综上所述，基于增量技术的连续子图匹配研究越来越广泛。通常，从三个角度来考虑算法的性能。第一种是设计一种增量算法，充分利用前面的匹配结果来过滤掉无效的更新。第二种是设计一种高效的增量子图匹配算法，以找到可能围绕新添加的边匹配结果的候选集。三是设计剪枝策略，进一步过滤掉匹配候选集中的无效结果。
不同的应用用途需要不同的近似方法。为了准确起见，基于连接的方法可以获得精确匹配的结果，这些结果适用于对图形拓扑有严格要求的应用。相比之下，基于连接的匹配技术会产生许多中间结果，从而导致效率降低。基于探索的方法会提高匹配效率，但精度会降低;因此，可以使用结合前两种方法的匹配方法来优化性能。此外，图形仿真可用于对拓扑结构没有严格要求的应用。一些扩展图仿真匹配方法可以获得与模式图具有较高相关性的匹配结果，从而弥补了基于连接的方法和基于探索的方法的不足。
（4）增量算法的综合对比
Kim等人[43]使用LSBenc评估了以数据为中心的表示（TurboFlux）与以查询为中心的表示（sj树）(直接计算方法（图流）的性能h数据集，用于[17]。实验使用了树和图形查询。在实验结果的比较中，评估了平均运行时间（M（g，q））和存储成本。
图21显示了在LSBench中的树形查询的性能结果。值得注意的是，与辅助数据结构的匹配优于直接计算方法。所注意到的查询大小较小的是基于平均运行时间的tter性能。此外，以数据为中心的表示优于以查询为中心的表示。在平均运行时间内，TurboFlux比SJ-tree好77.30 379无论查询大小为0.22次，图形流为515.01 1,275.68次，无论查询大小如何。这是因为SJ-tree使用连接操作生成了大量的部分解决方案。由于图形流使用t采用直接计算方法，没有产生任何中间结果；因此，TurboFlux只在存储成本上进行比较。SJ-tree显示了一个显著的存储成本问题lem.SJ-tree的平均存储成本明显大于TurboFlux，高达142.34倍。显然，涡轮通量可以有效地减少搜索空间。

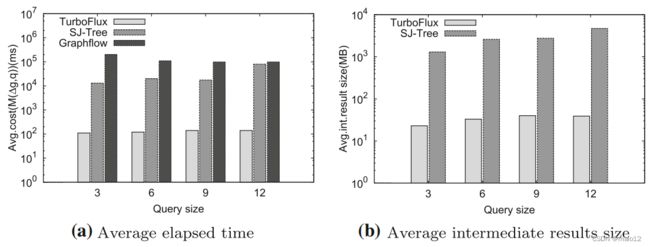
SJ 树存在明显的中间结果大小问题。其中，sj树中间结果的平均大小明显大于TurboFlux，达到142.34倍。显然，TurboFlux 可以有效地利用 DCG 来减少搜索空间。
从以上实验结果可以看出，保持中间结果可以提高性能。特别是，以数据为中心的表示具有最佳性能。TurboFlux 在处理不同的查询集、数据集和插入率时，始终显著优于最先进的方法。基于图的辅助数据结构可以帮助我们更快地跟踪受影响的顶点，并更轻松地获取它们。在未来的研究中，应考虑具有更高性能和更低功耗的新型辅助数据结构。
最近，Sun等[68]对连续子图匹配进行了深入研究。在[ 43 ]中，他们没有比较树形查询和图查询，而是将图查询分为稀疏图查询和密集图查询。他们发现，最新的算法并不能始终如一地优于旧算法，在某些情况下，直接计算增量方法的运行速度比具有辅助数据结构的增量方法更快。具体来说，（1）在树查询上，TurboFlux和SJ-Tree的运行速度比Graphflow快得多;（2）在稀疏图查询上，Graphflow的运行速度比TurboFlux快;（3）在密集图查询上，Graphflow总体优于TurboFlux;（4）如果在数据图中的稀疏区域更新边，则Graphflow的运行速度比TurboFlux快。

5.2 Content-based change

基于内容变化的连续子图匹配算法一般在查询时间和可扩展性方面进行比较。在[ 88 ]中，将Gradin与VF2、UpdAll、NaiveGrid和UpdNo算法进行了比较;VF2 是一种无索引子图匹配算法，UpdAll 将查询共享部署到多维搜索树中，NaiveGrid 是使用传统验证算法的网格索引，而 UpdNo 使用倒排索引。实验使用真实数据集BCUBE，该数据集由数据中心的网络架构组成，其中选取了3000个节点作为实验数据集。如图所示。 22、实验结果表明，Gradin算法的剪枝率和查询时间与UpdAll算法相似;然而，索引构建时间是 UpdAll 算法的 4 到 10 倍。同时，Gradin 算法的剪枝率是 UpdNo 算法的 10 倍，是 NaiveGrid 算法的 5 倍。Gradin 算法使用基于连接的匹配来加快图匹配过程，在这种情况下，它提供了最快的搜索速度。

主要用于数据中心的内容变化的连续子图匹配不像结构变化那样被广泛研究。一般从以下两个方面来考虑。首先，对于属性更新不频繁的应用，可以使用基于连接的匹配技术，类似于静态图匹配。其次，对于属性更新频繁的应用程序，可以采用基于探索的匹配方法，因为基于连接的匹配方法会产生大量的中间结果。

6 Application analysis of continuous subgraph matching technique

近年来，图数据被广泛用于描述现实世界中各种实体之间复杂且不断变化的关系。因此，与传统的静态图子图匹配技术相比，连续子图匹配技术的应用场景更加广泛。本节总结了连续子图匹配技术的实际应用。

6.1 Criminal behavior analysis

当前，贩毒、恐怖袭击等犯罪行为在世界范围内造成严重危害。通过将行为关系图建立为数据图，以人为节点，以活动关系为边，可以使用犯罪集团行为关系图来定义模式图。使用此模式图和动态数据图上的子图匹配技术，可以发现和预测潜在的犯罪行为。
例如，在动态图上使用了一种有限的模拟匹配技术来分析[23]中潜在的贩毒群体。如图23所示，其中p0为模式图，由节点表示嫉妒罪犯和代表他们之间的人口贩运的边缘。边缘上的边缘标签（AM、FW）的值为3，说明需要从AM开始满足传输约束在3跳范围内进行FW。基于模式图，通过在一个大规模的动态行为关系图中进行搜索和匹配，可以找到潜在的贩毒群体，提供了一个强有力的基础用于发现犯罪行为。据报道，美国著名的情报公司帕兰蒂尔也使用这种技术进行调查和分析具体情况。

6.2 Road network monitoring

城市道路交通监测是连续子图匹配的重要应用。城市路网可以用图形表示，其中交叉点用节点表示，路段用边表示。用户可以根据交通事故发生后的典型路况定义模式图，并将模式图与动态路网数据图进行匹配，实现对交通事故的实时监控。
以[66]中的路网监测为例，图。 24 A 表示交通事故后发生的典型路况，边缘的标签表示交通状况（拥堵或平稳）。在匹配过程中，需要满足时间的偏序关系，可以定义为如图所示的时间关系图。 如图24b所示，其中每个节点对应于图中的一条边。 24 一个。仅当模式图和数据图的子图与时域中的顺序匹配时，如图所示。 24 b，它们是否被视为最终匹配结果。每份道路交通报告都可以看作是对路网图数据的更新，更新的部分需要在图中所示的时间窗口内进行验证。 24个分类。图24 d、e表示不同时间点的路网数据图的两个快照，其中括号中的数字表示时间。通过事件模式图之间的子图匹配可以完成实时交通事故监测（图1）。 图24 a）和在不同时间动态变化的路网数据图（图24 a）和路网数据图（图24 a）和在不同时间动态变化的路网数据图（图24 a）和在不同时间动态变化的路网数据图（图2 24 d，e）。在本例中，图中的子图。 24 e 与模式图匹配。

6.3 Network security monitoring

随着互联网的快速发展，网络安全问题也变得更加严重。以[17]中的网络攻击监控为例，如图17所示。 图25显示了三种用户定义的网络攻击行为模式。图中，节点表示主机，边表示交互关系，例如登录时主机与用户之间的通信。通过攻击模式和流图之间的连续子图匹配，可以检测真实和潜在的网络攻击事件，以预测网络攻击行为。

6.4 Computational biology data analysis

在生物学中，分子结构可以用图形表示，为研究生物组织的结构和功能提供了重要依据。在蛋白质相互作用网络中，蛋白质与某些引起突变的酶发生反应。通过将已知的蛋白质网络模式与动态蛋白质相互作用网络相匹配，可以快速找到突变的蛋白质结构。例如，Bader等[12]通过计算蛋白质相互作用网络的连通性和中心性，并将结构与蛋白质相互作用网络的已知特性相匹配，发现具有大介数和小连通性的蛋白质是人类基因中的冗余蛋白质，该网络包含18,000个蛋白质（节点）和44,000个蛋白质相互作用（边缘）。这无疑为分析基因和蛋白质的功能提供了重要依据。

7 Future work

动态图作为一种应用广泛的数据模型，具有理论意义和广泛的应用前景;因此，动态图数据匹配的研究越来越受到学术界和产业界的关注。随着大数据的出现，数据规模越来越大，数据更新越来越频繁，数据之间的关系也越来越复杂。这无疑给连续子图匹配的研究和应用带来了新的挑战和机遇。我们提出了以下有前途的未来方向清单。
分布式并行图流程 面对图数据规模的快速增长，大规模图数据匹配技术的可扩展性有待提高。因此，必须研究基于主流分布式并行图处理框架系统（如Pregel和Giraph）实现图匹配并行分布式处理的方法。这些主流的分布式并行图处理框架系统通常采用以顶点为中心的处理模式。每个节点作为框架中的基本计算单元，存储和处理图数据的一个分区，而在以块为中心的模型中，基本计算单元是一个块，用于存储和处理数据图的连接子图。两种分布式并行图处理模型各有优缺点，研究人员可以根据自己的应用需求应用最适合的模型。
增量算法 对于频繁更新的图数据，基于快照的匹配方法并不能满足连续子图匹配的实时性需求。因此，必须研究基于动态图特征的高效匹配方法和查询优化策略。越来越多的增量子图匹配算法被提出，这些算法使用不同的辅助数据结构[43]，或过滤策略[54]或匹配顺序优化策略[67]。为了更好地进行连续子图匹配，我们主要关注的仍然是增量算法的构建，并采用一些优化策略来提高匹配效率。
匹配技术 基于连接的匹配技术是实现连续子图匹配的有效方法。然而，从模式图或数据图中提取高质量的特征是该技术面临的核心问题之一。一方面，为了避免数据图更新失败，目前的研究一般选择使用简单的子图，如单边子图或双边子图作为数据图的特征。然而，这种简单的子图不具有很强的可识别性，导致中间匹配结果较多，子图连接阶段的处理成本增加。因此，提取更多可识别特征并设计高效的特征维护方案应是未来研究的重点。另一方面，基于探索的连续子图匹配方法有其优点，但匹配结果的精度较低。为了解决这一问题，可以进一步研究基于探索和基于连接的连续子图匹配技术。这些研究应侧重于最佳地利用各自技术的优点来弥补不足。一些研究集中在模拟匹配技术上，该技术避免了复杂的子图同构匹配计算。对这一主题的进一步研究将是有利的。此外，基于特定需求设计图匹配相似度度量模型，开发更高效的图匹配近似算法是未来研究的考量。
模式演化 目前关于连续子图匹配的研究大多是针对模式图保持不变、数据图随时间变化的情况。然而，在现实生活中，模式图的变化也很常见。例如，在网络安全中，病毒经常变异，网络攻击模式不断演变;在计算生物学中，蛋白质变性和病毒突变也偶尔发生。[ 86 ] 研究了数据图不变，但模式图动态变化时图模式匹配的增量算法。Zhang等[84]将网络流量建模为一个大图，将攻击行为建模为演化模式图。然后通过连续子图匹配可以检测到异常攻击。因此，研究人员可以探索这些领域所需的增量处理技术;此外，还可以探索适应模式图和数据图变化的技术，以拓展连续子图匹配技术的应用领域。
多查询答案 大多数现有的连续子图匹配研究一次只处理一个查询。但是，由于图形的规模很大且不断发展，因此使用多个查询来监视和检测感兴趣的连续模式更为实用。Pugliese等[59]利用多个查询图的合并视图来增量更新结果。Zervakis等[83]设计了一种查询图聚类算法来处理大量的连续查询。Mhedhbi等[52]提出了一个通用的贪婪优化器，用于在连续查询的多个实例之间共享计算。尽管存在一些最先进的方法，但如何减少空间消耗和时间消耗，以及如何快速检测受更新影响的查询仍然是主要问题。所有这些方法都可以通过更好的过滤策略和匹配顺序或更高效的辅助数据结构来进一步改进。

8 Conclusion

在本文中，我们在 2009 年至 2020 年间发表的 20 篇研究文章中广泛研究了动态图上的连续子图匹配主题。我们首先根据不同的问题指标对这些文章进行分类。然后，基于动态图的不同更新方法，回顾和讨论了两种不同类型的连续子图匹配方法。此外，还讨论了每种算法的性能。最后，指出了未来的研究方向和主要挑战。综上所述，我们的调查概述了有关连续子图匹配的最新研究成果，这将使研究人员有一个透彻的了解。